36

2. Линейные электрические цепи с источниками периодических негармонических воздействий

Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону. На рис. 2.1 представлена такая кривая, период повторения которой Т. Эта кривая может быть описана функцией

, (2.1)

где n=0, 1, 2 и т.д.

П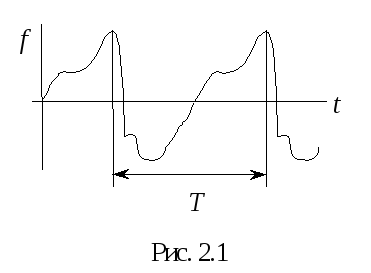ричины появления несинусои­дальных сигналов:

1. Источник тока или источник напряжения генерируют несинусоидальный ток или несинусоидальную ЭДС, а все элементы цепи (R, L, C) линейны, т.е. от величины тока не зависят.

2. Источник тока или источник напряжения генерируют синусоидальный ток или синусоидальную ЭДС, но один или несколько элементов цепи нелинейны (вентиль, электрическая дуга, катушка со стальным магнитопроводом).

3. Воздействие периодических помех на синусоидальный сигнал.

4. Использование генераторов сигналов специальной формы (пилообразной, ступенчатой, прямоугольной) в автоматике, вычислительной технике, в различных устройствах радиосвязи.

Существует два пути расчета линейной электрической цепи при воздействии сигналов такой формы:

1. Применение специальных математических приемов, отражающих состояние цепи в каждый момент времени, что приводит к сложной системе дифференциальных уравнений. Поэтому он не нашел применения в инженерных расчетах.

2. Сведение сложной задачи к совокупности более простых и применение известных методов расчета их с учетом особенностей воздействующего сигнала.

Известно, что любая периодическая несинусоидальная функция f(t) с периодом 2, удовлетворяющая условиям Дирихле, т.е. имеющая на всяком конечном интервале времени конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть разложена в тригонометрический ряд, т.е. быть представлена в виде суммы гармонических составляющих – ряд Фурье. Все периодические сигналы, используемые в электротехнике, удовлетворяют условиям Дирихле, поэтому проводить проверку на выполнение условия Дирихле нет необходимости.

Гармонический ряд в тригонометрической форме имеет вид:

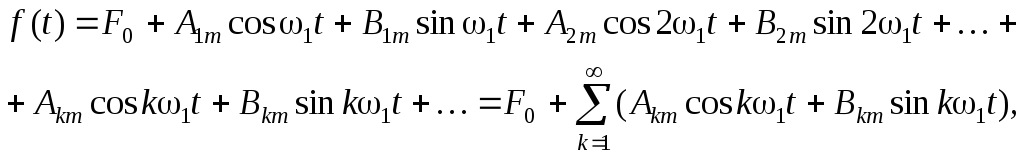( 2.2)

где –постоянная составляющая или нулевая гармоника, равная среднему значению функции за период;

A_km и B_km  – амплитуды косинусоидальных и синусоидальных составляющих.

Как известно из курса математики, коэффициенты ряда Фурье ,AkmиBkm определяются с помощью формул:

Сумма косинусоид и синусоид, выражаемая формулой (2.2), может быть представлена в виде суммы только одних синусоид с соответствующими начальными фазами, так называемая амплитудно-фазовая форма:

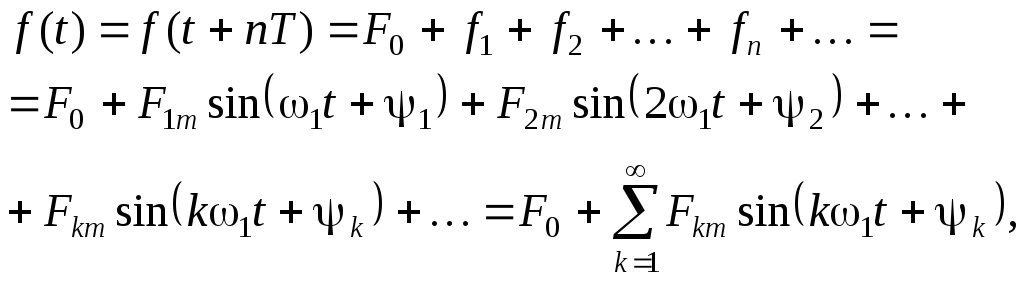(2.3)

где F₀ – постоянная составляющая;

f₁ – основная синусоида, или первая гармоника;

f₂, …, f_k – высшие гармоники;

F_km – амплитуда k – ой гармоники;

_k – начальная фаза k – ой гармоники;

₁ – частота повторения первой (основной) гармоники, ;

Т – период несинусоидальной периодической функции.

Гармоники, для которых k – нечетное число, называют нечетными, для которых k – четное число, – четными.

Поскольку

,

то из сравнения двух форм записи гармонического ряда (2.2) и (2.3) имеем

(2.4)

Соотношения (2.4) позволяют переходить от ряда Фурье в виде (2.3) к виду (2.2). Обратный переход осуществляется по формулам

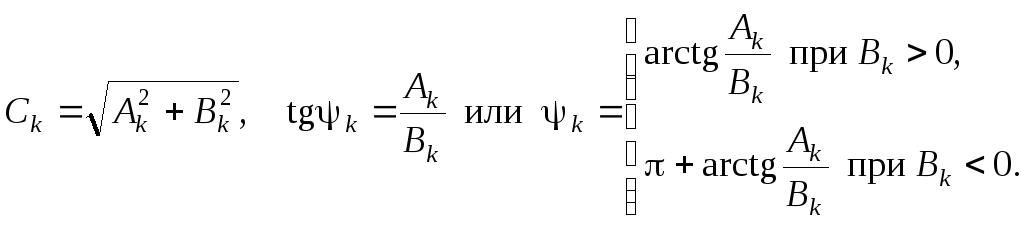. (2.5)

В общем случае ряд Фурье содержит бесконечное число членов. Однако обычно он быстро сходится и достаточно взять небольшое число гармоник для получения требуемой точности.

Существуют приборы, именуемые гармоническими анализаторами, позволяющие определять коэффициенты A_k и B_k или механически по заданному графику кривой f(t), или электрически путем подачи на зажимы прибора исследуемого несинусоидального напряжения.

Периодические несинусоидальные функции, описывающие изменения токов или напряжений в электрических цепях, обычно обладают каким-либо видом симметрии, и это облегчает разложение их в ряд Фурье.

В ряде случаев целесообразно представить ряд Фурье в комплексной форме:

, (2.6)

где

. (2.7)

В выражении (2.6) каждой k–й гармонике отвечает сумма двух сопряженных членов (при q = + k и при q = – k), равная удвоенной вещественной части каждого из этих членов:

. (2.8)

Обозначив , имеем

, (2.9)

где .

Таким образом, величина

(2.10)

представляет собой комплексную величину k-ой гармоники

, (2.11)

где .

Совокупность амплитуд всех гармоник данной функции может рассматриваться как дискретный спектр этой функции. Его можно представить на графике в виде спектра значений амплитуд и спектра значений фаз. По оси абсцисс откладываем значения, равные частотам гармоник. Для каждой частоты гармоник откладываем от оси абсцисс параллельно оси ординат отрезки, длины которых равны амплитудам A_kили начальным фазам_k гармоник. При этомA_k > 0, а_k может быть как положительным, так и отрицательным. Такие характеристики носят названиедискретных спектров илидискретных частотных характеристик – соответственноамплитудно-частотной ифазо-частотной характеристик.

При построении спектра периодического сигнала по оси абсцисс откладывают кратные основной частоте значения частот гармонических составляющих. Обратим внимание на то, что чем больше период функции f(t), тем плотнее расположены спектральные линии и соответственно меньше значения амплитуд гармонических составляющих. Разумеется, в конкретных случаях те или иные частотные составляющие спектра сигнала могут отсутствовать, но составляющих, частота которых не кратна основной частоте, спектр содержать не может.

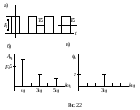
Пример. Определим спектр периодической последовательности прямоугольных импульсов амплитудыF₀ с длительностью, раной половине периода,T/2 (рис. 2.2, а). Аналитическое выражение временной зависимости рассматриваемого сигнала на периоде имеет вид

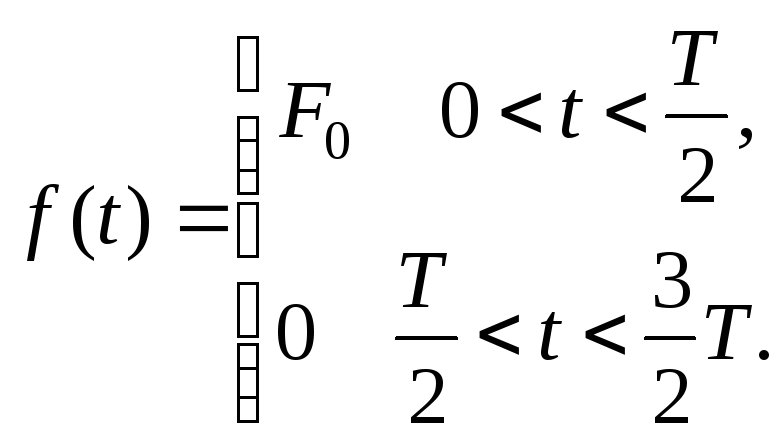
Если за начало отсчета выбрать начало координат, то функция обладает четной симметрией и содержит только косинусные составляющие с коэффициентами A_k. Определим амплитудуk-й гармоники

.

Отсюда

Найденные коэффициенты позволяют записать разложение Фурье:

Спектры амплитуд и фаз принимают следующие значения:

и изображены на диаграммах рис. 2.2,б и 2.2 в.