
- •Введение
- •Понятие модели
- •Лекция 2 Математическое моделирование однофазных потоков
- •Лекция 3 Математическое моделирование теплообменных процессов
- •Температурное поле
- •Основы теплового расчета
- •Проектный расчет теплообменного аппарата
- •Проверочный расчет теплообменного аппарата
- •Математические модели теплообменников
- •Теплообменник типа «перемешивание-перемешивание»
- •Теплообменник типа «перемешивание-вытеснение»
- •Теплообменник типа «вытеснение-вытеснение»
- •Постановка задачи
- •Для прямотока
- •Для противотока
- •Тепловой баланс теплообменника: для прямотока
- •Для противотока
- •Варианты заданий для расчета теплообменника
- •Лекция 4 Моделирование кинетики химических и ферментативных реакций
- •Постановка задачи
- •Обратная задача кинетики
- •5.2. Методические указания по практической части.
- •3.4.1. Ингибирование ферментативных реакций
- •Математическое моделирование биОлогической очистки сточных вод в аэротенке
- •Аэротенк
- •Лекция 6 Автоматизированная оценка степени загрязнения окружающей среды от газовых выбросов
Для прямотока
![]()
![]()
Здесь: Т и Тх– текущие значения температур,
соответственно горячего и холодного
потоков,0С; Х – текущее значение
длины теплообменника, м; КТ –
коэффициент теплопередачи от горячего
потока хладоагенту, ккал / (м2час);F= π.d– поверхность теплообмена на единицу
длины, м2;d– диаметр
внутренней трубы, м;V,Vx
– объемные скорости горячего и
холодного потоков, м3/с; Сp,Cpx
– теплоемкость горячего и холодного
потоков, ккал / (кг. 0С);![]() ,
,![]() - плотности горячего и холодного потоков,
кг/м3.
- плотности горячего и холодного потоков,
кг/м3.
Начальные условия:
 Х
= 0 ТХ=0 = Т0
Х
= 0 ТХ=0 = Т0
 Т
= Т0 или
Т
= Т0 или
Тх= Тх0 ТХХ=0 = Тх0
Здесь: Т0, Тх0 - начальные значения температур горячего и холодного потоков, соответственно
Для противотока
![]()
![]()
Краевые условия:
 Х
= 0 ТХ=0 = Т0
Х
= 0 ТХ=0 = Т0
 Т
= Т0 или
Т
= Т0 или
Тх= ТхК ТХХ=L = Тх0
Краевые условия получены из уравнения теплового баланса:
![]() (Т0- ТК) =Vx
(Т0- ТК) =Vx![]() х(ТxK-
Тx0), откуда
получаем формулу для расчета конечной
температуры холодного потока:
х(ТxK-
Тx0), откуда
получаем формулу для расчета конечной
температуры холодного потока:
ТхК
= Тх0 +![]() (Т0- ТK)
(Т0- ТK)
Тепловой баланс теплообменника: для прямотока

 dX
dX
ρ


 ,
Ср,V,TºTºTº+dTρ, Ср,V,TK
,
Ср,V,TºTºTº+dTρ, Ср,V,TK
ρ x,CpX,VX,TXºTX TX+dTXρx,CpX,VX,TXK
x,CpX,VX,TXºTX TX+dTXρx,CpX,VX,TXK



для горячего потока
ρ·Cp·V·T-ρ·Cp·V(T+dT) +KT·πd(TX-T)dX =0
ρ·Cp·V·T-ρ·Cp·V·T-ρ·Cp·V·Dt+KT·πd(TX-T)dX =0
![]()
для холодного потока
ρX·CpX·VX·TX - ρX·CpX·VX(TX+dTX) + KT·πd(T-TX)dX =0
ρX·CpX·VX·TX - ρX·CpX·VX(TX+dTX) + KT·πd(T-TX)dX =0
ρX·CpX·VX·TX - ρX·CpX·VX·TX - ρX·CpX·VX·dTX + KT·πd(T-TX)dX =0
![]()
Для движущей силы : в случае горячего потока внешней является
ТХ; а в случае холодного потока – внешней является Т
ρ·Cp·V·T– количество тепла, вносимого потокомVв элементарный объемdVвнутренней трубы
ρ·Cp·V(T+dT) – количество тепла, уносимого потокомVи элементарный объемdVвнутренней трубы
q=KT·πd(TX-T)dX - количество тепла, переданного за счет теплопередачи через поверхностьS=πddXвнутренней трубы
Для противотока
dX
ρ




 ,
Ср,V,TºTT+dTρ, Ср,V,TK
,
Ср,V,TºTT+dTρ, Ср,V,TK
ρx,CpX,VX,TXKTX TX+dTXρx,CpX,VX,TXº




для горячего потока
ρ·Cp·V·T-ρ·Cp·V(T+dT) +KT·πd(TX-T)dX =0
ρ·Cp·V·T-ρ·Cp·V·T-ρ·Cp·V·Dt+KT·πd(TX-T)dX =0
![]()
для холодного потока
ρX·CpX·VX(TX+dTX) - ρX·CpX·VX·TX + KT·πd(T-TX)dX =0
ρX·CpX·VX·TX - ρX·CpX·VX·TX + ρX·CpX·VX·dTX + KT·πd(T-TX)dX =0
![]()
а) прямоток:
dX
ρ





 ,
Ср,V,TºTºqTº+dTρ, Ср,V,TK
,
Ср,V,TºTºqTº+dTρ, Ср,V,TK


d
ρ
 x,CpX,VX,TXºTX TX+dTXρx,CpX,VX,TXK
x,CpX,VX,TXºTX TX+dTXρx,CpX,VX,TXK




б) противоток:
dX
ρ





 ,
Ср,V,TºTqT+dTρ, Ср,V,TK
,
Ср,V,TºTqT+dTρ, Ср,V,TK

 d
d
ρ
 x,CpX,VX,TXKTX TX+dTXρx,CpX,VX,TXº
x,CpX,VX,TXKTX TX+dTXρx,CpX,VX,TXº




Варианты заданий для расчета теплообменника
|
№
|
V, м3/ч |
VX, м3/ч |
Cp, ккал кг·0С |
CpX, ккал кг·0С |
ρ, кг/м3 |
ρX, кг/м3 |
Tº, ºС |
TXº, ºС |
TK, ºС |
d, м |
KT, ккал м2·ч |
|
1 |
40 |
70 |
1 |
1 |
1000 |
1000 |
120 |
20 |
80 |
0,2 |
1000 |
|
2 |
50 |
80 |
1 |
1 |
1000 |
1000 |
100 |
30 |
70 |
0,2 |
1000 |
|
3 |
40 |
90 |
1 |
1 |
1000 |
1000 |
110 |
20 |
80 |
0,25 |
1000 |
|
4 |
30 |
60 |
1 |
1 |
1000 |
1000 |
120 |
20 |
70 |
0,15 |
1000 |
|
5 |
40 |
80 |
1 |
1 |
1000 |
1000 |
110 |
25 |
75 |
0,1 |
1000 |
|
6 |
50 |
90 |
1 |
1 |
1000 |
1000 |
130 |
30 |
80 |
0,3 |
1000 |
Р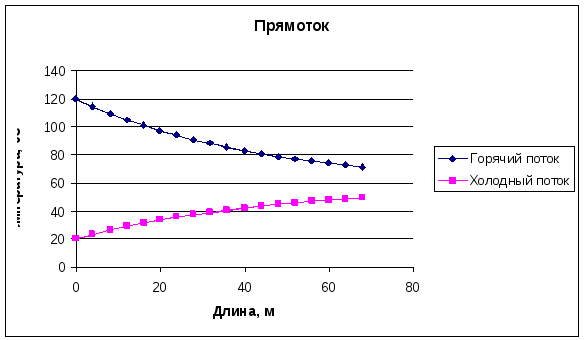
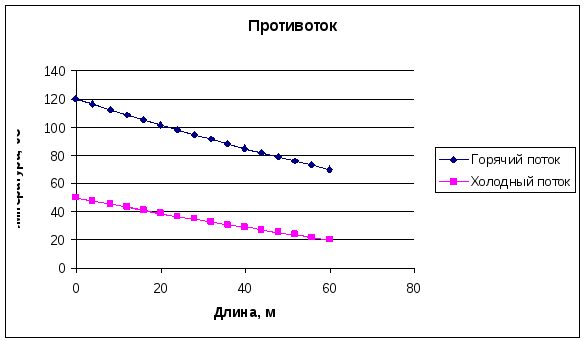 ис.
5. Профиль изменения температур горячего
и холодного потоков
ис.
5. Профиль изменения температур горячего
и холодного потоков
