
РГР_1_2011
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н.ТУПОЛЕВА КАЗАНСКИЙ
Аристова Н.С., Одиноков А.Ю., Петрушенко Ю.Я.
ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ ДЛЯ СТЕРЖНЕЙ И РАМ
(Учебное пособие по выполнению расчетно-графических работ)
Казань 2007
УДК 620.10(077)
Построение эпюр внутренних силовых факторов для стержней и рам. Учебное пособие по выполнению расчетно-графических работ / Н.С. Ари- стова, А.Ю. Одиноков, Ю.Я. Петрушенко; - Казан. гос. техн. ун-т, Казань, 1998. 61с.
Рассмотрены вопросы построения эпюр внутренних силовых факторов при изгибе статически определимых балок. Решение осуществляется непосредственно из уравнений равновесия, что позволяет проследить аналогию с задачами теоретической механики. Содержит сборник заданий на выполнение расчетно-графических работ. Пособие предназначено для студентов всех специальностей, изучающих этот раздел сопротивления материалов.
- 3 -
ВВЕДЕНИЕ
В учебном пособии рассматривается применение принципов статики на одном из начальных этапов прочностного анализа, при построении эпюр внутренних силовых факторов (ВСФ) в стержнях, рамах и кривых брусь- ях [1-3]. В качестве расчетной схемы (модели), для элементов рассматривае- мых конструкций принят стержень (брус, балка), т.е. тело, два размера кото- рого значительно меньше третьего.
Иначе говоря, рассматривается способ нахождения суммарных сил и моментов, которые передаются в стержнях от сечения к сечению. Очень многие реальные конструкции могут быть представлены с той или иной сте- пенью точности как стержни, это балки перекрытия зданий и крылья самоле- тов, другие могут рассматриваться как криволинейные стержни или рамы, например, подмоторные рамы у самолетов и вертолетов, шпангоуты фюзе- ляжей и т.п.
Как стержни могут рассматриваться лопатки турбин и лопасти воз- душных винтов. Эти детали конструкций отличается не только сложно- стью геометрии поперечного сечения, но и сложным по физической при- роде и характеру действия внешним нагружением. В число нагрузок ло- патки входят вес самой лопатки, инерционные и аэродинамические силы, тепловое поле и т.д.
Простейшей расчетной схемой лопатки является консольная балка (консольной называется балка, один торец которой свободен, а второй – за- щемлен). Такая же расчетная схема может быть использована для со- вершенно других конструкций, из других областей техники. Например, кон- сольная балка может являться расчетной схемой резца.
Начальный этап прочностного расчета (построение эпюр ВСФ) для обеих конструкций выполняется совершенно аналогично, хотя нагружение лопатки все же много сложнее, чем у резца, соответственно и более трудо- емким является построение эпюр ВСФ для лопатки.
Далее в пособии мы не будем останавливаться на вопросах выбора рас- четной модели конструкции и схематизации ее нагружения, т.к. эти вопросы являются совершенно самостоятельными разделами прочностного анализа. Научившись строить эпюры для этих относительно простых расчетных моде- лей, студент, мы надеемся, сможет сделать это и для более сложных случаев.
-4 -
1.ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ В СТЕРЖНЯХ. ОБЩИЕ ПОЛОЖЕНИЯ
Внастоящем учебном пособии рассматривается построение эпюр внутренних силовых факторов (ВСФ) в стержнях (брусьях), для которых действующие на них внешние силы лежат в одной плоскости (плоскости чертежа), а внешние моменты вращают стержень относительно оси, пер- пендикулярной этой плоскости.
Считаются справедливыми традиционные допущения, принятые в ме- ханике деформирования линейно-упругих тел [1-2], в том числе и гипотеза о малости перемещений и деформаций, которая позволяет при определении
сил рассматривать равновесие деформируемой конструкции и ее частей в недеформированном состоянии. Кроме того, учет данной гипотезы позволя- ет, при соответствующем выборе системы координат, разделить задачи о растяжении-сжатии и об изгибе стержней, а общее напряженно-дефор- мированное состояние может быть найдено в соответствии с принципом су- перпозиции простым сложением полученных решений.
Предполагается, что стержень имеет необходимое и достаточное число опор, обеспечивающих ее неподвижность в пространстве (плоскости чер- тежа), что позволяет определить ВСФ в любом сечении стержня с помощью только уравнений статики (уравнений равновесия). Такие стержни называ- ются статически определимыми.
За ось стержня принимается линия, проходящая через центры тяже- стей ее поперечных сечений.
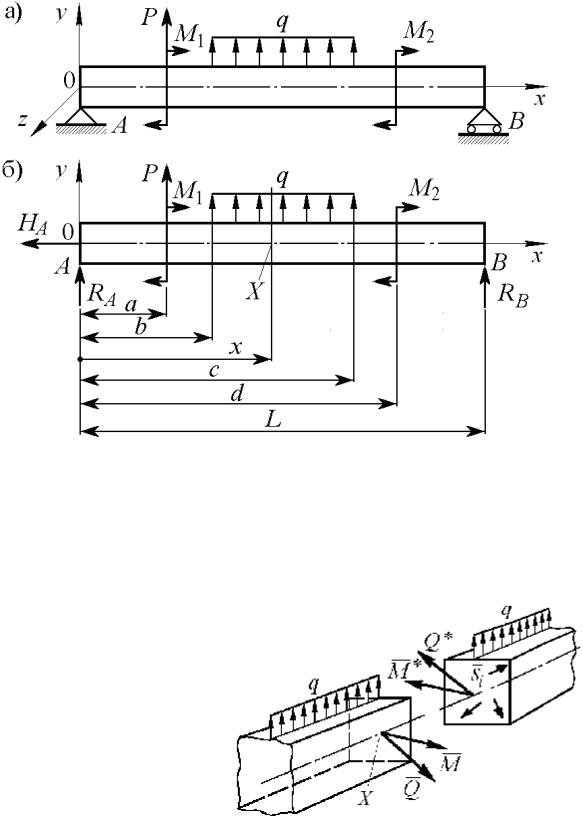
Условимся относить стержень к правой системе декартовых координат xyz (рис. 1.1.а), начало которой совмещено с ее левым торцевым сечением, а ось x направлена вдоль оси стержня и проходит через центры тяжести попе- речных сечений, которые считаются лежащими на одной прямой. Плоскость x0y совпадает с плоскостью чертежа. В дальнейшем рассматривается пре- имущественно задачи для плоскости x0y. Полагаем, что балка, изображенная
на рис. 1.1.а нагружена сосредоточенной силой P, сосредоточенными момен- тами M1, M 2 и распределенной внешней нагрузкой q. Как известно, балками
называются стержни, работающие на изгиб.
Отделим балку от опор, действие которых на нее заменим реактивными усилиями RA , H A и RB (рис. 1.1,б). В силу того, что исходное состояние
балки является равновесным, для определения опорных реакций использу- ются уравнения плоского равновесия для абсолютно твердого (жесткого) те-
ла (после вычисления опорных реакций необходимо выполнить проверку пра-
- 5 -
вильности их определения). Заметим, что при отсутствии активных горизон- тальных сил опорная реакция H A =0.
Рис. 1.1
Таким образом, действующая на балку система внешних сил и момен- тов является известной, а балка при этом находится в равновесии.
От внешней нагрузки между материальными точками внутри балки возникают дополнительные силы взаимодействия. Будут они и между точка- ми двух сторон любого из по- перечных сечений балки. На- пример, поперечного сечения,
проведенного в точке оси X с координатой x, (рис. 1.1). Си- лы Si , возникающие в этом се-
чении, изображены на рис.1.2. .
Приводя систему сил Si мето-
дами теоретической механики к центру тяжести поперечного се- Рис. 1.2 чения (точке, через которую

- 6 -
проходит ось стержня), получим главный вектор Q (Q ) и главный момент
M (M ). Звездочкой обозначены величины, приложенные к правой стороне сечения. (Следует заметить, что для плоского изгиба балки, изображенной на рис. 1.1, главный момент M перпендикулярен плоскости x0y, а главный век- тор Q лежит в ней, на рис. 1.2 представлен более общий случай, который рассмотрен в [1]). В соответствии с законом Ньютона о действии и противо- действии усилия, приложенные к левой стороне сечения, численно равны усилиям, приложенным к правой стороне сечения, но противоположно нап- равлены, т.е. в векторной форме справедливы равенства:
|
|
= − |
|
, |
|
|
= − |
|
. |
(1) |
|
|
|
|
M |
M |
|||||||
Q |
Q |
||||||||||
Проекции (составляющие) |
главного вектора |
|
и главного момента |
||||||||
Q |
|||||||||||
M на оси x, y, z представляют собой c точностью до знака внутренние си- ловые факторы в поперечных сечениях балки. В плоской задаче только три проекции векторов Q и M отличны от нуля. Это две составляющие главно- го вектора Q силы по осям x и y, которые обозначим Qx (x) и Qy (x), и одна составляющая главного момента M z (x). В плоских задачах эти величины будем еще для краткости обозначать соответственно N(x), Q(x), M(x), опус- кая индексы, указывающие ось. Каждая из величин N(x), Q(x) и M(x) в об- щем случае может изменяться от сечения к сечению, что подчеркивается тем, что в круглых скобках указывается функциональная зависимость от координаты x.
Аналогично самим векторам, составляющие векторов Q и M правой
стороны сечения также численно равны соответствующим составляющим векторов Q и M , но противоположно им направлены (рис. 1.3).
Внутренние силовые факторы N(x), Q(x) и M(x) могут быть найдены из
Рис. 1.3
условия равновесия левой части стержня, а равные им величины N (x), Q (x) и M (x) – из условия равновесия правой части. Действительно, на плоскости мы имеем три независимых условия равновесия и по три неиз- вестных величины входят в нагрузку каждой из частей. В рассматриваемом

- 7 -
случае, когда отсутствуют внешние силы, действующие вдоль оси балки (рис. 1.1), N (x) ≡ 0, что следует из уравнения равновесия для проекций всех
внешних сил на ось x:
k
åPxi = 0 = N(x) , откуда N (x) ≡ 0.
i=1
Нетрудно видеть, что в сумму проекций всех сил на ось y войдет для каждой из частей балки только одна неизвестная сила в сечении – Q(x) (или Q (x), если рассматривается равновесие правой части балки), которая может
быть легко найдена из этого уравнения
n |
|
n-1 |
|
åPyi |
= 0 |
= åYi − Q(x) . |
|
i=1 |
|
i=1 |
|
n-1 |
|
|
|
Расписав сумму сил åYi , |
приложенных |
к левой части балки |
|
i=1 |
|
|
|
(см. рис. 1.3), получим |
|
|
|
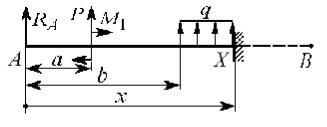
RA + P + q(x − b) − Q(x) = 0 |
(2) |
||
откуда следует, что
Q(x) = RA + P + q(x − b) .
Составим далее для левой части балки уравнение равновесия для мо- ментов относительно оси, перпендикулярной плоскости чертежа и про- ходящей через точку X (рис. 1.3), в которой ось балки пересекает рассматри- ваемое сечение. Учитывая силовые факторы, приложенные к балке слева от сечения, мы получим уравнение, содержащее лишь одну неизвестную ве- личину M(x) (или M (x), если рассматривается правая часть)
m |
m-1 |
åM X j = 0 |
= åM X j + M (x) . |
j=1 |
j=1 |
Положительным, как и в курсе теоретической механики, при составле- нии уравнений равновесия в плоской задаче считаем момент, вращающий выделенную часть балки против часовой стрелки. Тогда, расписав для левой части балки, изображенной на рис. 1.3, сумму моментов внешних сил, полу-
чим уравнение
− R |
|
x − P(x − a) - M1 |
− q(x - b) |
x - b |
+ M (x) = 0 , |
(3) |
A |
|
|||||
|
|
2 |
|
|
||
из которого следует, что
M (x) = RA x + P(x − a) + M1 + q (x -2b)2 .
- 8 -
Заметим еще, что для отыскания внутренних силовых факторов ис- пользованы именно эти три уравнения равновесия (т.е. сумма проекций сил на ось стержня, на перпендикуляр к оси и сумма моментов относительно точки X оси), поскольку в каждое из них вошла только одна неизвестная ве- личина внутреннего силового фактора в сечении.
Нетрудно видеть, что определение внутренних силовых факторов в се-
чениях в принципе ничем не отличается от нахождения опорных реакций для той же балки, но имеющей защемление в рассматриваемом сечении (рис. 1.4). Это и понятно. Ведь любая часть балки является, по сути, опорой, аналогичной защемлению, для ос-
тальной ее части.
Но все же задача определения внутренних силовых факторов в поперечном сечении несколько сложнее задачи определения опор- ных реакций.
Одна из сложностей заключается в том, что из равновесия левой части стержня определяются силовые факторы N(x), Q(x) и M(x), а из равновесия правой части – противоположно им направленные N (x), Q (x) и M (x) (рис. 1.3). Таким образом, в задаче в данном случае существуют три пары величин, отличающихся только знаком (направлением). Для того чтобы сде- лать задачу определения внутренних силовых факторов однозначной, в каче- стве искомых величин принимают только силы и моменты, действующие с правой части стержня на левую: N(x), Q(x), M(x), которые называют внутрен-
ними силовыми факторами в сечении. Выбирают именно эти величины, а не парные им, поскольку они действуют на площадке, из которой ось x исходит. Это положительная площадка.
Величина N(x) носит название внутренней осевой силы, Q(x) – внут-
ренней перерезывающей силы, M(x) – внутреннего изгибающего момента
(название факторов соответствует воздействию, которое оказывает каждый из них на балку). Положительное направление N(x), Q(x), M(x), действующих с правой отсеченной части стержня на левую, может быть, вообще говоря, выбрано произвольно. В сопротивлении материалов их положительные на- правления принято брать такими, как они показаны для левой части рис. 1.3.
Для того чтобы из равновесия правой части стержня получить те же значения внутренних силовых факторов, что и найденные из равновесия ее левой части следует, очевидно, в качестве положительных величин для пра- вой части принять величины, направленные противоположно N(x), Q(x),
- 9 -
M(x). Получается, что положительные направления при рассмотрении равно- весия правой части следует принимать такими, как N (x), Q (x) и M (x) на рис. 1.3. Это позволяет автоматически учесть знак минус в форму-
лах (1, стр. 6).
Таким образом, составляя уравнения равновесия для отыскания ВСФ,
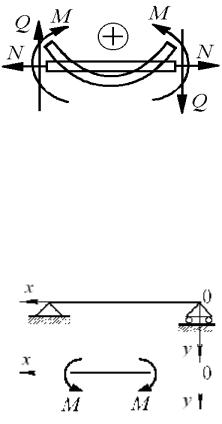
следует эти неизвестные силовые факторы изображать в положительном направлении, причем эти направления для левой и правой части стержня противоположны (рис. 1.5). Рис. 1.5 представляет собой правило знаков со- противления материалов для ВСФ плоской задачи.
Словами это правило формулируется следующим образом: осевые си-
лы положительны, если они вызывают растяжение стержня (направлены от сечения), перерезывающие силы положительны, если они направлены по часовой стрелке относительно рассматриваемой части стержня, а изги- бающие моменты положительны, если они сжимают ее верхние волокна, т.е. часть, расположенную в первой полуплоскости (положительной чет-
верти) системы координат (рис. 1.5). |
|
Вполне очевидно, что использованные на- |
|
ми понятия: левая и правая часть стержня, вер- |
|
хние и нижние волокна имеют смысл только по- |
|
сле задания для стержня соответствующей сис- |
|
темы координат. Напомним, что начало правой |
|
системы координат по умолчанию расположено |
Рис. 1.5 |
на левом торце стержня, ось x направлена слева |
направо, направление второй оси y в правой системе координат получается поворотом на 90° против часовой стрелки
Если стержень отнести к правой системе координат с началом в пра- вом торцевом сечении (рис. 1.6), то, конечно, "верхние волокна" стержня бу-
дут располагаться снизу и тогда положительны- |
|
|
ми будут моменты, изображенные на рис. 1.6. |
|
|
Но для балки такое расположение системы ко- |
|
|
ординат принимается редко. |
|
|
Приведенные выше рассуждения, позво- |
|
|
ляющие определить внутренние силовые факто- |
|
|
ры в произвольном сечении стержня, называют |
|
|
методом сечений. Кратко эти рассуждения |
Рис. 1.6 |
|
можно сформулировать в виде следующего ал- |
||
|
||
горитма. |
|
-10 -
1.Разрезаем мысленно стержень поперечным сечением в точке оси, где мы хотим определить внутренние силовые факторы.
2.Отбрасываем одну из частей стержня. Лучше отбрасывать ту ее часть, к которой приложено больше силовых факторов. Важно, однако, что- бы все внешние силовые факторы, в том числе и опорные реакции, действу- ющие на остающуюся часть стержня, были известными.
3.Заменяем действие отброшенной части стержня на остающуюся не- известными внутренними силовыми факторами (силами и моментами), кото-
рые прикладываем в выбранном сечении в положительном направлении в соответствии с принятым для ВСФ правилом знаков сопротивления мате- риалов.
4.Записываем для выделенной части стержня уравнения равновесия, из которых находим внутренние силовые факторы в сечении.
Для облегчения запоминания пунктов метода сечений его называют методом РОЗУ по первым буквам слов: разрезаем, отбрасываем, заменяем, уравнения. Говорят: "Применим РОЗУ".
Заметим, что силы и моменты между поперечными сечениями рассчи- тываемого стержня (или балки) мы всегда в сопротивлении материалов на- зываем внутренними, хотя, конечно, для рассматриваемой части стержня они
сточки зрения теоретической механики являются внешними. Кроме того, укажем, что при нахождении ВСФ применяются, таким образом, два правила
знаков. Одно обязательное правило знаков сопротивления материалов для ВСФ. Второе необязательное в данном случае правило знаков теоретиче- ской механики, согласно которому при записи уравнений равновесия (на- пример, уравнений (2) и (3)) составляющие в сторону соответствующей оси берутся со знаком плюс, а противоположно оси – со знаком минус, момент против часовой стрелки принимается со знаком плюс, по часовой – минус.
В практических расчетах часто бывает необходимо знать ВСФ во всех сечениях, в этом заключается еще одна сложность определения ВСФ. Каза- лось бы, что эта трудность легко преодолевается введением в уравнение пе- ременного параметра – координаты x, что дает возможность записать ис- комые величины как функции координаты x. Но оказывается, что при нали-
чии сосредоточенных сил затруднительно представить соответствующие функции N(x), Q(x) и M(x) в виде одного выражения сразу для всего стержня. Это приходится делать для отдельных его участков.
Эти функциональные зависимости принято изображать в виде графи- ков, построенных непосредственно на оси стержня и называемых эпюрами. Эпюры удобны тем, что дают наглядную информацию о ВСФ в различных
