А.Н.Шерстнев - Математический анализ

b

( )

Za

F 0(x)dx = F (b) , F (a):

oBRATIM WNIMANIE NA TO, ^TO LEWAQ ^ASTX "PLOHO" OPREDELENA: ESLI

< x1 < : : : < xn = b |

RAZLOVENIE

,

FIGURIRU@]EE W P

DLQ

a = x0

. 2 (

KAK-NIBUDX

(WS•E RAWNO KAK!) DOOPREDELITX F 0 W \TIH TO^KAH, TO LEWAQ

^ASTX ( ) UVE STANOWITSQ KORREKTNO OPREDEL•ENNOJ. w SILU PRIMERA 46.8

LEWAQ ^ASTX ( ) NE ZAWISIT OT PROIZWOLA W OPREDELENII F 0 W KONE^NOM

^ISLE TO^EK. pO FORMULE nX@TONA-lEJBNICA 52.1

b

n

xj

n

Z

X Z

X

a

F 0(x)dx = j=1

xj,1 F0

(x)dx = j=1[F (xj) , F (xj,1)] = F (b) , F (a):

>

b

b

b

Za f(x)g0(x) dx = f (x)g(x) a , Za f0 (x)g(x)dx:

2. [fORMULA ZAMENY PEREMENNOJ]. pUSTX f

(x) (a

x

b) NEPRERYWNA,

I '(t) (c

t d) NEPRERYWNAQ KUSO^NO-GLADKAQ, PRI^•EM '(c) = a; '(d) =

b I OPREDELENA SUPERPOZICIQ f '. tOGDA

b

d

Za

f (x) dx = Zc

f ('(t))'0 (t)dt:

w SILU 53.7 S U^ETOM•

53.6 IMEEM

b

b

b

b

Za f (x)g0 (x)dx +Za f0(x)g(x) dx =Za (f (x)g(x))0 dx =f (x)g(x) a :

sWOJSTWO 1 DOKAZANO. dLQ DOKAZATELXSTWA P. 2 OBOZNA^IM ^EREZ F

PERWO-

OBRAZNU@ DLQ FUNKCII f . pUSTX RAZLOVENIE c = t0 < t1

< : : : < tn = d

TAKOWO, ^TO ' GLADKAQ NA KAVDOM OTREZKE [tj

,

1; tj

]. tOGDA

d

F ('(t)) =

f ('(t))'0

(t) (t = tj ), I PO\TOMU PO OBOB]ENNOJ•

dt

FORMULE nX@TONA-lEJBNICA

6

Zcdf ('(t))'0(t) dt = F ('(d)) , F ('(c)) = F (b), F (a) = Zabf (x)dx:

>

3. p R I M E R. wY^ISLIM J = Z01 arcsin x dx. iSPOLXZUQ 43.2, NAHODIM

PERWOOBRAZNU@ F (x) DLQ arcsin x (0 x

1)

:

F (x) = x arcsin x +

p1 , x

2

(0 x 1). s U^ETOM•

52.1 IMEEM J = F (1) , F (0) =

, 1:

2

4. z A M E ^ A N I E. zAMETIM, ^TO WYKLADKA

1

1

1

x dx

1

Z0 arcsin x dx = x arcsin x

0 , Z0

p

= 2 , p1 , x2

=

2 , 1;

1 , x2

0

DA@]AQ TOT VE OTWET, NA DANNOM

UROWNE NA[IH ZNANIJ NEPRAWOMERNA

,

TAK KAK FUNKCIQ arcsin x (0 x

1) NE QWLQETSQ NEPRERYWNOJ KUSO^NO-

GLADKOJ, I ISPOLXZOWANIE FORMULY P. 1 NEZAKONNO. dEJSTWITELXNO, INTEG-

1

x dx

RAL Z0

p

1 , x2

ZAWEDOMO NE SU]ESTWUET KAK INTEGRAL rIMANA. pOZDNEE

(x129) MY PRIDADIM SMYSL PODOBNYM WYKLADKAM.

1

xn

5. u P R A V N E N I E. nAJTI lim

Z0

1 + x

dx.

n

MOJ dARBU FUNKCII

f , OTWE^A@]EJ RAZLOVENI@ , NAZYWAETSQ SUMMA

n

n

SOOTWETSTWENNO

S ( ) = j=1 mj (xj ,xj,1 )),

GDE

S ( ) = j=1 Mj (xj ,xj,1 ) (

Mj

=

P

=

inf

P

sup f(x); mj

f (x). oTMETIM OSNOWNOE SWOJSTWO SUMM

[xj,1;xj]

[xj,1;xj]

dARBU.

3. pUSTX ; 0 | PROIZWOLXNYE RAZLOVENIQ OTREZKA [a; b]. tOGDA

S ( )

S ( 0).

pUSTX (a = x0 < x1 < : : : < xn = b) I | RAZLOVENIE, POLU^ENNOE

e

IZ

DOBAWLENIEM ODNOGO UZLA

y.

pUSTX DLQ OPREDELENNOSTI

x0 < y < x1.

•

tOGDA

S

( ) =

[ inf

f(x)](y

,

x0) + [ inf

f (x)](x1

,

y)

e +

[x0;y]

[y;x1

]

n

P

mj (xj

xj

1) [ inf

f (x)](x1

x0)

, , [x0;x1]

,

j=2

n

, xj,1) = S ( ):

+

j=2 mj (xj

WELI^INY D (f ) = inf S ( ); D

(f ) = supS

( ). oNI NAZYWA@TSQ SOOT-

b

1. oGRANI^ENNAQ FUNKCIQ f(x) (a

x

b) INTEGRIRUEMA PO rIMANU

(I = Za f(x) dx) TTOGDA

D (f ) = D (f )(= ).

nEOBHODIMOSTX. pUSTX f INTEGRIRUEMA. w SILU 46.5

8" > 09 (a = x0 < x1 < : : : < xs = b)8 j 2

[xsj,1; xj ] (j = 1; s)

,

j

j j=1

,

xj,1)

(

P

f

( j )(xj

< ").

sLEDOWATELXNO, DLQ L@BYH j 2 [xj,1; xj ] (j = 1; s)

s

, " <

X

f ( j )(xj

, xj,1) < + ":

j=1

dOSTATO^NOSTX. pUSTX D

(f ) = D (f ) = . dLQ PROIZWOLXNOGO

" > 0 (W SILU OPREDELENIQ 55.4 I SWOJSTWA 55.3) NAJDETSQ• RAZLOVENIE

~

(a = x0 < x1 < : : : < xs = b) TAKOE, ^TO

s

"

e

e

X

(Mj , mj)(xj , xj,1) <

2 :

S ( ) , S ( ) =

j=1

sLEDUET LI[X UBEDITXSQ, ^TO DLQ L@BOGO RAZLOVENIQ (a = y0 < y1 <

: : : < yN = b) DOSTATO^NO MALOGO DIAMETRA, MY BUDEM IMETX jS , j < ",

GDE S | INTEGRALXNAQ SUMMA rIMANA FUNKCII f . pUSTX M = sup

f(x)

j

I d( ) <

"

. mY IMEEM

x2[a;b] j

4Ms

S

,

= N f ( i )(yi

,

yi,1)

,

i=1

= P0f( i)(yi

yi

1) +

00f ( i )(yi

yi

1 ) ;

i

,

,

i

,

,

,

P

P

GDE SUMMA

P

0 PO TEM i, DLQ KOTORYH OTREZKI [yi

,

1; yi] SODERVAT UZLY xj

00

RAZLOVENIQ , A

| SUMMA PO OSTALXNYM i. nE OGRANI^IWAQ OB]NOSTI,

BUDEM S^ITATX

,

^TO

tOGDA TAK KAK KAVDYJ UZEL

xj

e

P

f(x) 0 (a x b).

(

MOVET PRINADLEVATX NE BOLEE ^EM DWUM OTREZKAM [yi

,

1; yi ])

Pi

,

,

Pi

,

,"

1 i N

,

,

Pi

0f ( i )(yi

yi

1)

M

0(yi

yi

1)

M max (yi

yi

1 )

01

2Msd( ) <

:

2

dLQ INDEKSOW i W SUMME

P

00

OTREZKI [yi

,

1; yi] CELIKOM LEVAT W PODHODQ]IH

i

OTREZKAH RAZLOVENIQ ; OBOZNA^AQ j

= fi : [yi,1; yi] [xj,1; xj ]g, IMEEM

00f ( i)(yi

, yi,1 )e =

s

i

j=1 i j f ( i )(yi , yi,1)

P

P P

s

2

s

j=1 Mj i j

(yi , yi,1) j

=1

Mj (xj , xj,1)

P

P

P

=

S

( ):

2

iTAK,

e

S

=

P

0 +

P

00

"

+ S ( )

" + S ( )

S

( ) < ":

,

,

2

e

,

2

e

,

e

, > ,"

aNALOGI^NO, PRI DOSTATO^NO MALYH DIAMETRAH RAZLOVENIQ S

I UTWERVDENIE DOKAZANO.

>

2. s L E D S T W I E. wSQKAQ NEPRERYWNAQ FUNKCIQ f NA OTREZKE [a; b]

INTEGRIRUEMA PO rIMANU.

"

pUSTX " > 0 PROIZWOLXNO. tAK KAK f RAWNOMERNO NEPRERYWNA (SM. 24.7),

SU]ESTWUET > 0 TAKOE, ^TO

jx

, yj

< WLE^ET•

jf (x) , f (y)j

<

.

b , a

pUSTX (a = x0 < x1 < : : : < xs

= b) | RAZLOVENIE [a; b] TAKOE, ^TO

d( ) < ". w SILU 24.2(B)

NAJDUTSQ j ; j

[xj,1; xj ] TAKIE, ^TO f ( j ) =

Mj =

sup

2 pO\TOMU

f (x); f ( j ) = mj = [xjinf,1;xj] f(x).

[xj,1;xj]

s

"

s

S ( ) , S ( ) =

X

X

[f ( j ) , f( j )](xj , xj,1 ) < b

,

a

(xj , xj,1);

j=1

j=1

(1)

J = Zab f (x) dx

WOZXMEM RAZLOVENIE

= (a = x0 < x1 < : : : < xn = b)

S RAWNOOTSTO

-

•

Q]IMI UZLAMI: xj = a +

b ,n a

j (0 j n) I WYBEREM PROMEVUTO^NYE

1

1 j n.

TO^KI W SEREDINAH POLU^ENNYH OTREZKOW: j

= 2(xj,1

+ xj);

tOGDA

Sn = b , a

n

X

(2)

f (1 (xj

,

1

+ xj ))

n

j=1

2

(3)

Tn =

b , a

n 1

(f (xj

,

1) + f(xj )):

n

j=1 2

X

tAK KAK SUMMY

b ,n a

n

f (xj,1);

b ,n a

n

f (xj ) QWLQ@TSQ INTEGRALXNYMI

j=1

j=1

P

P

1

,Z1

f (x) dx = f (,1) + f(0) + f (1)

(4)

IMELO MESTO DLQ FUNKCIJ f(x) = 1; f (x) = x; f (x) = x2. iZ SISTEMY

>

+ +

= 2

8 ,

+

= 0

<

+

= 2=3

1

>4

NAHODIM = = 3

; =:3

: s \TIMI ZNA^ENIQMI PARAMETROW FORMULA

(4) AWTOMATI^ESKI WERNA DLQ f (x) = x3

1

x3 dx = , + .

, TAK KAK 0 = ,R1

tAKIM OBRAZOM, FORMULA

1

1

,Z1

f(x)dx = 3[f(,1) + 4f (0) + f(1)]

(5)

b

b , a

[f (a) + 4f(b + a ) + f (b)]

f (x) dx =

Za

6

2

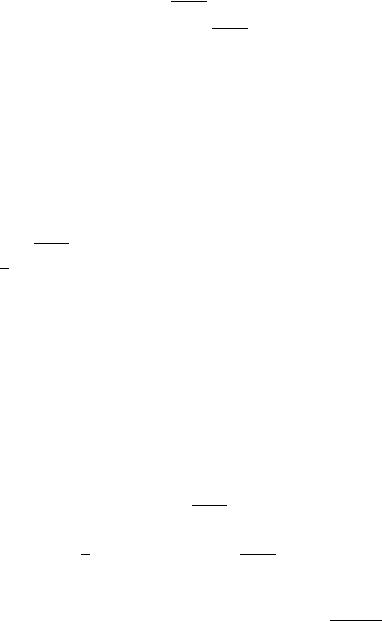
(ZDESX f | POLINOM 3-J STEPENI). dLQ POLU^ENIQ PRIBLIVENNOJ•

FORMULY

WY^ISLENIQ INTEGRALA (1)

PODELIM OTREZOK [a; b] NA 2n RAWNYH PODOTREZ-

KOW S KONCAMI xj = a +

b , a

j I NA KAVDOM OTREZKE [x2j

,

2; x2j ] INTEGRAL

x2j

2n

b , a

f (x)dx ZAMENIM SUMMOJ

[f(x2j

,

2) + 4f(x2j

,

1) +f(x2j )]. sUMMI-

Zx2j,2

6n

RUQ PO j, POLU^IM

n = n

b , a[f (x2j

2) + 4f

(x2j 1 ) + f (x2j )]:

X

6n

,

,

j=1

b

1

b

Za f (x) dx , (b , a)f ( 1)

Za f00

2

(6) R1

=

=

2

(c)(x , 1 ) dx

M

b

2

M

b

a

3

,

3

2

2 Za

(x

1) dx =

:

,

w SLU^AE PROIZWOLXNOGO n ZAMETIM, ^TO

b

n

n

xj

n

Zn

xj

P

P Z

P

, b

Rn = j a f (x) dx

,n a j=1 f ( j )j = jj=1

xj,1 f (x)dx , b ,n a j=1 f ( j )j

Rn

M

n

b , a

!

3 =

M

(b , a)3

:

3

24

n2

2n