
ЛЕКЦИЯ 8_9,15.11.11_
.pdf
ЛЕКЦИЯ 8 (8.11.11)
Алгебраические критерии устойчивости линейных систем: Стодола, Гурвица.
Частотные критерии устойчивости: метод D-разбиения, критерий Михайлова.
В инженерной практике не всегда удобно проверять устойчивость ли-
нейной системы по корням характеристического уравнения. Это связано в первую очередь с необходимостью использования ЦВМ, поскольку для ал-
гебраических уравнений выше 3-его порядка требуется использование чис-
ленных методов. Кроме того, часто требуется определять область устойчиво-
сти системы по параметрам. При этом вычисление корней характеристиче-
ского уравнения для множества значений параметров является нерациональ-
ным. В связи с этим возникает задача определения устойчивости системы без вычисления корней, т.е. определения условий при которых корни характери-
стического уравнения левые. Методы, решающие указанную задачу, называ-
ются критериями устойчивости. В зависимости от метода решения задачи критерии устойчивости делятся на алгебраические и частотные. Алгебраи-
ческие позволяют судить об устойчивости системы по коэффициентам ха-
рактеристического уравнения системы, а частотные – по виду соответст-
вующих частотных характеристик.
1. Алгебраические критерии устойчивости.
Пусть задано характеристическое уравнение линейной системы
D(p) | pE |
A| a |
pn a pn 1 a |
n |
0, |
a 1. |
(1) |
||||
n |
0 |
1 |
|
0 |
|
|
|
|
|
|
1.1. Критерий Стодола. Для устойчивости системы с характеристиче- |
||||||||||
ским уравнением (1) необходимо, чтобы коэффициенты ai |
0, i |
|
. |
|
|
|||||
0,n |
||||||||||
Доказательство. В соответствии с теоремой Безу уравнение (1) можно |
||||||||||
представить в виде произведения множителей, содержащих корни pi , |
i |
|
: |
|||||||
1,n |
||||||||||
D(p) a0(p p1)(p p2) (p pn) 0. |
(2) |
|||||||||
Пусть все корни левые, причем для вещественных корней коэффициен-
ты pi 0, а для комплексно-сопряженных корней pi i j i , pi 1 pi i j i множители
1
(p pi)(p pi 1) p2 (pi pi 1)p pi pi 1 p2 2 i p i2 i2
имеют полиномы 2-го порядка с положительными коэффициентами, по-
скольку i 0. Тем самым, если раскрыть полином (2) с положительными коэффициентами и привести к виду уравнения (1), то его коэффициенты так-
же будут положительными. Отсюда следует критерий Стодола.
Очевидно, что возможны случаи, когда некоторые коэффициенты урав-
нения (2) отрицательные, а коэффициенты уравнения (1) положительные, т.е.
критерий Стодола является только необходимым. Однако, если в уравнении
(1) хотя бы один коэффициент ai 0, то система неустойчива. Это условие является достаточным для неустойчивости системы.
1.2. Критерий Гурвица. Для устойчивости системы с характеристиче-
ским уравнением (1) необходимо и достаточно, чтобы матрица Гурвица
a1 |
a3 |
a5 |
|
0 |
|
|
|
|
a2 |
a4 |
|
0 |
|
a0 |
|
|||||
à 0 |
a1 |
a3 |
0 |
|||
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
0 |
|
|
a |
|
|
|
|
|
|
n |
|
имела положительные главные диагональные миноры:
a 0, |
|
|
a1 |
a3 |
0, …, |
|
| Ã | a |
|
0. |
|
1 1 |
2 |
|
a |
a |
2 |
|
n |
n |
n 1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
Рассмотрим частные случаи:
1) при n 2 условие устойчивости определяется неравенствами
a 0, |
|
|
|
a1 |
0 |
a a 0, |
1 1 |
|
2 |
|
a |
a |
1 2 |
|
|
|
|
0 |
2 |
|
т.е. a0 1 0, a1 0, a2 0, что совпадает с условием критерия Стодола, ко-
торый в этом случае дает необходимое и достаточное условие устойчивости. 2) при n 3 условие устойчивости определяется неравенствами
a 0, |
|
|
|
a1 |
a3 |
aa |
a a 0, |
|
a |
|
0, |
1 1 |
|
2 |
|
a a |
1 2 |
0 3 |
3 |
3 |
2 |
|
|
|
|
|
|
0 |
2 |
|
|
|
|
|
|
2
из которых следует, что |
ai 0, i 1,3 и должно выполняться условие |
|||||
aa a a . |
|
|
||||
1 |
2 |
0 |
3 |
|
|
|
|
|
Таким образом, из критерия Гурвица следуют необходимые условия |
||||
устойчивости Стодола. |
|
|
||||
|
|
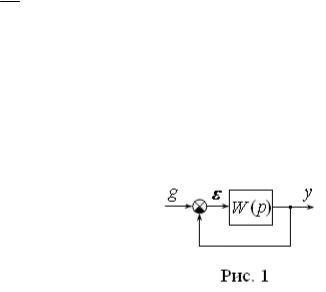
Пример 1. Пусть структурная схема САУ имеет вид рис. 1, где |
||||
|
|
|
W(p) |
|
k |
|
|
|
|
|
|
. |
|
|
|
|
|
|
||
p(T1p 1)(T2 p 1)
Требуется определить условие устойчивости замкнутой системы по коэффициенту усиления k .
Для решения задачи составим характеристическое уравнение замкну-
той системы, полагая 1 W(p) 0. Отсюда получим
D(p) p(T1p 1)(T2 p 1) k 0
или
|
|
|
|
|
D(p) a p3 |
a p2 a p a 0, |
|
||||||
|
|
|
|
|
|
|
0 |
|
1 |
2 |
|
3 |
|
где a |
TT |
0, |
a T T |
0, a |
2 |
1, |
a k 0. Тогда условие устойчиво- |
||||||
0 |
1 |
2 |
|
1 |
1 |
2 |
|
|
3 |
|
|
|
|
сти замкнутой системы определяется неравенством a1a2 a0a3 |
или с учетом |
||||||||||||
подстановки |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0 k |
T1 T2 |
. |
|
(3) |
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
T1T2 |
|
|
|
Критерий Гурвица удобно использовать для систем невысокого поряд-
ка (n 6), поскольку с ростом порядка увеличивается объем аналитических вычислений. Если требуется определить область устойчивости по одному па-
раметру, то для систем высокого порядка можно воспользоваться символь-
ными вычислениями пакета MATLAB.
Пример 2. Требуется определить область устойчивости системы
|
0 |
1 |
0 |
|
|
x |
|
0 |
0 |
1 |
|
|
x |
||||
|
|
|
1 |
|
|
|
k |
2 |
|||
по коэффициенту k с помощью символьных вычислений.
3
Для решения задачи воспользуемся следующим Script-файлом:
syms p k % символьные переменные n=3; A=[0 1 0;0 0 1;-k -1 -2];
d=poly(A,'p')% определение характеристического уравнения
%вектор коэффициентов характеристического уравнения aa=coeffs(d,p);n1=n+1;for i=1:n1; a(i)=aa(n1-i+1);end
%второй главный диагональный минор матрицы Грвица delta2=[a(2) a(4);a(1) a(3)]
vpa(det(delta2),6)% выражение минора матрицы Гурвица
В результате выполнения данной программы на печать выводятся вы-
ражение характеристического уравнения, второй главный диагональный ми-
нор матрицы Гурвица и его выражение:
d =
p^3+2*p^2+p+k
delta2 =
[ 2, k] [ 1, 1]
detG =
2.-1.*k
Таким образом, условие устойчивости по коэффициенту k определяет-
ся неравенством 0 k 2.
2. Частотные критерии устойчивости
При значении порядка системы n 6 использование критерия Гурвица связано с решением сложных неравенств. В этом случае для определения об-
ласти устойчивости более эффективным является частотный метод D –
разбиения, предложенный Ю.И. Неймарком, который в отличие от алгебраи-
ческого метода является численным методом.
2.1. Метод D-разбиения
Сущность метода D – разбиения по одному параметру заключается в
следующем. Пусть характеристическое уравнение системы имеет вид: |
|
D(p,k) d(p) k m(p) 0, |
(4) |
где k неизвестный параметр, по которому требуется определить область ус-
4

тойчивости системы. Из уравнения (4) запишем выражение для параметра k
в операторной форме:
k(p) d(p) . m(p)
При подстановке p j для значений определяется усло-
вие на комплексный параметр k( j ), при котором замкнутая система имеет
корни |
на мнимой |
оси. Построенная кривая D - разбиения |
k( j ) |
X( ) jY( ) |
при разбивает комплексную плоскость на |
области с различным содержанием устойчивых корней. При переходе из од-
ной смежной области в другую через кривую D - разбиения один веществен-
ный или пара комплексных сопряженных корней переходит через мнимую ось. Область, содержащая наибольшее число левых корней называется пре-
тендентом на устойчивую область.
Для установления правила, определяющего область претендент, рас-
смотрим пример при n 1. |
|
|
|
|
Полагая D(p,k) p k 0, |
получим |
k p |
и, |
следовательно, |
k(j ) j , X( ) 0, Y( ) . |
Тем самым |
кривая D |
- |
разбиения k( j ) |
проходит по мнимой оси и разделяет комплексную плоскость на две области.
Из характеристического уравнения следует, что система устойчива при k 0,
т.е. при X( ) 0. Если нанести штриховку на кривой D - разбиения k( j )
слева при изменении от до , то область устойчивости будет на сто-
роне штриховки. Тем самым в данной области наибольшее число устойчивых корней (один единственный корень). При переходе из правой полуплоскости
(со стороны штриховки) в левую полуплоскость один корень становится не-
устойчивым и наоборот. Данные свойства также справедливы для n 2.
В общем случае для системы n-го порядка, если суммарное число пе-
реходов корней при переходах из области с наименьшим числом в область с наибольшим числом левых корней равно n, то область претендент будет об-
ластью устойчивости.
5
Если число таких переходов меньше n, то найденную область претен-
дент необходимо проверить на устойчивость для любого фиксированного вещественного значения параметра k из данной области с помощью какого-
нибудь критерия устойчивости. Здесь можно воспользоваться, например,
критерием Гурвица с использованием численных методов вычисления глав-
ных диагональных миноров.
Построение области устойчивости по параметру k методом D - раз-
биения можно проводить в системе MATLAB с помощью функции nyquist
для операторного выражения параметра k(p).
Пример 3. Для примера 1 требуется построить кривую D-разбиения при значении параметров T1 1с, T2 0,1с.
Для решения задачи воспользуемся командой
T1=1; T2=0.1; nyquist(-tf([T1*T2 T1+T2 1 0],[1]))
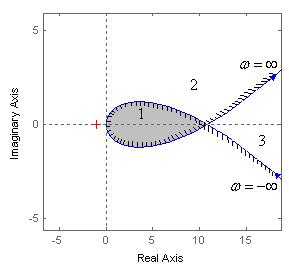
На рис. 2 представлен отредактированный график кривой D-разбиения,
разделяющей комплексную плоскость на три области. При этом область 1 яв-
ляется областью претендентом на устойчивость со значением параметра k ,
удовлетворяющего неравенству 0 k 11, что совпадает с условием устой-
чивости по критерию Гурвица (3).
Рис. 2
6
Метод D-разбиения также применяется для определения областей ус-
тойчивости по двум параметрам [5, с. 155-167].
2.2. Критерий устойчивости Михайлова
Другой частотный способ определения устойчивости линейной систе-
мы связан с построением частотной характеристики D( j ), называемой го-
дографом Михайлова, для уравнения (1) при изменении 0 .
Рассмотрим свойства годографа D( j ) с учетом выражения (2):
n |
n |
|
D( j ) | D( j )|ejargD( j ) ( j pi) |
| j pi | ejarg( j pi) , |
(5) |
i 1 |
i 1 |
|
где |
|
|
n |
|
|
| D( j )| | j pi |
|, |
(6) |
i 1 |
|
|
n |
|
|
argD(j ) arg(j pi). |
(7) |
|
i 1 |
|
|
Здесь принято обозначение arg() – аргумент от комплексного значения, рав-
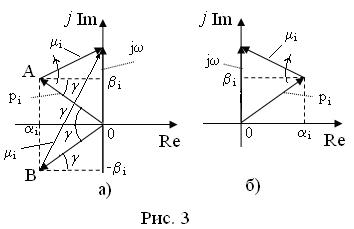
ный значению фазы. На рис. 3 для удобства комплексные значения представ-
лены в виде векторов.
Рассмотрим случай левых корней pi (рис. 3а), где i j pi . Найдем диапазон изменения (приращение) аргумента для функции i j pi при изменении 0 . Очевидно, что вектор i (т. А) повернется на угол
/2 .
7

Для комплексно-сопряженного значения pi i j i вектор i (т. В)
повернется на угол /2 . Тогда приращение аргумента для функции
(j pi)( j pi) будет равно сумме приращений аргумента для каждого
множителя:
arg[( j pi)( j pi)] /2 /2 2 /2.
0
Для вещественного корня ( i 0, 0) получим приращение аргу-
мента
arg[ j pi] /2.
0
Рассмотрим случай правых корней pi (рис. 3б). Очевидно, что прира-
щения аргумента для правых корней будет отличаться только знаком.
Таким образом, левые корни характеристического уравнения (1) дают
положительное, а правые отрицательное приращение аргумента.
На основе проведенного анализа с учетом формулы (7) можно сформу-
лировать следующее свойство.
Свойство. Если характеристическое уравнение (1) имеет m правых и n m левых корней, то приращение аргумента для годографа Михайлова
(5) будет равно:
arg D( j ) (n m) / 2 m / 2 (n 2m) / 2. |
(8) |
0 |
|
|
|
Отсюда следует, что если построить годограф Михайлова D( j ) |
и оп- |
ределить из графика его приращение аргумента, равное k /2, то из равен-
ства k /2 (n 2m) /2 найдем количество правых корней по формуле
m (n k)/2. |
(9) |
Если приращение аргумента arg D( j ) n /2, то m 0 и, следова-
0
тельно, система устойчива. При этом годограф Михайлова вращается строго против часовой стрелки.
При определении устойчивости системы по приращению аргумента го-
8

дографа D( j ) необходимо исключать случаи расположения корней на мнимой оси (на границе устойчивости). В этих случаях годограф Михайлова имеет характерный вид.
1. Если имеется пара чисто мнимых корней p1,2 j i , то согласно формуле (6) при i значение | D( j )| 0, т.е. годограф Михайлова про-
ходит через начало координат.
2. Если имеется нулевой вещественный корень p1 0, то при 0
значение | D( j )| 0, т.е. годограф Михайлова начинается из начала коор-
динат.
Отметим, что для устойчивости системы в силу критерия Стодола все коэффициенты характеристического уравнения должны быть положитель-
ными, т.е. в уравнении (1) значение an 0 и годограф Михайлова при 0
должен начинаться на вещественной положительной полуоси.
С учетом указанных свойств теперь можно дать общую геометриче-
скую интерпретацию частотного критерия устойчивости Михайлова:
Для устойчивости системы с характеристическим уравнением (1) не-
обходимо и достаточно, чтобы годограф Михайлова начинался на вещест-
венной положительной полуоси, строго вращался против часовой стрелки,
последовательно обходя n квадрантов (не проходя через начало координат),
и уходил в бесконечность в n-ом квадранте, где n– порядок характеристи-
ческого уравнения.
Для построения годографа Михайлова необходимо:
1)представить D( j ) X( ) jY( );
2)найти точки пересечения с вещественной осью, полагая Y( ) 0 и
определяя соответствующие положительные значения 1, 2 , … в порядке возрастания;
9
3) найти точки пересечения с мнимой осью, полагая X( ) 0 и опре-
деляя соответствующие положительные значения 1, 2 , … в порядке воз-
растания;
4) определить квадрант, в котором годограф уходит в бесконечность по
значениям X( ), Y( ).
По полученным точкам пересечения с осями координат в порядке воз-
растания частоты можно построить годограф Михайлова.
Из геометрической интерпретацию критерия Михайлова следует, что для устойчивости системы необходимо и достаточно, чтобы пересечение
осей |
X( ), |
Y( ) |
осуществлялось |
в |
последовательности |
1 1 |
2 2 ... |
и годограф Михайлова уходил в бесконечность в n-ом |
|||
квадранте.
Нарушение хотя бы одного свойства в формулировках критерия ус-
тойчивости свидетельствует о неустойчивости системы.
Построение годографа Михайлова можно проводить в системе MATLAB с помощью функции nyquist для полинома D(p).
Пример 4. Для примера 3 построить годографы Михайлова при значе-
ниях k 0, k 5, k 11, k 15 и сделать выводы об устойчивости системы.
Для решения задачи воспользуемся Script-файлом:
T1=1;T2=0.1;
k=0;[u,v,w]=nyquist((tf([T1*T2 T1+T2 1 k],[1])),{1e-8,10}); plot(squeeze(u),squeeze(v));hold on k=5;[u,v,w]=nyquist((tf([T1*T2 T1+T2 1 k],[1])),{1e-8,10}); plot(squeeze(u),squeeze(v)); k=11;[u,v,w]=nyquist((tf([T1*T2 T1+T2 1 k],[1])),{1e-8,10}); plot(squeeze(u),squeeze(v)); k=15;[u,v,w]=nyquist((tf([T1*T2 T1+T2 1 k],[1])),{1e-8,10}); plot(squeeze(u),squeeze(v));grid
На рис. 4 представлены отредактированные графики годографов Ми-
хайлова: годограф 1 (k 0) начинается из начала координат и соответствует апериодической границе устойчивости системы; годограф 2 (k 5) последо-
вательно обходит три квадранта, что свидетельствует об устойчивости сис-
темы; годограф 3 (k 11) проходит через начало координат, тем самым сис-
10
