ЛЕКЦИЯ 9_16,22.11.11_

ЛЕКЦИЯ 9 _16, 22.11.11_

Частотный критерий устойчивости Найквиста. Логарифмический аналог критерия Найквиста. Запасы устойчивости. Устойчивость систем с запаздыванием. Интервальный критерий Найквиста.

1. Частотный критерий устойчивости Найквиста.

В отличие от критерия Михайлова частотный критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по АФЧХ

разомкнутой системы, которая может быть построена аналитически или экспериментально.

Рассмотрим структурную схему замкнутой системы, представленную на рис. 1, которую можно представить в виде рис. 2. Тем самым, замкнутую одномерную систему всегда можно представить в виде рис. 3, где передаточ-

ная функция разомкнутой системы W(p) W1(p)W2(p) охвачена отрицатель-

ной единичной обратной связью. Далее будем рассматривать такую систему с передаточной функцией W(p) m(p)/d(p), у которой порядок числителя m не превышает порядка знаменателя n, что соответствует условию физиче-

ской реализуемости.

Для структурной схемы рис. 3 выражение изображения выхода имеет

вид

Y(p) W(p) G(p), 1 W(p)

из которого следует уравнение свободного движения системы при G(p) 0:

1

1 W(p) Y(p) 0.

Характеристическое уравнение замкнутой системы определяется из

уравнения

1 W(p) 0.

где d(p) 0 – характеристическое уравнение разомкнутой системы n-го

порядка, D(p) d(p) m(p) 0 – характеристическое уравнение замкнутой системы n-го порядка.

1. Рассмотрим случай, когда характеристическое уравнение разомкну-

(n 2l) /2 (n 2m) /2 2 (m l)/2.

Для устойчивости замкнутой системы необходимо и достаточно, чтобы l 0 и тем самым, годограф F( j ) при изменении 0 должен охваты-

вать начало координат в положительном направлении m/2 раз.

Данное условие устойчивости можно переформулировать для АФЧХ разомкнутой системы W( j ). На рис. 4 представлен годограф F( j ), век-

тор

2

ближенными множителями p , p2 p *2 , где 0 – сколь угодно ма-

лое значение. Иначе говоря, корни, расположенные на мнимой оси сдвинули в левую полуплоскость на бесконечно малое значение и тем самым пришли к предыдущему случаю. При этом АФЧХ приближенной передаточной функ-

ции W( j ) начинается на вещественной оси, изменение фазы происходит непрерывно с бесконечно большим значением модуля |W( j )| в окрестности точек 0 и *. К построенной АФЧХ W( j ) можно применить крите-

рий Найквиста, полагая 0.

Таким образом, для использования критерия Найквиста в рассматри-

ваемом случае необходимо построить АФЧХ W( j ) и места разрывов ее ха-

рактеристики по часовой стрелке (отрицательное приращение фазы) допол-

нить дугами бесконечно большого радиуса.

На рис. 6 приведена АФЧХ передаточной функции W(p), содержащей два нулевых полюса (два интегрирующих звена). Очевидно, что АФЧХ

W( j ), дополненная дугой бесконечно большого радиуса R , один раз охватывает точку ( 1, j0) в отрицательном направлении, т.е. 1 m/2. Сле-

довательно, замкнутая система неустойчива при любом m.

На рис. 7 приведена АФЧХ передаточной функции W(p), содержащей пару чисто мнимых полюсов (консервативное звено). Очевидно, что АФЧХ

W( j ), дополненная дугой бесконечно большого радиуса R , один раз охватывает точку ( 1, j0) в отрицательном направлении, т.е. 1 m/2. Сле-

довательно, замкнутая система неустойчива при любом m.

4

На рис. 6, рис. 7 АФЧХ имеет один отрицательный переход.

На рис. 8 АФЧХ разомкнутой системы имеет отрицательный и поло-

жительный переход, сумма которых равна нулю. Тем самым условие устой-

чивости замкнутой системы 0 m/2 выполняется при m 0.

Если АФЧХ разомкнутой системы не имеет переходов вещественной полуоси ( , 1), то сумма переходов равна нулю.

6

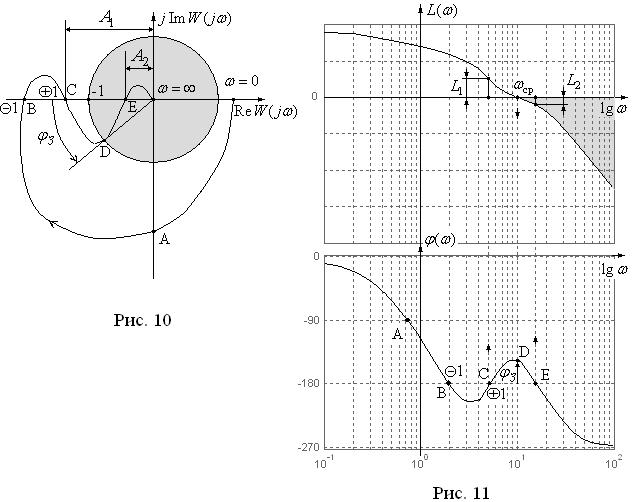
2. Логарифмический аналог критерия Найквиста.

Установим связь переходов для АФЧХ с переходами для ЛАХ и ЛФХ.

Для этого рассмотрим рис. 10 и рис. 11, на которых отмечены характерные

точки. На рис. 10 и рис. 11 отрицательному переходу соответствует убыва-

ние, а положительному возрастание значения ( ).

Если АФЧХ разомкнутой системы, представленной на рис. 10, зер-

кально отобразить относительно вещественной оси, то ЛФХ на рис. 11 также зеркально отобразиться относительно оси частот, а ЛАХ при этом останется прежней. Для такой разомкнутой системы условие устойчивости по крите-

рию Найквиста не изменится. В этом случае ЛФХ будет пересекать ось .

Таким образом, переходам АФЧХ вещественной полуоси ( , 1) на рис.10 соответствует область положительных значений L( ), для которых

|W( j )| 1, и значение ( ) ; 3 ; 5 ; .

7

Область, в которой |W( j )| 1 или L( ) 20lg|W(j )| 0 (на рисун-

ках закрашена) не влияет на устойчивость замкнутой системы. Значение час-

тоты ср , при которой |W( j ср)| 1 или L( ср) 1 называется частотой сре-

за.

В общем случае может существовать несколько частот среза, т.е. не-

сколько участков положительных значений ЛАХ.

С помощью переходов критерий Найквиста можно сформулировать

так:

Для устойчивости замкнутой системы с единичной отрицательной об-

ратной связью необходимо и достаточно, чтобы в области частот, где

L( ) 0, сумма переходов с учетом знаков ЛФХ разомкнутой системы че-

рез линии ( ) ; 3 ; 5 ; равнялась m/2, где m – число правых корней характеристического уравнения разомкнутой системы.

3. Запасы устойчивости.

Запасы устойчивости – это величины, которые количественно характе-

ризуют удаление устойчивой системы от границы ее устойчивости. На ком-

плексной плоскости для левых корней характеристического уравнения запа-

сом устойчивости можно считать наименьшее расстояние корня до мнимой оси. Запасом устойчивости замкнутой системы можно считать удаление АФЧХ разомкнутой системы от точки ( 1, j0).

Действительно, если АФЧХ разомкнутой системы W( j ) при

0 0 проходит через точку ( 1, j0), то замкнутая система имеет пару чисто мнимых корней. Это следует из условия W(j 0) 1, которому соот-

ветствует уравнение

1 W( j 0) D( j 0) 0, d( j 0)

где характеристическое уравнение замкнутой системы D( j 0) 0 должно иметь пару чисто мнимых корней p1,2 j 0.

8

Если АФЧХ разомкнутой системы W( j ) при 0 начинается из точки ( 1, j0), то замкнутая система имеет нулевой корень.

Таким образом, при выполнении устойчивости замкнутой системы АФЧХ разомкнутой системы не должна проходить вблизи точки ( 1, j0).

Удаление от этой точки характеризуется запасами по амплитуде A1, A2 (рис. 10) или L1 20lg A1, L2 |20lgA2 | (рис. 11), запасами по фазе З , равные ближайшим углам между вещественной полуосью ( ,0] и лучам, проходя-

щим через начало координат и соответствующую точку W( j ср).

9

4. Устойчивость систем с запаздыванием.

Система с запаздыванием имеет передаточную функцию разомкнутой

системы, содержащую звено чистого запаздывания e p :

не является алгебраическим полиномом, то критерий Гурвица здесь не при-

меним.

Кроме того, функция e p 1 p p2 2 /2! ( 1)N N /N! яв-

ляется бесконечным рядом степени p, т.е. уравнение (4) имеет бесчисленное

множество корней. Поэтому критерий Михайлова также не применим.

Однако ответить на вопрос об устойчивости корней характеристиче-

ского уравнения (4) можно с помощью критерия Найквиста. Для этого вместо передаточной функции (3) будем использовать приближенную передаточную

функцию

где – сколь угодно малое, N сколь угодно большое целое число.

Очевидно, что при 0 передаточная функция W(p) W(p). Также отметим, что при 0 согласно критерию Найквиста устойчивость замкну-

той системы не зависит от сколь угодно малой постоянной времени .

Передаточной функции (5) соответствует функция

F(p) 1 W(p) d(p)( p 1)N m(p)e p , d(p)( p 1)N

у которой при N порядок полиномов числителя и знаменателя можно считать одинаковыми. Тогда согласно критерию Найквиста для устойчивости замкнутой системы необходимо и достаточно, чтобы приращение аргумента

10