
Lectures part2
.pdf
- 151 -
принимают родственную ей гипотезу Кирхгоффа-Лява: материальные точки оболочки, до деформации находившиеся на нормали к срединной поверхности оболочки (срединной плоскости пластины), после деформации остаются на нормали к деформированной срединной поверхности. Введение этой гипотезы также означает отказ от установления точных законов распределения напряже- ний и других величин по толщине оболочки. Вместо напряжений уравнения равновесия записываются относительно внутренних силовых факторов (погон- ных внутренних сил и моментов в оболочке). Определения для этих величин вполне аналогичны определениям внутренних силовых факторов в брусе, и для тонких оболочек они могут быть приняты в следующей форме:
|
h 2 |
h 2 |
h 2 |
Nx = òsxdz , Ny = òsydz , Nxy = òtxydz , |
|||
|
−h 2 |
−h 2 |
−h 2 |
|
h 2 |
h 2 |
|
Qx = |
òtxzdz , Qy = |
òtyzdz , |
(30.1) |
−h 2 |
−h 2 |
|
|
|
h 2 |
h 2 |
h 2 |
M x = |
òsx zdz , M y = òsy zdz , |
M xy = òtxy zdz , |
|
|
−h 2 |
−h 2 |
−h 2 |
где x, y – криволинейные координаты на срединной поверхности обо- лочки (рис. 30.1); z – прямолинейная координата, перпендикулярная коорди- натным линиям x = const и y = const и направленная вдоль нормали к оболоч- ке; Nx , N y , Nxy – погонные силы в плоскости, касательной к срединной по-
верхности оболочки, так называемые мембранные усилия; Qx , Qy – погонные перерезывающие силы; M x , M y , M xy – погонные изгибающие и крутящий мо-
мент в оболочке. Все силовые факторы названы погонными, так как представ- ляют собой, как нетрудно видеть из их определений, силы и моменты, прихо- дящиеся на единицу длины координатной линии. На рисунке показаны их по- ложительные направления.
Напряжения по погонным силам и моментам также вычисляются анало- гично задачам для брусьев (сравни с напряжениями в стержне прямоугольного сечения):
sx = |
N |
x |
+ |
12M |
x |
z , sy = |
Ny |
+ |
12M y |
z , txy = |
Nxy |
+ |
12M xy |
z , |
(30.2) |
||
|
|
h3 |
|
h |
|
h3 |
h |
|
h3 |
||||||||
|
h |
|
|
|
|
|
|
|
|
|
|||||||
для поперечных касательных напряжений (в направлении оси z) можно полу- чить формулы, аналогичные формуле Журавского для прямоугольного сечения:
|
|
|
6Q |
æ h2 |
|
2 |
ö |
|
|
|
|
6Qy æ h2 |
|
2 |
ö |
|
|
|||||
t |
xz |
= |
|
x |
ç |
|
- z |
|
÷ |
, |
t |
yz |
= |
|
|
ç |
|
- z |
|
÷ |
, |
(30.3) |
|
3 |
|
|
|
3 |
|
|
|||||||||||||||
|
|
h |
ç |
4 |
|
|
÷ |
|
|
|
h |
ç |
4 |
|
|
÷ |
|
|
||||
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
è |
|
|
ø |
|
|
||||
напряжением же σz , как и в брусьях, обычно пренебрегают.

- 152 -
Однако погонные силовые факторы, входящие в эти формулы, представ- ляют собой функции двух независимых переменных в статических задачах, на-  z пример, Nx (x, y), N y (x, y), ... . Для пла-
z пример, Nx (x, y), N y (x, y), ... . Для пла-
|
|
|
Qy |
|
Qx |
|
|
|
|
|
|
|
M y |
y |
|
M x |
Ny |
||
|
Nxy |
|||
x |
N |
xy |
M xy |
|
Nx |
M xy |
|
|
|
P/2 |
Рис. 30.1 |
P/2 |
||
|
|
|
||
A |
|
|
|
B |
a |
P |
|
|
a |
Эпюра Qy (x) |
|
|
|
|
A  B
B  P/2
P/2
Эпюра M z (x) |
M z max = Pa 2 |
A |
B |
Рис. 30.2 |
|
P a
a 
A












 B
B
Рис. 30.3
стин и оболочек их можно найти обычно только из системы дифференциальных уравнений в частных производных, в от- личие от стержней, рассмотренных в данном курсе. Так что задача отыскания
этих величин представляет собой задачу высокой математической сложности.
Ещё одним обстоятельством, ус-
ложняющим расчётные соотношения для оболочек, является необходимость использования криволинейных коорди- нат в срединной поверхности оболочки,
что обусловлено введением гипотез в перпендикулярном к этим координатам направлении, в котором размеры оболо- чек малы. Аналогичная трудность воз- никает и при расчете кривых брусьев.
Простейшие криволинейные системы координат, сферическая и цилиндриче- ская, изучаются в обычных курсах ма- тематики технических вузов, однако для брусьев и оболочек произвольных очер- таний приходится использовать произ- вольные криволинейные координаты, а они обычно не изучаются, поэтому ос- танавливаться на построении общих со- отношений для оболочек здесь невоз- можно, и будут рассмотрены только от- дельные частные задачи.
|
|
|
Расчёт тонких осесимметрич- |
|
|
|
ных оболочек вращения по |
|
основная |
|
безмоментной теории |
|
|
Напряжённо-деформированное со- |
|
A |
система |
B |
|
|
|
|
стояние (НДС) кривых стержней и оболо- |
|
Рис. 30.4 |
|
чек сильно отличается от НДС стержней и |
|
|
|
- 153 -
пластин, хотя математические модели их схожи. В искривлённых элементах ос- новную роль начинают играть мембранные усилия, а большие изгибающие мо- менты возникают только в локальных зонах около опор, в местах резкого измене- ния формы (перелом поверхности, скачкообразное изменение её толщины), в мес-
тах приложения сосредоточенных и резко изменяющихся нагрузок. |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
качестве |
примера |
рассмотрим |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
балку на двух шарнирно неподвижных |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
опорах (рис. 30.2). От изображённой на |
|||||||
|
|
H |
эквивалентная |
|
рисунке силы при малых перемещениях и |
|||||||||||||||||||
|
|
B |
деформациях в ней возникают только пе- |
|||||||||||||||||||||
A |
|
|
|
|
|
|
система |
ререзывающие |
силы |
и изгибающие |
мо- |
|||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
Рис. 30.5 |
|
менты, эпюры которых также изображены |
||||||||||||||
|
|
|
|
|
|
|
|
|
на рисунке. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По-другому распределяются внут- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
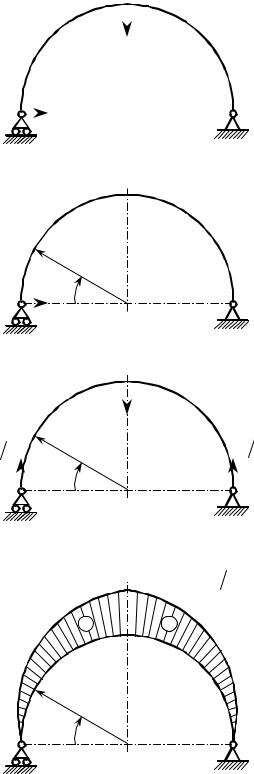
ренние силовые факторы в двухшарнир- |
|||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
ной круговой |
арке, |
изображённой |
на |
||||||||
|
|
|
ϕ |
|
|
|
|
|
|
|
|
(рис. 30.3). При их определении |
прихо- |
|||||||||||
A |
|
|
|
|
|
|
|
|
B |
дится учитывать, что арка один раз стати- |
||||||||||||||
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
=1 |
|
|
|
|
|
|
|
|
|
|
чески неопределима. В качестве основной |
||||||||||||
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
Рис. 30.6 |
|
системы можно выбрать арку на статиче- |
||||||||||||||
|
|
|
|
|
|
|
|
|
ски определимых опорах, убрав дополни- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
тельную горизонтальную связь, например, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в опоре А (рис. 30.4). Эквивалентной сис- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
P 2 |
|
|
a |
|
|
|
|
|
|
|
P 2 |
темой будет арка на рис. 30.5. Сила распо- |
||||||||||||
|
ϕ |
|
|
|
|
|
|
|
ра Н, представляющая собой горизонталь- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ную реакцию в опоре, будет неизвестной в |
|||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
каноническом уравнении |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Рис. 30.7 |
|
δ11H + 1P = 0 |
|
|
(30.4) |
|||||||||||
Эпюра M P (ϕ) |
|
|
|
|
|
|
|
|
Приложив к основной системе еди- |
|||||||||||||||
|
|
M max = Pa 2 |
ничную |
силу |
~ |
|
(рис. 30.6), |
найдем |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
H =1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соотношение для эпюры от единичного |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нагружения M (ϕ) . В качестве координа- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ты для этой эпюры используем угол ϕ . |
|||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
Из уравнения равновесия моментов, дей- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ствующих на отсечённую часть, запишем |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
ϕ |
|
|
|
|
|
|
|
|
~ |
|
~ |
|
|
|
(30.5) |
||||||
A |
|
|
|
|
|
|
|
|
B |
M (ϕ) = −Hasin ϕ = −asin ϕ . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С помощью этой же координаты |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Рис. 30.8 |
|
получим |
эпюру |
M P (ϕ) от |
нагрузки |
ис- |
||||||||||
|
|
|
|
|
|
|
|
|
ходной конструкции, приложенной к ос- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

- 154 -
новной системе (рис. 30.7). В силу симметрии задачи вертикальные опорные реакции равны 0,5P . Снова из равновесия моментов получаем
Эпюра NP (ϕ) |
|
|
|
|
|
|
|
M P (ϕ) = 0,5Pa(1− cosϕ) . |
(30.6) |
||||||||
|
|
|
|
|
|
|
Из уравнений равновесия в проекциях на |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
координатные направления в точке Х |
|||
|
|
a |
|
|
|
|
|
|
|
найдём и силы в поперечных сечениях |
|||||||
|
|
|
|
|
|
|
|
|
арки: |
|
|
|
|||||
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
B |
NP (ϕ) = −0,5Pcosϕ , |
|
(30.7) |
||||||
A |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
Qp |
(ϕ) = 0,5Psin ϕ . |
|
(30.8) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Nmax = −0,5P |
|
|
|
Полученные эпюры (рис. 30.8 – |
|||||||
|
|
|
|
|
|
Рис. 30.9 |
|
|
|
30.10) дают распределение |
внутренних |
||||||
|
|
|
|
|
|
|
|
|
силовых факторов в поперечных сечени- |
||||||||
Эпюра QP (ϕ) |
|
|
Q |
= 0,5P |
|||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
max |
|
|
|
ях арки без дополнительной горизон- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тальной связи, распора. Максимальные |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
моменты в такой арке остаются теми же, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
что и в балке на рис. 30.2. |
|
|
|
|
|
Q |
= −0,5P |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Записав соответствующие интегра- |
|||||||||||
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
ϕ |
|
|
|
|
|
|
|
лы Мора, найдём коэффициенты канони- |
|||||||
A |
|
|
|
|
|
|
B |
ческого |
уравнения. При |
этом |
надо |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
учесть, что интегралы Мора берутся по |
|||
|
|
|
|
Рис. 30.10 |
|
|
|
длине стержня, в данном случае по длине |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дуги оси арки s, и чтобы перейти к ин- |
|||
тегрированию по углу ϕ, следует заменить переменную. Кроме того, ввиду симметрии задачи, получаются два одинаковых интеграла по каждой из поло-
вин арки
|
sк ~ |
2 |
(ϕ)ds |
π 2 2 |
sin |
2 |
ϕadϕ = 2a |
3 |
π 2 |
2 |
ϕdϕ = |
π |
a |
3 |
. |
|||
EIzδ11 = òM |
|
= 2 òa |
|
|
òsin |
|
2 |
|
||||||||||
|
0 |
|
|
|
0 |
π 2 |
|
|
|
0 |
|
|
|
|
|
|||
|
sк |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
||||
EIz 1P = òM P (ϕ)M |
(ϕ)ds = −2 ò0,5Pa(1− cosϕ)asin ϕadϕ = |
|
|
|||||||||||||||
|
0 |
|
π 2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Pa3 . |
|
|
|
|
|
|
|
|||
|
= −Pa ò(1− cosϕ)sin ϕdϕ = − |
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь из канонического уравнения определяем силу распора: |
|
|
|
|||||||||||||||
H = − |
1P = |
|
P |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
δ |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(30.9)
(30.10)
(30.11)
Статическая неопределимость раскрыта. Далее находим опорные реакции эквивалентной системы (см. рис. 30.5). Горизонтальная реакция в точке В тоже равна Н. Вертикальные, как и в случае на рис. 30.7, будут равны по 0,5Р. Когда

- 155 -
найдены опорные реакции, легко записать аналитические выражения для эпюр. Они отличаются от соотношений для случая на рис. 30.7 дополнительными сла- гаемыми от силы распора:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N(ϕ) = −0,5Pcosϕ − |
P |
asin ϕ , |
(30.12) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(ϕ) = 0,5Psin ϕ − |
P |
ϕ , |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
acos |
|
(30.13) |
|||||||
0,5P |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5P |
π |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M (ϕ) = 0,5Pa(1 − cosϕ) − |
P |
asin ϕ . (30.14) |
|||||||||||||||||||||||||
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
π |
|
|
||||||
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
Как и следовало ожидать, максимальные |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Рис. 30.11 |
|
|
|
|
|
|
|
изгибающие моменты в арке с распором |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 30.11 – |
30.12) оказываются более |
||||||||||||||||||||||||||||||||||||
Эпюра M z (ϕ) |
|
|
|
|
|
|
|
|
|
|
|
M z max = 0,181Pa |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
чем в два с половиной раза меньше, чем в |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
0,093Pa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,068Pa |
|
|
|
|
|
|
|
балке или в арке без распора. Перерас- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пределяются и внутренние силы N и Q |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,026Pa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 30.13 – 30.14). Значения на эпюрах |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,076Pa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
даны через каждые 15°. Указаны также |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,092Pa |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
экстремальные значения. |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
32,5° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,066Pa |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
В оболочках усилие распора может |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
Рис. 30.12 |
|
|
|
|
|
|
|
создавать сама оболочка, поэтому мо- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ментные зоны в оболочках часто локаль- |
|||||||||||||||||||||||||||||||||||||
Эпюра N (ϕ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,319P |
|
|
|
|
|
|
|
ны, т.е. занимают небольшую часть обо- |
|||||||||||||||||||||||||||||
|
0,593P |
|
0,437P |
|
|
|
|
|
|
|
лочки. Надо отметить, что именно эти не- |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
большие зоны обычно наиболее опасны |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,526P |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,578P |
|
|
|
|
|
|
|
|
|
для прочности оболочек, поэтому при про- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
32,5° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,566P |
|
|
|
|
|
|
|
ектировании |
и |
эксплуатации |
оболочек |
||||||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,500P |
|
|
|
|
B |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стремятся максимально уменьшить изгиб- |
||||||||||||||
|
|
|
|
|
|
|
|
|
Рис. 30.13 |
|
|
|
|
|
|
|
ные напряжения. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсутствие |
|
изгибных |
напряжений |
||||||||||||||||||||||||||||||||||
Эпюра Q(ϕ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
означает, что |
возникающие |
в |
оболочке |
|||||||||||||||||||
|
|
|
|
|
|
|
0,400P |
|
|
|
|
|
|
|
|
|
0,5P |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напряжения постоянны по толщине. Тео- |
||||||||||||||||||||||||||||||
|
0,273P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рия оболочек, построенная на этом пред- |
|||||||||||||||||||||
0,128P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0,5P |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
положении, |
называется |
|
безмоментной |
|||||||||||||||||||||||||||||||||||||||||
|
0,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
теорией оболочек. Следует отметить, что |
||||||||||
|
|
|
|
|
|
|
|
|
0,025P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чем меньше толщина оболочки, тем бли- |
||||||||||||
|
|
|
|
|
|
|
|
0,179P |
|
|
32,5° |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
A |
|
|
|
|
|
|
0,319P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,319P |
|
|
|
|
|
|
B |
же к истине предполагаемый закон по- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стоянства напряжений по толщине и тем |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Рис. 30.14 |
|
|
|
|
|
|
|
более точные результаты |
дает безмо- |
|||||||||||||||||||||||||||||||||||
ментная теория. Толщина оболочки должна быть значительно меньше её харак-

- 156 -
терных размеров. Расчёт оболочек более точными методами с учетом изгибаю- щих моментов показывает, что на достаточном удалении от перечисленных выше особых областей, в которых действуют моменты, определение напряже- ний может производиться по безмоментной теории. Определение же напряже- ний в моментных зонах, если они есть, требует проведения дополнительных расчётов.
Задача расчета безмоментных оболочек оказывается статически опреде- лимой в бесконечно малом, т.е. если внешняя нагрузка и находящиеся с ней в равновесии реакции опор известны, то внутренние погонные усилия Nx , N y ,
Nxy и напряжения в оболочке могут быть определены из одних дифференци- альных уравнений равновесия и граничных условий, чем мы воспользуемся.
|
|
|
|
O |
|
|
|
Рассмотрим далее некоторые, наибо- |
|||
|
|
|
|
|
|
лее простые задачи для осесимметричных |
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
оболочек вращения. |
Осесимметричными |
|||
|
A |
|
α |
O |
|
|
оболочками называются такие, срединная |
||||
|
|
|
|
поверхность |
которых |
представляет собой |
|||||
|
|
|
Ot |
Om |
поверхность вращения. Будем также пола- |
||||||
B |
|
|
OB |
гать, |
что нагрузка, действующая на такую |
||||||
|
|
|
оболочку, также обладает свойствами осе- |
||||||||
|
σm |
|
|
σm |
|||||||
|
|
OtB |
вой симметрии. Для таких оболочек задача |
||||||||
|
|
|
|
|
|
расчета значительно упрощается. Для не- |
|||||
|
|
|
Рис. 30.15 |
|
|
симметричных оболочек распределение на- |
|||||
|
m |
|
O |
dt |
пряжений определять значительно сложнее. |
||||||
|
|
|
|
Будем считать, что тонкая оболочка |
|||||||
|
|
|
|
|
|
|
|
||||
t |
|
|
|
|
вращения не имеет отверстия в области |
||||||
dm |
|
|
|
|
полюса и нагружена равномерным внеш- |
||||||
|
|
|
|
ним |
или |
внутренним |
давлением |
||||
|
(рис. 30.15), причём приложенное давле- |
|
|
ние уравновешивается нормальным на- |
|
|
пряжением σm , приложенным по торцу |
|
|
оболочки, представляющим собой кони- |
|
Рис. 30.16 |
ческое сечение. В качестве координат то- |
|
чек срединной поверхности используем, |
||
|
например, длины дуг меридианов m, измеряемые от полюса O (рис. 30.16), и длины дуг параллелей t, измеряемые от некоторого нулевого меридиана. Мери- дианы и параллели – обычные координатные линии для тел вращения.
В решении нам понадобятся радиусы кривизны срединной поверхности оболочки в сечениях по нормали к этой поверхности, проведённые в направле- нии координатных линий. Радиус кривизны сечения срединной поверхности,

- 157 -
проведённого через нормаль к этой поверхности в произвольной точке A и ме- ридиан этой точки, обозначим rm (отрезок AOm , рис. 30.15). Сечением будет,
очевидно, меридиан. Величина радиуса кривизны rm обусловлена формой ме-
ридиана – плоской кривой. Второй радиус кривизны срединной поверхности оболочки обозначим rt . Это радиус кривизны сечения, проходящего через две
пересекающиеся прямые: нормаль к срединной поверхности оболочки и каса- тельную к параллели в выбранной точке. Он направлен вдоль той же нормали к срединной поверхности оболочки и отличается от радиуса кривизны AO ок- ружности, которую образует параллель. Параллель также представляет собой плоскую кривую, её радиус кривизны AO обозначим r. Это не вполне очевидно, но в дифференциальной геометрии строго доказывается, что радиус кривиз- ны rt равен отрезку нормали AOt между произвольной точкой A и осью вра-
щения. Тогда очевидно, что между радиусом кривизны параллели и радиусом
кривизны нормального сечения существует зависимость
r = rt cosα . |
|
|
|
|
(30.15) |
||||
|
sdF |
|
|
|
|
|
|
|
Отметим ещё, что радиусы кривиз- |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ны нормальных сечений для выбранных |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
координатных линий являются главными, |
|
α |
|
|
|
|
|
|
||
s |
|
|
|
|
|
|
т.е. это наибольший и наименьший ради- |
||
|
|
x F |
|
||||||
|
|
||||||||
dF |
|
|
|
ус кривизны нормальных сечений сре- |
|||||
|
|
|
|
|
|
x |
|
динной поверхности оболочки в данной |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точке, что показывается в дифференци- |
|
F |
|
|
|
|
||||
|
|
|
|
|
альной геометрии. Такие линии называ- |
||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 30.17 |
|
|
|
|
ются линиями главных кривизн или ли- |
|||
|
|
|
|
|
ниями кривизны. Линии кривизны в одной |
||||
|
|
|
|
|
|
|
|
|
|
точке всегда оказываются ортогональными. Уравнения для расчёта произволь- ных оболочек с координатными линиями, совпадающими с линиями кривизны, записываются несколько проще и потому чаще используются. Тем более есте- ственно рассмотрение оболочек вращения в таких координатах.
Докажем теперь несложную теорему.
Теорема. Если на поверхность действует равномерно распределенное давление s, то независимо от формы поверхности проекция равнодействующей сил давления на заданную ось равна произведению давления на площадь проек- ции поверхности на плоскость, перпендикулярную к заданной оси.
Доказательство. Предположим, задана поверхность F (рис. 30.17), на которую действует равномерно распределенное давление s по нормали к по- верхности. Требуется определить проекцию на направление оси x равнодейст- вующей сил давления. Эта проекция Px будет, очевидно, равна интегральной

- 158 -
сумме проекций на направление оси x всех сил, приложенных к элементарным площадкам dF:
Px = òscosα dF , |
(30.16) |
F |
|
постоянное давление можно вынести за знак интеграла, а умножение элемента площади dF на cosα даёт площадь проекции dFx этого элемента на плоскость,
перпендикулярную оси x:
dFx = dF cosα . |
(30.17) |
Тогда |
|
Px = s òdFx = sFx . |
(30.18) |
F |
|
Таким образом, для того чтобы определить проекцию равнодействующей сил давления на направление оси, нужно предварительно спроектировать по- верхность на плоскость, перпендикулярную оси, а затем умножить давление на площадь этой проекции, что и требовалось доказать.
|
σmhdt |
dϕt |
|
Получим теперь одно из уравнений |
||
σthdm |
rt |
|
равновесия |
бесконечно малого элемента |
||
|
|
оболочки. По методу сечений двумя парами |
||||
|
|
|
||||
sdmdt |
|
Ot |
Om |
меридиональных и нормальных конических |
||
σthdm |
сечений (см. рис. 30.16) выделим из оболоч- |
|||||
|
|
|||||
|
|
ки элемент со сторонами dm и dt, изобра- |
||||
|
|
rm dϕm |
|
жённый также отдельно на рис. 30.18. На |
||
|
σmhdt |
|
|
гранях элемента могут возникать напряже- |
||
|
|
|
ния σm и σt . Первое будем называть мери- |
|||
|
Рис. 30.18 |
|
диональным |
напряжением. Вектор этого |
||
напряжения направлен по касательной к дуге меридиана. Второе напряжение σt на-
зовём окружным напряжением. Других напряжений на рассматриваемых площад- ках не будет. Действительно, касательные напряжения τmt в осесимметричной зада-
че появиться не могут, они противоречат условиям симметрии. Касательные же на- пряжения τmz и τtz , связанные с перерезывающими силами в оболочке, считаем ну-
левыми в безмоментной оболочке. Напряжения σm и σt , умноженные на соответст- вующие площади граней элемента, дадут силы σmhdt и σthdm (см. рис. 30.18). К
этому же элементу приложена сила нормального давления sdmdt . Просуммировав проекции всех этих сил на нормаль, из условия равновесия получим
sdmdt − 2σm hdt sin |
dϕm |
− 2σt hdmsin |
dϕt |
= 0 , |
(30.19) |
|
2 |
||||
2 |
|
|
|
||
но синус бесконечно малого угла равен самому углу, поэтому |
|
||||
sdmdt − σmhdtdϕm − σthdmdϕt = 0 , |
|
|
(30.20) |
||
откуда

|
σm |
|
|
|
|
|
|
|
|
σt |
- 159 - |
|
||||
|
|
|
|
|
+ |
|
|
|
= |
s |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
. |
(30.21) |
||||
|
dm dj |
m |
dt dj |
|
h |
|||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|||||
Здесь отношения длин дуг к центральным углам дают радиусы кривизны |
|
|||||||||||||||
dm dϕm = rm , dt dϕt = rt . |
(30.22) |
|||||||||||||||
В результате получаем |
|
|||||||||||||||
|
σm + |
σt |
= |
s |
. |
|
|
|
|
(30.23) |
||||||
|
|
|
|
|
|
|||||||||||
|
r |
|
r |
|
|
|
h |
|
|
|
|
|
||||
|
m |
|
|
t |
|
|
|
|
|
|
|
|
|
|
||
Это уравнение называется уравнением Лапласа. |
|
|||||||||||||||
Из формул (30.2), где в безмоментной оболочке Mm = Mt = Mmt = 0, сле- |
||||||||||||||||
дует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Nm = σmh, Nt = σth, Nmt = τmth , |
(30.24) |
||||||||||||||
тогда уравнение Лапласа можно переписать по-другому: |
|
|||||||||||||||
|
Nm |
+ |
|
Nt |
|
= s . |
|
|
|
|
(30.25) |
|||||
|
|
|
|
|
|
|
|
|||||||||
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
||
|
m |
|
|
t |
|
|
|
|
|
|
|
|
|
|
||
Применим доказанную теорему к части оболочки вращения, отсеченной коническим сечением вдоль параллели и содержащую полюс (см. рис. 30.15). Равнодействующая сил внутреннего давления, направленная вдоль оси оболоч- ки, уравновешивается составляющей силой от меридиональных напряже- ний σm , действующих на коническое сечение, проведённое по параллели:
spr2 = sm 2prhcosa , |
(30.26) |
||||||||||
откуда можно найти нормальное напряжение σm : |
|
||||||||||
sm = |
|
|
|
r |
|
s , |
(30.27) |
||||
2hcosa |
|||||||||||
|
|
|
|
|
|||||||
учтя (30.15), получим окончательно |
|
||||||||||
sm = |
|
rt |
|
s . |
|
|
|
|
(30.28) |
||
|
2h |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
Теперь из уравнения Лапласа в форме (30.23) определяется и окружное |
|||||||||||
напряжение σt : |
|
|
|
|
|
||||||
æ |
|
|
|
rt |
ö rt |
|
|||||
ç |
|
|
|
|
÷ |
|
|
(30.29) |
|||
|
|
|
2r |
|
|||||||
st = ç1- |
|
÷ h s . |
|||||||||
è |
|
|
|
m ø |
|
||||||
Едва ли не чаще оболочек вращения сложной формы в технике исполь- зуются оболочки частного вида: сферические, конические и цилиндрические. Для сферической оболочки (рис. 30.19) rm = rt = r , поэтому из формул (30.28 –
30.29) найдём, что окружное и меридиональное напряжения равны: |
|
|||
sm = st |
= |
r |
s . |
(30.30) |
|
||||
|
|
2h |
|
|
Если в |
замкнутой у полюса оболочке, например баллоне |
давления |
||

- 160 - (рис. 30.20), есть цилиндрическая часть, то rm = ∞ , rt = r , тогда
σm = 2rh s , σt = hr s ,
откуда
σt = 2σm ,
У конической оболочки (рис. 30.21) rm
σm = 2rht s , σt = rht s ,
σ |
r = rt |
s |
|
σ |
|
|
r = rm = rt |
в цилиндрической части оболочки
(30.31)
(30.32)
= ∞ , тогда
(30.33)
r = rm = rt
s 
rt 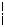 s
s
 σm
σm  σm
σm
Рис. 30.19 Рис. 30.20 Рис. 30.21
так что и для этой оболочки справедливо равенство (30.32). Но в конической обо- лочке есть особая моментная точка у полюса (рис. 30.21). На эту точку и её окре- стность полученное решение не распространяется. Особую точку можно исклю- чить, завершив оболочку, например, сферой. Тогда полученные формулы будут справедливы для сферической и конической частей оболочки. Радиус кривизны является одним из характерных размеров оболочки, поэтому радиус сферы дол- жен значительно превышать толщину оболочки, иначе её нельзя будет считать тонкой.
Таким образом, в цилиндрических и конических безмоментных оболочках, нагруженных равномерным наружным или внутренним давлением, окружное напряжение в два раза больше меридионального. Это свойство называют законом сосисок, которые, если их переварить, лопаются, как известно, вдоль оси из-за вдвое больших растягивающих нормальных напряжений в окружном направлении.
Аналогично можно записать напряжения и для любой составной осесиммет- ричной оболочки вращения под действием внутреннего или внешнего давления.
