
Lectures part2
.pdf∂M z (x) |
|
- 21 - |
= f (x) . |
(18.5) |
|
¶P |
|
|
Так как каждое слагаемое в формулах (18.3), (18.4) представляет собой эпюру от силового фактора, то функция 1× f (x) представляет собой, очевидно,
эпюру в рассматриваемой конструкции от силы P, равной единице. Обозначив
~ =
P 1 единичную силу того же направления и приложенную в той же точке, что
и P, запишем |
|
~ |
× f (x). |
(18.6) |
||
|
|
|
||||
f (x)=1× f (x)= P |
||||||
Для эпюры от единичного силового фактора введём обозначения: |
|
|||||
~ |
~ |
× f (x) . |
|
|
(18.7) |
|
M z |
(x)= P |
|
|
|||
По-другому обозначим частную производную от изгибающего момента: |
|
|||||
~ * |
(x)= f |
(x)= |
∂M z (x) |
. |
(18.8) |
|
M z |
|
¶P |
||||
|
~ |
|
~ |
|
|
|
|
|
* |
|
|
||
Величины M z (x) и |
M z (x) численно равны, но размерность у них разная. Раз- |
|||||
мерность производной момента есть, конечно, размерность момента, делённого на силу [Н × м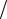 Н = м], т.е. метры. Размерность же момента от единичной силы
Н = м], т.е. метры. Размерность же момента от единичной силы
обычная для эпюры моментов [Н ×м]. |
|
|
|||
Аналогичный результат получится и для производной: |
|
|
|||
~* |
(x)= |
∂N(x) |
|
|
|
N |
¶P |
. |
|
(18.9) |
|
|
|
|
~ |
(x) |
имеет обыч- |
Сама производная будет безразмерной, а эпюра осевых сил N |
|||||
ную размерность силы.
Учитывая численное равенство этих величин, далее в формулах не будем
|
|
|
|
|
|
|
~ |
|
~ * |
~ |
~* |
(x). |
делать различий между величинами M z (x) и |
M z (x), |
N |
(x) и N |
|||||||||
Поэтому с учётом принятых обозначений формула для определения пе- |
||||||||||||
ремещений точек в плоской стержневой конструкции (18.2) принимает вид: |
||||||||||||
|
|
~ |
(x) |
|
~ |
|
|
|
|
|
|
|
j=n |
é N(x)N |
|
M z (x)M z (x)ù |
|
|
|
|
|||||
D = å ò |
ê |
|
|
|
+ |
|
|
ú dx . |
|
|
|
(18.10) |
EF |
|
|
EIz |
|
|
|
|
|||||
j=1 l j |
ë |
|
|
|
|
û j |
|
|
|
|
||
Полученная формула называется интегралом Мора.
В плоских задачах для рам энергия растяжения-сжатия обычно оказыва- ется значительно меньше энергии изгиба, поэтому для плоских рам часто (но не всегда) можно использовать интеграл Мора всего с одним слагаемым.
j=n |
|
é |
~ |
ù |
|
|
|
|
M z (x)M z (x) |
|
|
||||
D = å ò |
ê |
ú |
dx . |
(18.11) |
|||
EIz |
|||||||
j=1 |
l j |
ë |
û j |
|
|
||
Форма записи интеграла Мора для общего случая нагружения при учёте поперечных сдвигов очевидна:
j=n
D = å
j=1
|
|
~ |
|
|
|
|
|
|
|
~ |
- 22 - |
|
|
|
~ |
|
|
|
|
|
|
|
||||
|
|
(x) |
|
Qy |
|
(x) |
|
Q |
|
|
|
|
(x) |
|
|
|
|
|||||||||
é N(x)N |
|
(x)Qy |
|
(x)Q |
z |
|
|
|
|
|||||||||||||||||
ò ê |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
z |
|
|
|
|
|
|
+ |
|
|
|
|
|
EF |
|
|
|
|
|
|
GF |
|
|
|
|
|
GF |
|
|
|
|
|
|
||||||
l j ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ë |
|
|
~ |
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
~ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ |
M x (x)M x (x) |
+ |
|
M y (x)M y (x) |
+ |
M z (x)M z (x)ù |
dx . |
(18.12) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|||||||
GI p |
|
|
|
|
|
EI y |
|
|
|
|
|
EIz |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û j |
|
|
Напомним, что полученный интеграл Мора представляет собой выражение тео- ремы Кастильяно для стержневой конструкции.
Порядок расчета перемещений с помощью интеграла Мора
Определить обобщённое перемещение в одной из точек стержневой кон- струкции можно с помощью интеграла Мора следующим образом:
1.Получить выражения для эпюр от основной нагрузки стержневой кон- струкции.
2.Приложить к конструкции без основной нагрузки в точке, где требует- ся определить перемещение, единичную нагрузку в направлении искомого пе- ремещения.
3.Получить выражения для эпюр от единичного нагружения.
4.Записать и вычислить интеграл Мора.
Замечания а) если значение перемещения получается со знаком плюс, но направле-
ние перемещения совпадает с направлением единичного силового фактора, ес- ли же оно получается со знаком минус, то направление перемещения противо- положно этому фактору;
б) как и при использовании теоремы Кастильяно, наличие сосредоточенного силового фактора в точке, где необходимо определять перемещение, не обязательно; в) излом или разрыв хотя бы одной из эпюр вынуждает вводить границу
участка для всех эпюр, входящих в интеграл Мора;
г) координаты x на всех эпюрах надо отсчитывать одинаково, т.е. от одно- го начала и в одном направлении.
Пример. В раме на рис. 18.1 необходимо определить полное перемещение точки A и угол поворота поперечного сечения в этой точке, предполагается что EIz = const . Для определения полного перемещения точки A найдём две состав- ляющие этого перемещения: A гор – горизонтальное перемещение точки A, и
Aверт – вертикальное перемещение этой точки. Воспользуемся упрощенной
формой записи интеграла Мора в плоской задаче (18.11). Это оправданно при равных длинах обоих стержней. Если бы длина стержня BC была малой, много меньше длины стержня AB, то пренебрегать энергией от сжатия стержня AB было бы нельзя.
|
|
|
|
|
- 23 - |
|
|
|
|
|
Применим предложенный выше порядок действий (алгоритм). При по- |
||||||||
строении эпюр в раме рассматриваем два участка: AB и BC. Направления отсчёта |
|||||||||
координат x, используемые для всех эпюр, показаны на рисунке двойными стрел- |
|||||||||
|
|
|
|
ками. Эпюра изгибающих моментов от основного на- |
|||||
|
C |
|
|
гружения M z (x) изображена на рис. 18.1. Для опре- |
|||||
a |
|
|
|
деления |
A гор |
прикладываем горизонтальную |
еди- |
||
|
B |
A |
P |
|
~ |
, как показано на рис. 18.2. Получаю- |
|||
|
ничную силу P1 |
||||||||
|
|
a |
|
|
|
|
|
~ |
|
|
|
|
щаяся эпюра от единичного нагружения M z1(x) пред- |
||||||
Эпюра M z (x), кН ×м |
ставлена на этом же рисунке. Для определения |
A верт |
|||||||
прикладывается |
~ |
и определяется соответст- |
|||||||
8 |
C |
|
|
сила P2 |
|||||
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
вующая эпюра моментов M z2 (x) (рис. 18.3). Для на- |
|||||
|
B |
A |
|
хождения угла поворота в точке A в этой точке при- |
|||||
|
|
кладывается единичный момент и также определяется |
|||||||
|
|
|
|
||||||
|
Рис. 18.1 |
|
|
|
|
~ |
(x) (рис. 18.4). |
||
|
|
соответствующая эпюра моментов M z3 |
|||||||
|
C |
|
|
C |
|
~ |
C |
~ |
|
|
|
|
~ |
|
|
|
|
||
|
|
|
|
|
P2 |
|
M 3 |
|
|
|
|
|
P1 |
|
|
|
|
|
|
|
B |
|
A |
B |
|
A |
B |
A |
|
~ |
~ |
(x), кН × м |
~ |
(x), кН ×м |
Эпюра M z1(x), кН × м |
Эпюра M z2 |
Эпюра M z3 |
2 |
C |
|
|
C |
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
A |
|
B |
2 |
A |
|
|
B |
1 |
A |
|
Рис. 18.2 |
|
|
Рис. 18.3 |
|
|
|
Рис. 18.4 |
|
||
|
Для участка AB аналитические выражения для этих эпюр следующие: |
||||||||||
|
M z (x1 )= 0, |
~ |
(x1 )= 0, |
~ |
~ |
|
, |
~ |
~ |
, |
(18.13) |
|
M z1 |
M z2 (x1 )= -P2 x1 |
M z3 |
(x1 )= -M3 |
|||||||
Для участка BС: |
~ |
|
~ |
~ |
~ |
~ |
|
~ |
, |
. (18.14) |
|||||
M z (x2 )= Px2 , M z1 |
(x2 )= P1 x2 |
M z2 |
(x 2 )= -P2 a, |
M z3 |
(x 2 )= -M3 |
Теперь с помощью интегралов Мора определяются искомые горизонталь- ное и вертикальное перемещения точки A:
j=2
DA гор = å j=1
|
éM |
|
~ |
|
(x)ù |
|
1 æ |
a |
ö |
|
Pa |
3 |
|
|
|||
|
z |
(x)M |
z1 |
|
|
|
|
|
|
||||||||
ò |
ê |
|
|
|
ú |
dx = |
|
ç0 |
+ ò(Px × x)dx÷ |
= |
|
|
, |
(18.15) |
|||
|
|
|
|
|
|
|
|
||||||||||
l j |
ë |
|
|
EIz |
|
|
û j |
|
EIz è |
0 |
ø |
|
3EIz |
|
|
||

|
|
|
|
|
~ |
|
(x)ù |
- 24 - |
|
|
|
|
|
|
|
||
j=2 |
|
éM |
|
|
|
1 |
æ |
a |
ö |
|
Pa |
3 |
|
||||
|
z |
(x)M |
z 2 |
|
|
|
|
|
|||||||||
DA верт = å ò |
ê |
|
|
|
ú |
dx = |
|
ç0 |
+ ò [Px × (- l)]dx÷ |
= - |
|
|
. (18.16) |
||||
|
|
EIz |
|
|
|
2EIz |
|||||||||||
j=1 |
l j |
ë |
|
|
|
|
û j |
|
EIz è |
0 |
ø |
|
|
||||
Полученный знак «плюс» у горизонтального перемещения означает, что оно
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
происходит в направлении |
единичной |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
силы P1 (рис. 18.2); Знак «минус» – дан- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
ное перемещение происходит вниз в на- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
правлении, |
противоположном |
~ |
|
|
|
|
|
|
|
|
|
|
|
Рис. 18.5 |
|
|
|
|
|
|
силе P2 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полное перемещение находится как век- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
тор по его проекциям на взаимно пер- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пендикулярные направления (по теореме |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
qл |
qп |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пифагора): |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = |
D2A гор + D2A верт |
. |
(18.17) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно определить и направление полно- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
го перемещения с помощью какой-либо |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
тригонометрической функции одного из |
||||
|
|
|
|
|
|
|
|
|
|
Рис. 18.6 |
|
|
|
|
|
|
острых углов прямоугольного треуголь- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ника, образующегося при проектирова- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нии полного перемещения на эти направления, например: |
|
|||||||||||||||||||||||||||
|
|
tga = |
|
DA гор |
|
. |
|
|
|
|
|
|
|
|
|
|
|
(18.18) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
DA верт |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Угол поворота сечения в точке A запишется так |
|
|
|||||||||||
j=2 |
éM |
|
~ |
|
(x)ù |
|
1 æ |
a |
ö |
|
|||
z |
(x)M |
z3 |
|
|
|
||||||||
θA = å ò |
ê |
|
|
|
ú |
dx = |
|
ç0 |
+ ò [Px × (-1)]dx÷ |
= - |
|||
|
|
EIz |
|
|
|
||||||||
j=1 l j |
ë |
|
|
|
|
û j |
|
EIz è |
0 |
ø |
|
||
Pa2 . (18.19) 2EIz
~ |
|
Заметим вновь, что размерность |
||
M л =1 |
|
силы и момента эпюр от единичной силы |
||
|
|
и момента в интеграл Мора включать не |
||
|
|
|||
A |
|
следует, это не соответствует формуле |
||
~ |
=1 |
Мора и нарушит размерность результата. |
||
Входят только числовые множители при |
||||
M п |
||||
|
|
них. При вычислении угла поворота |
||
A |
|
множитель (−1) безразмерный. Множи- |
||
|
~ |
~ |
||
Рис. 18.7 |
|
тели M z1 |
и M z2 имеют размерность дли- |
|
|
ны. |
|
||
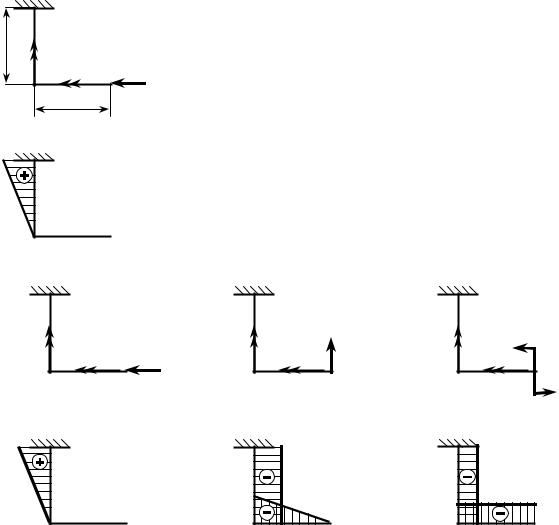
При проведении практических расчётов часто приходится вычислять вза- имные перемещения точек, т.е. определять, насколько сблизятся или разойдут-
ся отдельные точки конструкции или насколько повернутся относительно друг

- 25 -
друга поперечные сечения конструкции, например соседние сечения около
шарнира в конструкции на рис. 18.5. |
Взаимный угол поворота соседних |
|
~ |
~ |
|
Mл =1 |
Mп =1 |
поперечных сечений θ в точке A изо- |
|
|
бражён на рис. 18.6. Он, как видно из ри- |
A |
|
сунка, складывается из углов поворота |
|
крайнего сечения части балки слева θл и |
|
|
|
|
Рис. 18.8 |
|
справа θп от шарнира. Эти углы поворо- |
|
|
та определяются с помощью интегралов |
Мора, для чего прикладываются поочерёдно два единичных противоположно направленных момента (рис. 18.7) и определяются эпюры моментов от этих на- грузок (индекс z у изгибающих моментов для краткости писать не будем), а за-
тем вычисляется интеграл Мора: |
|
|
|
~ |
|
|
|
||||
|
|
~ |
(x)ù |
|
|
|
|
|
|
||
j=n |
éM(x)Mл |
j=n |
|
éM(x)Mп (x)ù |
|
|
|||||
q = qл + qп = å ò ê |
|
|
ú |
dx + å ò |
ê |
|
ú |
dx . |
(18.20) |
||
EIz |
|
EIz |
|||||||||
j=1 |
lj ë |
|
û j |
j=1 |
lj |
ë |
û j |
|
|
||
Здесь интегралы вычисляются по участкам одной и той же конструкции, поэтому их можно объединить. Сумма единичных эпюр представляет собой по принципу
~ ( )
суперпозиции эпюру от одновременного действия единичных сил Mлп x :
j=n
q = qл + qп = å
j=1
j=n
= å
j=1
|
|
|
~ |
|
|
~ |
(x)} |
|
|
|
é |
|
M(x){Mл (x)+ Mп |
|
|||||
ò |
|
|
|
|
|
ù |
dx = |
||
ê |
|
|
|
|
|
|
ú |
||
|
EIz |
|
|
||||||
lj |
ë |
|
~ |
|
|
û j |
|
||
|
|
|
лп (x)ù |
|
|
|
|
||
ò |
éM (x)M |
dx . |
(18.21) |
||||||
ê |
|
|
|
ú |
|||||
|
EIz |
|
|||||||
l j |
ë |
|
|
û j |
|
|
|
|
|
~ ( )
Для получения эпюры Mлп x можно прикладывать к конструкции одно- временно два единичных момента (рис. 18.8). Отсюда очевидно следующее ут-
верждение: для определения взаимных обобщённых перемещений точек конст-
A |
|
|
B |
~ |
=1 |
~ |
=1 |
рукции следует вычислить интеграл Мо- |
||||||
|
|
P |
P |
|||||||||||
|
|
|
|
|
|
|
|
|
A |
B |
|
|
|
ра для эпюры от нагрузки конструкции и |
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
эпюры от одновременно приложенных к |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
этим точкам двух противоположно на- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
правленных обобщённых единичных сил. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В качестве ещё одного примера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 18.9 |
|
|
|
|
укажем, что для определения взаимного |
|||
|
|
|
|
|
|
|
|
|
|
перемещения точек A и B от силы Р в ра- |
||||
ме на рис. 18.9 следует найти аналитические выражения для эпюр от силы Р и эпюр от единичного нагружения двумя противоположными единичными сила-
~
ми P , показанными на рисунке, а затем вычислить интеграл Мора.
|
|
|
|
|
|
|
|
|
|
|
|
|
- 26 - |
|
|
|
|
|
|
|
|
Способ Верещагина для вычисления интеграла Мора |
|
||||||||||||||||
Если конструкция состоит из прямых стержней, то эпюры от единичных |
|||||||||||||||||||
сил и моментов оказываются прямолинейными. Тогда интеграл Мора можно |
|||||||||||||||||||
вычислить с помощью площадей эпюр, которые и есть соответствующие инте- |
|||||||||||||||||||
гралы, но формулы для вычисления этих интегралов просты и известны. Рас- |
|||||||||||||||||||
смотрим получение формулы способа Верещагина. |
xн ≤ x ≤ xк |
|
|||||||||||||||||
Считаем, |
|
что |
изгибная |
жёсткость |
на |
участке |
постоян- |
||||||||||||
на ( EIz = const ). Линейная эпюра моментов от единичного нагружения может |
|||||||||||||||||||
быть описана соотношением |
|
|
|
|
|
|
|
|
|
||||||||||
~ |
|
|
+ bx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(18.22) |
||
M (x)= a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда интеграл Мора на данном участке примет вид: |
|
|
|||||||||||||||||
|
xк é |
|
~ |
ù |
|
|
xк é |
|
|
|
ù |
|
|
|
|
||||
i = ò |
êM (x)M (x)údx |
= ò |
êM (x)(a + bx)údx = |
|
|
|
|||||||||||||
|
xн ë |
EIz |
|
û |
|
|
xн ë |
|
EIz |
|
û |
|
|
|
|
||||
|
|
|
|
|
|
|
|
a |
|
x |
|
|
b |
|
x |
|
|
|
|
|
|
|
|
|
|
= |
|
|
òкM (x)dx + |
|
òк x M (x)dx . |
|
(18.23) |
||||||
|
|
|
|
|
|
|
EI |
z xн |
|
|
EI |
z |
xн |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
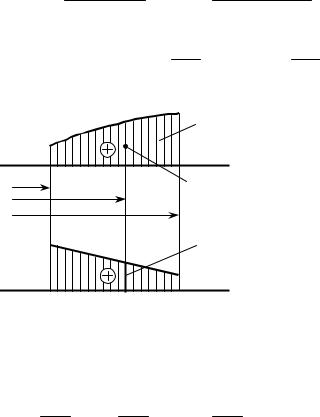
Эп. M (x) |
|
|
|
|
|
|
|
|
|
FM |
|
|
|
|
Первый из интегралов представляет |
||||
|
|
|
|
|
|
|
|
|
|
собой, как всякий определённый интеграл, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
xн |
|
|
|
|
|
|
|
|
|
|
|
|
площадь |
под эпюрой M (x); |
обозначим |
||||
|
x |
|
|
|
|
|
|
ц.т. |
|
её FM (рис. 18.10). Второй интеграл есть ста- |
|||||||||
|
|
|
с |
|
|
xк |
|
|
|
|
|
|
тический момент той же площади относи- |
||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
~ |
|
тельно вертикальной оси у той же системы |
|||||||
Эп. M (x) |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
координат, обозначим этот статический мо- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
мент SM и представим его себе в виде про- |
||||||
|
|
Рис. 18.10 |
|
|
|
|
|
|
изведения площади фигуры на координату её |
||||||||||
|
|
|
|
|
|
|
|
центра тяжести xc : |
|
|
|||||||||
SM = FM xc . |
|
|
|
|
|
|
|
|
|
(18.24) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда |
|
a F |
|
|
b |
|
|
|
|
|
= FM |
|
|
|
|
|
|
|
|
i = |
|
|
+ |
F |
|
x |
c |
|
(a + bx ) . |
|
|
|
(18.25) |
||||||
|
|
M |
|
|
M |
|
|
EIz |
|
c |
|
|
|
|
|
||||
|
EIz |
|
|
EIz |
|
|
|
|
|
|
|
|
|
|
|
||||
Величина в скобках представляет собой одно из значений эпюры от единичного |
|||||||||||||||||||
нагружения (18.22) – это значение единичной эпюры под центром тяжести ос- новной (значение единичной эпюры для координаты центра тяжести xc основ-
ной эпюры на участке). Обозначим его:
~ |
|
ˆ |
(18.26) |
M = a + bxc . |
Тогда
|
~ |
|
|
|
|
|
|
- 27 - |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = |
FM M , |
|
|
|
|
|
|
|
|
|
|
|
(18.27) |
|||
|
EIz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда следует, что интеграл Мора переписывается так: |
|
|
|
|||||||||||||
|
j=n |
|
é |
|
~ |
ù |
j=n |
é |
|
~ |
ù |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
. |
|
(18.28) |
|||||||
D = å ò |
êM z |
(x)M z (x)ú |
dx = å |
êFM M |
ú |
|
||||||||||
|
j=1 l |
|
ë |
EI |
z |
|
û j |
j=1 |
ê |
EI |
z |
ú |
|
|
|
|
|
|
j |
|
|
|
ë |
|
û j |
|
|
|
|
||||
Здесь интеграл заменен площадью основной эпюры моментов, которая умно- |
||||||||||||||||
жается на значение единичной эпюры под центром тяжести основной эпюры |
||||||||||||||||
моментов. Это формула и представляет собой способ Верещагина для вычисле- |
||||||||||||||||
ния интеграла Мора. |
|
|
|
|
|
|
|
|
~ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что вычисление произведения |
ˆ |
|
|
|
||||||||||||
FM M называют перемножением |
||||||||||||||||
эпюр и что способом Верещагина удобно пользоваться при относительно про- |
||||||||||||||||
стых эпюрах моментов, когда известны формула для площади эпюры и поло- |
||||||||||||||||
жение её центра тяжести. При более сложных эпюрах удобнее вычислять непо- |
||||||||||||||||
средственно интеграл Мора. |
|
|
|
|
|
|
|
|
|
|||||||
|
Порядок расчета с использованием способа Верещагина |
|
|
|||||||||||||
Поскольку способом Верещагина вычисляется тот же самый интеграл |
||||||||||||||||
Мора, то принципиальных отличий от порядка расчета по Мору, конечно, нет. |
||||||||||||||||
A |
|
|
B |
|
|
|
|
С |
Однако соответствующие эпюры необхо- |
|||||||
|
|
|
|
|
|
димо строить, а не только записывать их |
||||||||||
|
l |
|
|
P |
|
l |
|
|
||||||||
|
|
|
|
|
|
аналитические выражения. Пункт 4 алго- |
||||||||||
|
2 |
|
|
|
|
2 |
|
|
ритма расчёта перемещений с помощью |
|||||||
Эп. M (x) |
|
ц.т. |
|
|
|
|
интеграла Мора следует сформулировать |
|||||||||
|
|
|
|
|
иначе: |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
4) Перемножить эпюры на каждом |
||||
2 |
l |
|
|
|
|
|
Pl |
|
участке, |
разделить на изгибную |
|
жёст- |
||||
3 × |
2 |
|
Mmax |
|
= |
|
кость сечения на данном участке, а ре- |
|||||||||
|
|
|
|
|
|
|
4 |
|
зультаты сложить. |
|
|
|
||||
|
Рис. 18.11 |
|
|
|
|
|
|
Поскольку |
непосредственно |
вы- |
||||||
|
|
|
|
|
|
|
|
|
числять интегралы не нужно, то замеча- |
|||||||
ния «в» и «г» можно снять, заменив их новыми: |
|
|
|
|||||||||||||
в*) площадь эпюры и момент под центром тяжести следует подставлять в |
||||||||||||||||
формулу со своим знаком; |
|
|
|
|
|
|
|
|
|
|||||||
г*) площадь эпюры следует брать из эпюры от основного нагружения |
||||||||||||||||
конструкции, а момент от под центром тяжести – из прямолинейной эпюры от |
||||||||||||||||
единичного нагружения, и только если обе эпюры прямолинейные, то они рав- |
||||||||||||||||
ноправны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-28 -
Впоследнем случае берётся площадь любой из эпюр (от основного или единичного нагружения) и умножается на значение второй эпюры под центром тяжести первой, с которой взята площадь.
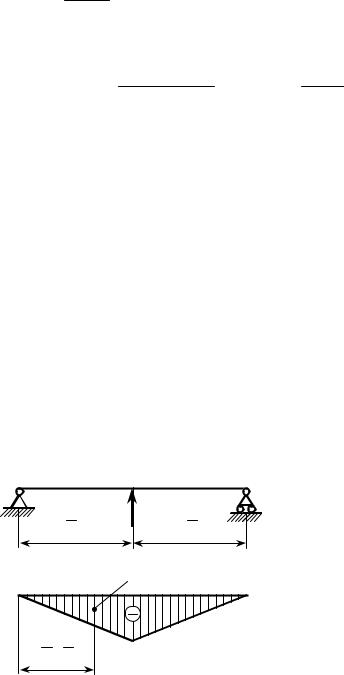
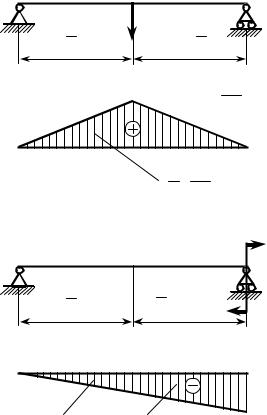
Пример. Для балки на рис. 18.11 требуется определить прогиб в середине пролёта балки (в точке B) и угол поворота её сечений над опорами (в точках A
иС).
Всоответствии с порядком расчёта по способу Верещагина строим эпю-
A |
B |
|
|
С |
l |
~ |
|
l |
|
2 |
P |
=1 |
2 |
~ |
~ |
|
~ |
|
|
|
= |
Pl |
||
Эп. M1(x) |
M1 max |
4 |
||
|
|
|
|
|
|
|
|
|
~ |
|
|
2 |
× |
Pl |
|
|
3 |
|
4 |
|
|
Рис. 18.12 |
|
|
A |
|
B |
|
С |
|
l |
l |
~ |
|
|
2 |
2 |
M =1 |
|
~ |
(x) |
|
|
|
Эп. M2 |
|
|
|
|
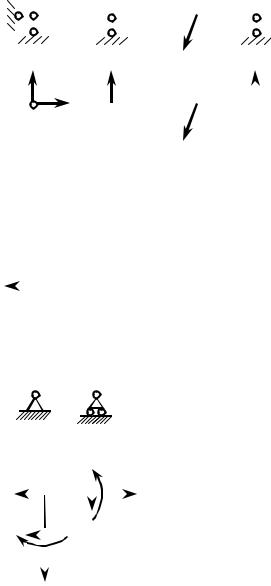
ры от основного нагружения (рис. 18.11), от единичной силы, приложенной верти- кально в точке B (рис. 18.12), и единич- ного момента, приложенного в точке С (рис. 18.13). В силу симметрии задачи
углы поворота поперечных сечений в точках A и С равны. Далее находим ис-
комые величины с помощью формулы Верещагина. Размерную единицу силово- го фактора вновь не включаем в форму- лы, как и при использовании непосредст- венно интеграла Мора. Учитываем, что
при вычислении прогиба получается два одинаковых слагаемых
D |
|
= |
2 |
éæ |
- |
1 Pl l öæ |
2 l öù |
= |
|||||
B |
|
ç |
|
|
֍ |
|
|
÷ |
ú |
||||
|
|
|
|||||||||||
|
|
|
ê |
|
2 4 2 øè |
|
|
|
|
||||
|
|
|
EIz ëè |
|
3 4 øû |
|
|||||||
= - |
Pl3 |
|
|
|
. |
(18.29) |
|
|
|||
|
48EIz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
=1 |
|
Здесь площадь эпюры моментов берётся со |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
M2 max = M |
|
знаком «минус». Прогиб получается отри- |
||||||||||||||||||
|
|
|
|
|
|
|
|
Рис. 18.13 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цательным, поскольку в данной задаче оче- |
||||||||||||||||
видно, что точка B перемещается вверх, а не в сторону приложенной единичной си- |
||||||||||||||||||||||||||||||
лы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pl2 |
|
||
|
|
|
|
2 |
|
éæ |
|
1 Pl l öæ |
2 |
|
1 öù |
|
2 éæ |
|
1 |
|
Pl |
|
l |
öæ |
|
2 |
öù |
|
|
|||||
qC |
= |
|
|
êç |
- |
|
|
֍- |
|
× |
÷ú |
+ |
|
êç |
- |
|
× |
|
× |
|
֍ |
- |
|
×1÷ú = |
|
|
. |
(18.30) |
||
|
|
|
3 |
|
2 |
4 |
2 |
3 |
|
|||||||||||||||||||||
|
|
|
|
EIz ëè |
|
2 4 2 øè |
|
2 øû |
|
EIz ëè |
|
|
|
øè |
|
øû |
16EIz |
|
||||||||||||
Действительное направление угла поворота сечения в точке С совпадает, очевидно, с направлением единичного момента, в чём убеждаемся, получив ре- зультат со знаком «плюс».
- 29 -
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ
Тема №19. Понятие статической неопределимости. Степень статиче-
ской неопределимости
Понятие статической неопределимости
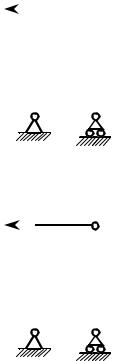
Вполне очевидно, что балки могут иметь более сложные опоры, чем те, которые до сих пор рассматривались. Например, шарнирных опор может быть
|
|
|
A |
|
|
B |
|
|
С |
три и больше (рис. 19.1). Уже при одной |
|||||
|
|
|
|
|
|
|
дополнительной опоре опорные реакции |
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
невозможно определить методами теоре- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тической механики, т.е. из уравнений |
|
|
|
|
|
|
R1 |
R2 |
|
|
R3 |
|
|
||||
|
|
|
|
|
B |
|
С |
равновесия. В случае, показанном на ри- |
|||||||
|
|
|
|
|
|
||||||||||
A |
|
|
|
|
|
сунке, количество опорных реакций по- |
|||||||||
|
|
|
|
|
|
R4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
сле применения аксиомы связей равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 19.1 |
количеству опорных связей, т.е. 4, а не- |
|
зависимых уравнений статики (равнове- |
||
|
сия) в плоской задаче можно составить только 3. Задачи, в которых опорные
реакции или внутренние силовые факторы в конструкции не определяются из одних уравнений статики (равновесия), называются ста-
|
|
A |
|
|
|
|
|
|
|
D |
тически неопределимыми. Задачи расчёта конструкций, в |
|||
P |
|
|
|
|
|
|
|
|
|
|
|
которых уравнений равновесия достаточно для решения |
||
|
B |
|
|
|
|
|
|
|
|
C |
задачи, называются статически определимыми, именно |
|||
|
|
|
|
|
|
|
|
|
такие задачи рассматривались до этого. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стержни и брусья могут использоваться не по одно- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
му, из них могут собираться подчас весьма сложные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стержневые системы. В результате усложнения стержневой |
|
|
Рис. 19.2 |
системы она может стать статически неопределимой, как, |
|||||||||||
P |
|
A |
|
|
|
|
|
|
M1 |
например, рама на рис. 19.2. |
||||
|
|
|
|
|
|
Действительно, опорные реакции для этой рамы лег- |
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
Q2 |
|
|
1 |
|
N1 |
ко определяются. Однако если попытаться определить с |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
помощью метода сечений внутренние силовые факторы в |
M2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
N2 |
сечениях стержня AD, то выясняется, что после рассечения |
|||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
этого стержня конструкция не распадается на две части. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 19.3 |
Приходится рассечь ещё один стержень, например стер- |
|||||||||||
|
|
жень AB (рис. 19.3). После этого конструкция распадается, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и можно записать в плоской задаче три уравнения равновесия одной из её час-
- 30 -
тей. Но неизвестных внутренних усилий, действующих на рассматриваемую часть конструкции, шесть, по три в каждом стержне ( N1, Q1, M1, N2, Q2, M2 ),
так что найти их из одних уравнений равновесия невозможно.
Если из одних уравнений равновесия не удаётся найти внутренние сило- вые факторы, то такая стержневая система называется внутренне статически неопределимой. Если же не удаётся найти опорные реакции, как на рис. 19.1, то конструкция называется внешне статически неопределимой.
Степень статической неопределимости
Степенью статической неопределимости называют разность между числом неизвестных (реакций опор и внутренних силовых факторов) и числом независи-
мых уравнений статики, которые могут быть составлены для их определения. |
|
|||||||
|
|
|
Далее ограничимся рассмотрением плоских задач: s = 4 − 3 =1 для стерж- |
|||||
ня на рис. 19.1; |
s = 6 − 3 = 3 для рамы на рис. 19.2. Тот же результат можно по- |
|||||||
лучить из других соображений. |
|
|
||||||
|
A |
D |
Положение абсолютно твердого тела на плоскости |
|||||
|
определяется тремя |
независимыми координатами или |
||||||
|
|
|
|
|
D* |
|||
P |
|
|
|
степенями свободы. На тело могут быть наложены связи, |
||||
|
|
|
|
|||||
|
B |
|
|
|
C |
т.е. ограничения, обуславливающие его определённое по- |
||
|
|
|
|
ложение на плоскости. Наложение одной простой внеш- |
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
ней связи, которую создаёт шарнирно-подвижная опора, |
||
|
|
|
|
|
|
отнимает одну степень свободы. Если внешних связей |
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
три, то в общем случае абсолютно твердое тело становит- |
||
|
|
Рис. 19.4 |
ся неподвижным на плоскости или, как ещё говорят, ки- |
|||||
|
|
нематически (геометрически) неизменяемым. Кинемати- |
||||||
|
A |
|
|
D |
||||
|
|
|
чески неизменяемой |
является, например, балка |
на |
|||
|
|
|
|
|
|
|||
P |
|
|
|
|
рис. 19.1. |
|
|
|
|
|
|
|
|
|
|||
|
B |
|
|
|
C |
Число связей, при котором достигается кинемати- |
||
|
|
|
|
ческая неизменяемость, называется необходимым числом |
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
связей. Всякая связь, наложенная сверх необходимых, на- |
||
|
|
|
|
|
|
зывается дополнительной. Очевидно, что число дополни- |
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
тельных связей равно степени статической неопредели- |
||
|
|
Рис. 19.5 |
мости стержневой системы. |
|
||||
|
|
Связи в стержневых системах можно разделить |
на |
|||||
|
|
|
|
|
|
|||
внешние и внутренние (взаимные). Внешние связи – это опоры, они накладывают ог- раничения на перемещения всей стержневой системы. Внутренние, или взаимные связи накладывают ограничения на взаимные смещения элементов стержневой сис- темы в направлении степеней свободы стержневой системы.
Рассмотрим пример на рис. 19.4, стержни в точках D и D* не соединены.
