Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

lec9

.pdf

Скачиваний:

Добавлен:

12.03.2015

Размер:

866.32 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

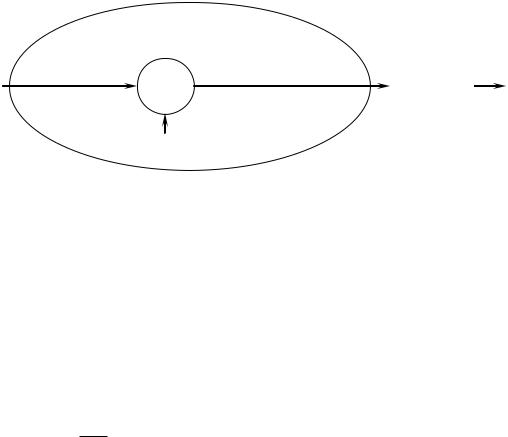
В.Н. Исаков Статистическая теория радиотехнических систем (курс лекций) strts-online.narod.ru

9.Оценивание параметров сигналов

9.1.Постановка задачи оценивания параметра сигнала

Среда, где распространяется сигнал

	s(t, 0 )		ξ (t) s(t, 0 ) n(t)		ˆ
РПдУ	s(t, 0 )	+	ξ (t) s(t, 0 ) n(t)	РПУ	λ
РПдУ		+		РПУ

n(t)

Рис.9.1. К постановке задачи оценивания параметра сигнала

Радиопередающее устройство (РПдУ) на интервале времени [0,Tс ] передаёт детерминированный (квазидетерминированный)

сигнал s(t, ) длительностью Tс с неизвестным значением детерминированного параметра 0 . Распространяясь от РПдУ к

радиоприёмному устройству (РПУ), сигнал подвергается искажающему воздействию аддитивной помехи в виде центрирован-

ного белого гауссова шума n(t) со спектральной плотностью
мощности N ( ) N0 , в результате чего на входе РПУ наблюда-
2
ется реализация процесса
ξ (t) s(t, 0 ) n(t).	(9.1)

Требуется определить правило и соответствующую ему структуру устройства (оценивателя), которое оптимальным образом по результатам обработки реализации ξ (t) процесса ξ (t) позволяет принять решение о том, какое значение принял параметр

9.2. Критерий оптимальности решения задачи оценивания

параметра сигнала

При повторении опытов по оцениванию параметра сигнала, из-за воздействия шума, отклик приёмника будет принимать различные значения, то есть результат оценивания (оценка) является случайной величиной, которая при дискретной обработке процесса ξ (t) зависит от его отсчётов:

В.Н. Исаков Статистическая теория радиотехнических систем (курс лекций) strts-online.narod.ru

λ a(ξ0 , ξ1,..., ξN 1),

(9.2)

где a(x0, x1,..., xN 1) - детерминированная функция N перемен-

ных, которая соответствует правилу (алгоритму, способу) оценивания.

Оптимальной является такая оценка, значения которой, получаемые в различных опытах оказываются локализованными около истинного значения параметра сигнала. Такая оценка обладает свойствами:

1. Несмещённость. То есть математическое ожидание оценки

совпадает с истинным значением параметра сигнала:
mˆ	ˆ		(9.3)
	M λ \|	.
λ

2. Эффективность. То есть среди всех возможных оценок она обеспечивает минимальную дисперсию:

	ˆ
2	D λ \| min .	(9.4)
ˆ	D λ \| min .	(9.4)
λ

9.3. Потенциальная точность оценивания параметра сигнала. Неравенство Крамера-Рао.

Точность оценивания параметра сигнала характеризуется

дисперсией оценки 2 . Покажем, что независимо от способа

оценивания существует нижняя граница для достижимых значений дисперсии оценок. Последующие рассуждения проведём в предположении, что условная ПРВ обрабатываемого процесса wξ (x0 , x1,..., xN 1 | ) , рассматриваемая как функция и называе-

мая функцией правдоподобия, дважды дифференцируема по , а её первая и вторая производные абсолютно интегрируемы.

С учётом свойства математического ожидания (3.25), запи-

шем

m ˆ


	... a(x0 ,..., xN 1)wξ (x0 ,..., xN 1 \| )dx0...dxN 1
			(9.5)
			(9.5)

	a(x)wξ (x \| )dx .

В последнем выражении использована символическая запись многомерных интегралов, используемая для уменьшения

В.Н. Исаков Статистическая теория радиотехнических систем (курс лекций) strts-online.narod.ru

громоздкости математических выражений, в частности обозначе-

но:

x {x0 , x1..., xN 1} - вектор переменных;

dx dx0dx1...dxN 1.

Математическое ожидание оценки также можно предста-

вить в виде:
mˆ ( ) ,	(9.6)
λ

где ( ) - смещение, в общем случае зависит и от параметра сигнала.

С учётом условия нормировки для ПРВ (3.5), приравнивая

(9.5) и (9.6), получим:

a(x)wξ (x | )dx ( ( ))

wξ (x | )dx

				1
Продифференцируем обе части записанного равенства по :

		wξ (x \| )
		wξ (x \| )
	a(x)		dx (1 '( )) wξ (x \| )dx
	a(x)		dx (1 '( )) wξ (x \| )dx


				1

					w (x \| )
				( ( ))	ξ	dx ,
				( ( ))		dx ,

				m ˆ
				m ˆ
				λ

откуда

w (x | )

a(x) m ˆ

dx 1

'( ).

Заметим, что равенство

wξ (x | )

wξ (x | ) wξ (x | )

wξ (x | )

ln wξ (x | )

wξ (x | )

(9.7)

(9.8)

позволяет переписать (9.7) в виде:

a(x) m ˆ

w (x | )

ln w (x | )

f ( x)

g ( x)

В.Н. Исаков Статистическая теория радиотехнических систем (курс лекций) strts-online.narod.ru

1 '( ) 2 . (9.9)

Воспользовавшись неравенством Буняковского – Шварца

	2
		f	2		2		(9.10)
f (x)g(x)dx		f		(x)dx g		(x)dx ,	(9.10)

из последнего выражения получим:

a(x) m ˆ

wξ (x | )dx

ln wξ (x | )

wξ (x | )dx

1 '( ) 2 .

Поскольку (в соответствии с (3.25))

- дисперсия

(a(x) mˆ )

wξ (x | )dx M (λ m ˆ )

| ˆ

оценки при условии, что истинное значение параметра детерминировано, и

	2			2


ln wξ (x \| )		wξ (x \| )dx M	ln wξ (ξ \| )		,

то последнее неравенство можем переписать в виде:

2ˆ

	1 '( ) 2				.
				2
					(9.11)

M		ln wξ (ξ \|	)

(Для краткости в записи математического ожидания условие детерминированности опущено).

Неравенство (9.11) называется неравенством Крамера-Рао. Оно определяет нижнюю границу дисперсии любых оценок. Независимо от структуры оценивателя и способа оценивания невозможно получить дисперсию меньше чем

2ˆ

λ min

	1 '( ) 2				.
				2
					(9.12)

M		ln wξ (ξ \|	)

Нижняя граница дисперсии определяется объёмом выборки и ПРВ обрабатываемого процесса, а также может зависеть от значения параметра .

Рассмотрим другие формы записи (9.12), которые в ряде

В.Н. Исаков Статистическая теория радиотехнических систем (курс лекций) strts-online.narod.ru

случаев оказываются более удобными. Поскольку функция прав-

доподобия wξ (x \| ) удовлетворяет условию нормировки

wξ (x \| )dx 1,

после дифференцирования левой и правой частей, имеем:

wξ

(x | )dx 0

что ввиду (9.8) можно переписать в виде

wξ (x | )

ln wξ (x | )dx 0 .

Дифференцирование последнего выражения по даёт:

wξ (x | )

ln wξ (x | )dx

wξ (x | )

ln wξ (x | )dx 0 .

Первый интеграл в полученном выражении с учётом (9.8)

wξ (x

	\| )
			ln wξ (x
			ln wξ (x

				2

\| )dx	ln wξ (x \|	)			wξ (x \|
\| )dx	ln wξ (x \|	)			wξ (x \|




	M		ln w (ξ
	M		ln w (ξ
					ξ

)dx

	2

\| )		.

Второй интеграл

wξ (x | )

ln wξ (x |

)dx M

ln wξ (ξ | ) .

Таким образом:

ln w (ξ | )

и (9.11) можно также записать в виде:

2ˆ		1 '( ) 2		.
		2
λ min				(9.13)
	M		ln wξ (ξ \| )

	2

Введём в рассмотрение отношение правдоподобия, как отношение ПРВ обрабатываемого процесса, при условии, что пара-

В.Н. Исаков Статистическая теория радиотехнических систем (курс лекций) strts-online.narod.ru

метр сигнала принял значение к ПРВ обрабатываемого процесса, при условии, что сигнал не передавался, то есть на входе оце-

нивателя присутствовал только шум:
	wξ (x \| )
(x \| )		.
	wn (x)

Рассмотрим также логарифм отношения правдоподобия и его производные (в предположении их существования):


	ln (x \| )		ln wξ (x \| );		(9.14а)
	ln (x \| )		ln wξ (x \| );		(9.14а)


	ln (x \| )		ln wξ (x \| );		(9.14б)
	ln (x \| )		ln wξ (x \| );		(9.14б)

2		2
	ln (x \| )			ln wξ (x \| ).	(9.14в)
2	ln (x \| )	2		ln wξ (x \| ).	(9.14в)
2		2

С учётом (9.14в), нижняя граница дисперсии оценок (9.13) может быть представлена в виде:

2ˆ

1 '( ) 2

(9.15)

λ min

ln (ξ | )

В случае непрерывной обработки принимаемого колебания

используется функционал правдоподобия:

2ˆ

1 '( ) 2

(9.16)

λ min

ln [ξ (t) | ]

9.4. Оценка максимального правдоподобия

Согласно

п.9.2

оптимальной

оценкой

ˆ	, ξ1,..., ξN 1) является несмещённая оценка с мини-
λопт aопт (ξ0

мальной дисперсией. (Здесь aопт (x0 , x1,..., xN 1) обозначена опти-

мальная функция оценивания.)				Для такой оценки		смещение
( ) 0, а неравенство Крамера-Рао обращается в равенство
2ˆ	2ˆ			1	.


λопт	λ min		2			(9.17)
		M		ln [ξ (t) \| ]
		M		ln [ξ (t) \| ]
		2

В.Н. Исаков Статистическая теория радиотехнических систем (курс лекций) strts-online.narod.ru

С другой стороны неравенство Крамера-Рао обращается в

равенство, когда обращается в равенство неравенство Буняков-

ского-Шварца (9.10).

Это имеет

место, если

g(x) kf (x) , где

k( ) - произвольная функция, независящая от

x и, в соответст-

вии с (9.9),

f (x) aопт (x) mˆ

wξ (x | ) ,

g(x)

wξ (x | )

ln wξ (x | ),

то есть

ln wξ (x | ) k( ) aопт (x) m ˆ

Так как m ˆ , то

ln wξ (x | ) k( ) aопт (x) .

(9.18)

Полученное равенство выполняется для всех наборов

x , в том

числе и для набора отсчётов реализации обрабатываемого про-

цесса	x	{ 0 , 1,..., N 1}, а также для всех значений парамет-
ра ,	в том числе и для aопт (ξ0,ξ1,...,ξN 1) . В указанном част-

ном случае получим, что значение оптимальной оценки является корнем уравнения

ln wξ (ξ0,ξ1,...,ξN 1 \| )	0.	(9.19)


	aопт (ξ0,ξ1,...,ξN 1)

Полученное уравнение называется уравнением максимального правдоподобия, а полученная оценка – оценкой максимального правдоподобия.

С учётом (9.14б) уравнение максимального правдоподобия можем также записать в виде:


	ln (ξ0,ξ1,...,ξN 1 \| )		0.	(9.20)

		aопт (ξ0,ξ1,...,ξN 1)

Уравнения (9.19)-(9.20) показывают,			что оптимальное оце-

нивание соответствует поиску локального экстремума функций ln wξ (ξ0,ξ1,...,ξN 1 | ) и ln (ξ0,ξ1,...,ξN 1 | ) : оптимальный алгоритм оценивания при каждом фиксированном наборе отсчётов обрабатываемой реализации формирует такое значение оценки

В.Н. Исаков Статистическая теория радиотехнических систем (курс лекций) strts-online.narod.ru

ˆ	которое соответствует значению пара-
λопт aопт (ξ0,ξ1,...,ξN 1) ,
метра сигнала в точке локального экстремума.
В дальнейшем мы	ограничиваемся предположением, что

экстремальная точка m существует, единственна и соответству-

ет глобальному максимуму. Тогда вместо уравнений максимального правдоподобия (9.19)-(9.20), имея в виду также монотонность логарифма, можем рассматривать следующие правила принятия решения

ˆ	(9.21)
aопт (ξ ) : wξ (ξ \| m ) max wξ (ξ \| ) m .	(9.21)

ˆ	(9.22)
aопт (ξ ) : ξ (ξ \| m ) max ξ (ξ \| ) m .	(9.22)

Возвращаясь к определению ПРВ (3.3), выражение (9.21) перепишем в виде:

aопт (ξ ) : P( N 1 i ξ (ti ) i i \| m )
i 0			(9.23)
max P(	N 1	ˆ	(9.23)
max P(		i ξ (ti ) i i \| ) m .
	i 0

Как показывает (9.23), в качестве оценочного принимается такое значение параметра сигнала, для которого наблюдаемая совокупность отсчётов обрабатываемой реализации {0 ,1,...,N 1}

является наиболее вероятной.

При непрерывной обработке принимаемого колебания алгоритм оптимального оценивания определяется функционалом

ˆ aопт [ (t)], а (9.20) и (9.22) преобразуются к виду:


ln [ξ (t) \| ]	0.	(9.24)

	aопт [ξ (t)]

aопт [ξ (t)] : [ξ(t) aопт [ξ(t)] : ln [ξ(t)

| m ] max [ξ (t) | ] ˆ m .

| m ] max ln [ξ (t) | ] ˆ m .

(9.25)

(9.26)

9.5. Структура оптимального оценивателя

Рассмотрим случай, когда параметр сигнала является квантованной величиной {0 , 1,..., M 1}. Оптимальный оценива-

тель, реализующий правило (9.25), должен определить отношение правдоподобия для всех возможных значений параметра сиг-

В.Н. Исаков Статистическая теория радиотехнических систем (курс лекций) strts-online.narod.ru

нала, и то значение, для которого отношение правдоподобия максимально, предложить в качестве оценки, чему соответствует следующее правило принятия решения:

aопт [ξ(t)] : [ξ(t) \| m ]	ˆ	(9.27)
aопт [ξ(t)] : [ξ(t) \| m ]	max [ξ(t) \| i ] m .	(9.27)
	i 0...M 1

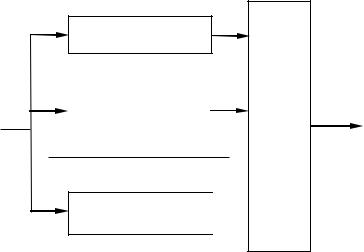
Полученному правилу соответствует схема, показанная на рис.9.1. Оцениватель является многоканальным устройством.

[ (t) | 0 ]

(t)		СВМ	ˆ
	[ (t) \| 1]

[ (t) | M 1]

Рис.9.1. Структурная схема оптимального оценивателя

Каждый канал содержит блок, в котором определяется функционал отношения правдоподобия от принимаемой реализации при соответствующем значении параметра сигнала. Схема выбора максимума (СВМ) определяет канал с максимальным откликом, соответственно которому и формируется значение оценки.

Схема, соответствующая (9.26) аналогична показанной на рис.9.1, с той разницей, что в каждом канале оценивателя формируется значение логарифма функционала отношения правдоподобия.

При уменьшении шага квантования параметра полученные в п.9.5 результаты приближаются к случаю непрерывного изменения параметра.

При использовании многоканальных оценивателей для оценки непрерывного параметра, шаг квантования для формирования значений параметра, соответствующих различным каналам, можно выбирать, руководствуясь средним квадратическим от-

клонением оценки λˆ . Чрезмерное уменьшение шага квантования приведёт лишь к более точному представлению ошибок

В.Н. Исаков Статистическая теория радиотехнических систем (курс лекций) strts-online.narod.ru

оценивания.

9.6. Оценивание параметров детерминированного сигнала 9.6.1. Оценивание амплитуды детерминированного сигнала

Оцениваемым параметром сигнала является	амплитуда
A. Выражение для сигнала запишем в виде:
s(t, A) As0 (t) ,	(9.28)

где s0 (t) - детерминированный сигнал с энергией E0 . Отношение правдоподобия в рассматриваемом случае даётся (7.27):

где

R s

[

E s2 (t, A)dt

Tc (t)s(t, A)dt

			E		2R
(t) \| A] exp				exp	s	,
(t) \| A] exp				exp		,
			N0		N0
			N0		N0
Tc
	A2s02 (t)dt	A2E0 ;
0

Tc (t) As0 (t)dt AR s0 .

Логарифм отношения правдоподобия

ln [ (t) \| A]	2AR s0	A2 E0	,	(9.29)

	N0	N0

Рассматривая (9.29) как функцию A нетрудно установить, что мы имеем дело с многочленом второй степени. График указанной функции представляет собой параболу, ветви которой направлены в сторону отрицательных ординат. Эта функция имеет единственный локальный максимум, который является и глобальным.

Функционал оптимального оценивания определим, используя уравнение максимального правдоподобия (9.24). Для этого найдём производную (9.29):

		2AR s		A2E		2R s		2AE
			0		0		0		0
A ln [ξ (t) \| A]	A	N	0	N	0	N	0	N	0	;
			0		0		0		0

запишем уравнение максимального правдоподобия:

2R s0	2AE0		2R s0	2aопт [ξ (t)]E0	0 ;
N0	N0		N0	N0
		A aопт [ξ (t)]

найдём его решение:

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.20151.05 Mб24lec5.pdf
#
12.03.2015864.18 Кб29lec6.pdf
#
21.08.2019134.14 Кб2Lec6f.doc
#
12.03.2015941.86 Кб29lec7.pdf
#
12.03.2015843.65 Кб22lec8.pdf
#
12.03.2015866.32 Кб16lec9.pdf
#
28.09.2019217.09 Кб2lect2.doc
#
18.08.2019216.06 Кб6Lection 2.doc
#
18.08.2019341.5 Кб4Lection 3.doc
#
18.08.2019195.58 Кб4Lection 5.doc
#
18.08.2019239.1 Кб2Lection 6.doc


	ln (x \| )		ln wξ (x \| );		(9.14а)
	ln (x \| )		ln wξ (x \| );		(9.14а)


	ln (x \| )		ln wξ (x \| );		(9.14б)
	ln (x \| )		ln wξ (x \| );		(9.14б)

2		2
	ln (x \| )			ln wξ (x \| ).	(9.14в)
2	ln (x \| )	2		ln wξ (x \| ).	(9.14в)
2		2