5.3. Алгебраические критерии устойчивости.

Алгебраические критерии устойчивости позволяют судить об устойчивости системы по коэффициентам характеристического уравнения , являющегося знаменателем передаточной функции.

Рассмотрим следующие алгебраические критерии: критерий Вышнеградского, критерий Гурвица и критерий Рауса.

5.3.1. Критерий Вышнеградского

- Критерий Вышнеградского применяется для исследования систем автоматического регулирования 3-го порядка с характеристическим уравнением

(59)

Уравнение (59) приводится к нормализованному виду:

(60)

Для подстановки в уравнение (60) вводится переменная .

После преобразований выражение (60) приобретает вид .

Переменные Х и У выражаются через коэффициенты исходного уравнения. Условием устойчивости является неравенство ХУ >1. При ХУ = 1 система находится на колебательной границе устойчивости. Линия ХУ = 1, изображенная на рисунке 52, отображает границу устойчивости на плоскости ХУ и называется гиперболой Вышнеградского.

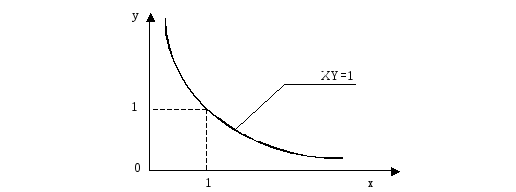
Рис. 52. Гипербола Вышнеградского

5.3.2. Критерий Гурвица

Критерий Гурвица применяется для определения устойчивости системы по значениям коэффициентов характеристического уравнения.

Применение данного критерия требует построения главного определителя Гурвица и вычисления определителей Гурвица. Главный определитель Гурвица имеет n-й порядок, где n - степень характеристического уравнения.

По главной диагонали определителя записывают в порядке возрастания индексов коэффициенты от а₁ до а_n. Вверх от главной диагонали столбцы заполняют коэффициентами с последовательно возрастающими индексами, вниз заполняют коэффициентами с последовательно убывающими индексами. Вместо отсутствующих коэффициентов ставят нули. В последнем столбце остается одно ненулевое значение а_n.

Определители младшего порядка получают как диагональные миноры определителя ,

и т.д.

Критерий Гурвица требует, чтобы все определители Гурвица были больше 0 (при условии, что а₀ больше нуля). Если хотя бы один определитель меньше 0, система неустойчива.

Система находится на колебательной границе устойчивости при совместном соблюдении следующих условий:

1) 2)

3) 4)

Апериодическая граница устойчивости требует соблюдения следующих условий:

1) 2)

3) 4)

5.3.3. Критерий Рауса

Для определения устойчивости САУ по критерию Рауса требуется построить таблицу Рауса и исследовать знаки элементов ее первого столбца. Построение таблицы Рауса показано в таблице 3. В первой строке таблицы ставят коэффициенты с четными, а во второй – с нечетными последовательно возрастающими индексами. Элементы третьей и последующих строк находятся с использованием вспомогательных коэффициентов через элементы следующего столбца двух предыдущих строк. Вспомогательные коэффициенты определяются как отношение элементов первого столбца двух предыдущих строк.

Таблица 3. Таблица Рауса.

Вспомогательный коэффициент	Столбец№ № строки				...
–					...
–					...
				...	...
...	...	...	...	...	...
…

В последней (n+1) строке остается только один ненулевой элемент. Система устойчива, если все элементы 1-го столбца таблицы Рауса больше 0 при условии, что . Если хотя бы один элемент первого столбца меньше нуля, то система неустойчива. Система находится на апериодической границе устойчивости, еслии на колебательной границе устойчивости, если предпоследний элемент первого столбца равен 0, остальные положительны. Данный критерий имеет преимущественное применение для системы высокого порядка, так как сложность вычислений с увеличением порядка не повышается.