8. Факторный анализ

Таблицы для кластерного анализа приведены в Приложении 1.

Факторный анализ, как правило, используется для сокращения количества исходных факторов и упрощения за счёт этого математической модели моделируемой системы. Факторный анализ – раздел многомерного статистического анализа, объединяющий методы оценки размерности множества наблюдаемых переменных посредством исследования структуры ковариационных или корреляционных матриц. Основное предположение факторного анализа заключается в том, что корреляционные связи между большим числом наблюдаемых переменных факторов определяется существованием меньшего числа гипотетических ненаблюдаемых переменных или факторов. Общей моделью факторного анализа служит следующая линейная математическая зависимость:

(2)

где F_j– общие факторы,

U_i– характерные факторы,

e_i– случайные ошибки,

Количество общих факторов R<Vрекомендуется выбирать так, чтобы они объясняли не менее 90% изменчивости, вносимой исходными факторами задано, случайные величиныe_iнезависимы между собой и с величинамиF_jиU_i. Постоянные коэффициентыa_ij– называются факторными нагрузками (нагрузкаi–той переменной наj–й фактор). Значенияa_ij,b_i, считаются неизвестными параметрами, подлежащими оценке.

Главными целями факторного анализа являются: сокращение числа переменных (редукция данных) и определение структуры взаимосвязей между переменными, т.е. классификация переменных. Поэтому факторный анализ используется или как метод сокращения данных, или как метод классификации.

Для проведения факторного анализа предлагается технология, включающая в себя следующие этапы:

1. Сбор исходных данных и подготовка корреляционной (ковариационной) матрицы.

2. Выделение первоначальных (ортогональных) факторов.

3. Вращение факторной структуры и содержательная интерпретация результатов факторного анализа.

Выделение первоначальных факторов – это, прежде всего, выбор метода факторного анализа. Наиболее используемыми методами являются:

1. Метод главных компонент, в котором поиск решения идёт в направлении вычисления собственных векторов (факторов), а собственные значения характеризуют дисперсию (разброс) по факторам.

2. Метод главных факторов, под которым понимают применение метода главных компонент к редуцированной корреляционной матрице. Редуцированной корреляционной матрицей называют матрицу парных коэффициентов корреляции, в которой на главной диагонали вместо единиц указаны значения оценок общностей.

Основное различие двух моделей факторного анализа состоит в том, что в анализе главных компонент предполагается, что должна быть использована вся изменчивость переменных, тогда как в анализе главных факторов используется только изменчивость переменной, общая и для других переменных. В большинстве случаев эти два метода приводят к весьма близким результатам. Однако метод анализа главных компонент часто более предпочтителен как метод сокращения данных, в то время как метод анализа главных факторов лучше применять с целью определения структуры данных.

Вращение факторной структуры – это “поворот” факторов в пространстве для достижения простой структуры, в которой каждая переменная характеризуется преобладающим влиянием какого-то одного фактора.

Выделяется два класса вращения: ортогональное и косоугольное. К ортогональным методам относится метод “Варимакс” (Kaiser, 1958), максимизирующий дисперсию факторных нагрузок по каждому фактору в отдельности, что приводит к увеличению больших нагрузок и к уменьшению маленьких.

При интерпретации факторов можно начать работу с выделения наибольших факторных нагрузок исходных факторов в конкретном общем факторе. Для выделения можно использовать приёмы, аналогичные выделению значимых коэффициентов корреляции, то есть оценивать факторные нагрузки, сравнивая их по величине с критическими значениями коэффициентов корреляции. Для подбора названий общих факторов нет формализованных приёмов, и для этого можно довериться интуиции.

В РГР количество исходных факторов сравнительно невелико и поэтому факторный анализ требуется провести по совокупностям откликов, выделив по ним общие отклики и классифицировать их.

Результатыфакторногоанализа:

Numberofvariables: 16

Method: Principal components

log(10) determinant of correlation matrix: -15,455

Number of factors extracted: 2

Eigenvalues: 8,34129 2,38667

Графические результаты факторного анализа:

Рис.27

Численные нагрузки факторов:

Рис.28

Объяснимая дисперсия (собственные значения):

Рис.29

Общности:

Рис.30

Воспроизведенная корреляционная матрица:

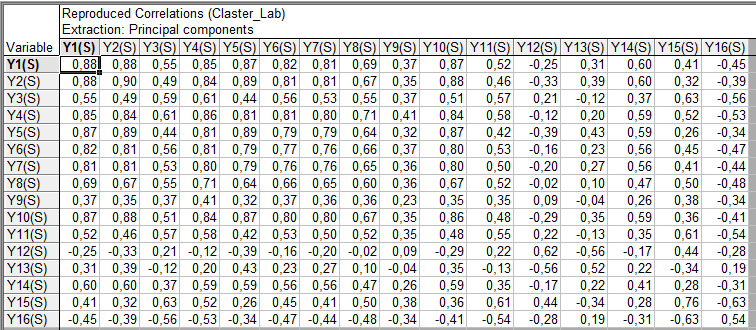
Рис.31

Остаточная корреляционная матрица:

Рис.32

График собственных значений, где по оси ординат отложены номера собственных значений, по оси абсцисс – соответствующие численные значения:

Рис.33