Министерство образования Российской Федерации

Ивановский государственный энергетический университет

Кафедра менеджмента и маркетинга

Математические методы и модели в управлении

Методические указания для самостоятельной работы студентов заочной формы обучения

Иваново 2003

Составитель И.Г. ШЕЛЕПИНА

Редактор Ю.Ф. БИТЕРЯКОВ

Методические указания предназначены для студентов факультета экономики и управления заочной формы обучения и бакалавриата, изучающих курсы «Математические методы и модели в управлении» и «Математические методы и модели в экономике».

В методических указаниях представлено содержание курса, список рекомендуемой литературы, задания для контрольной работы и краткие указания по ее выполнению.

Утверждены цикловой методической комиссией ФЭУ.

Рецензент

Кафедра экономики и организации предприятия Ивановского государственного энергетического университета

Содержание курса

Тема 1. Основные вопросы применения математических методов в экономике и управлении.

Основные понятия и этапы экономико-математического моделирования. Классификация экономико-математических методов и моделей.

Тема 2. Оптимизационные методы и модели в управлении экономическими системами.

2.1. Линейное программирование.

Принцип оптимальности в планировании и управлении, общая задача оптимального программирования. Формы записи задачи линейного программирования и ее экономическая интерпретация. Геометрическая интерпретация задачи (геометрический метод решения задачи). Симплексный метод решения задач линейного программирования (с естественным и искусственным базисом). Теория двойственности в анализе оптимальных решений экономических задач.

2.2. Транспортная задача линейного программирования (закрытая). Метод потенциалов.

Тема 3. Вероятностно-статистичесике методы моделирования экономических систем.

Теория массового обслуживания. Классификация систем массового обслуживания. Количественные характеристики. Показатели эффективности систем массового обслуживания.

Тема 3. Балансовый метод.

Экономико-математическая модель межотраслевого баланса. Коэффициенты прямых и полных материальных затрат.

Далее в данных методических указаниях представлены варианты контрольной работы и краткие указания по ее выполнению.

Контрольная работа выполняется студентами индивидуально на основе лекционного материала. Номер варианта контрольной работы - это последняя цифра номера зачетной книжки (цифре 0 соответствует 10 вариант).

Задания для контрольной работы вариант №1

Задача 1.

Решить графическим методом следующую задачу линейного программирования: ,

_{, ,}

_{, .}

Задача 2.

Предприятие располагает 3-мя видами сырья и может выпускать одну и ту же продукцию двумя способами. При этом за 1 час работы первым способом выпускается 20 единиц продукции, а вторым способом - 30 единиц продукции. Количество сырья (кг) того или иного вида, расходуемого за 1 час при различных способах производства, и запасы сырья (кг) приведены в таблице.

Тип сырья	Способ производства		Запас сырья, кг.
	1сп.	2сп.
С1	10	20	100
С2	20	10	100
С3	15	15	90

Сформулировать экономико-математическую модель задачи и, используя симплексный метод решения задач линейного программирования, найти такое время (час) использования первого и второго способов производства, при котором будет выпущено наибольшее количество продукции.

Задача 3.

Решить следующую транспортную задачу:

А=(100; 150; 50), В=(75;80;60;85), 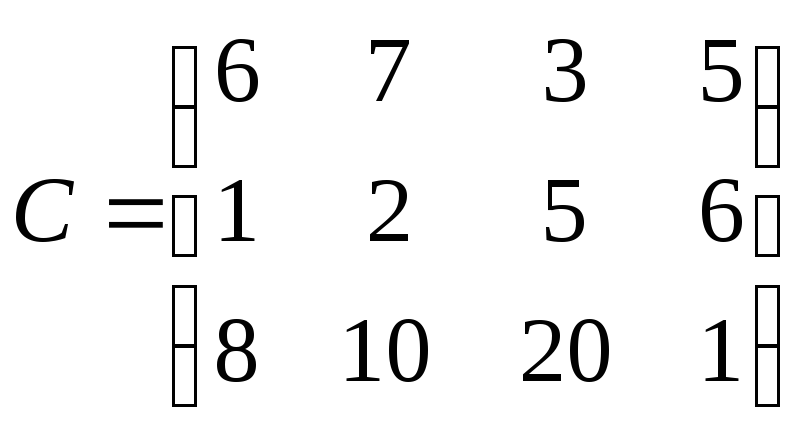, где А - вектор мощностей поставщиков, В – вектор мощностей потребителей, С – матрица транспортных издержек на единицу груза.

Задача 4.

На АЗС имеются 2 колонки для заправки автомоби­лей. Автомобили подъезжают на АЗС в соответствии с пуассоновским распределением со средней частотой 2 авто­мобиля за 5 мин. Заправка автомобиля в среднем длится 3 мин, и продолжительность заправки распределена по экс­поненциальному закону. Требуется определить:

а) вероятность того, что у АЗС не окажется ни одного ав­томобиля;

б) вероятность того, что обе колонки будут заняты;

в) среднюю длину очереди в ожидании заправки;

г) среднее время ожидания автомобиля в очереди.

Задача 5.

На основании данных, приведенных в таблице, рассчитать коэффициенты прямых и полных материальных затрат.

Отрасль	Прямые межотраслевые потоки		Конечная продукция
	1	2
1	50	80	70
2	25	50	50