Пример 2-8 Проецирование в однородных координатах

Для отрезка АВ из рис. 2-14 имеем р = q = 1, [А] = [1 3 1] и [В] = [4 1 1],

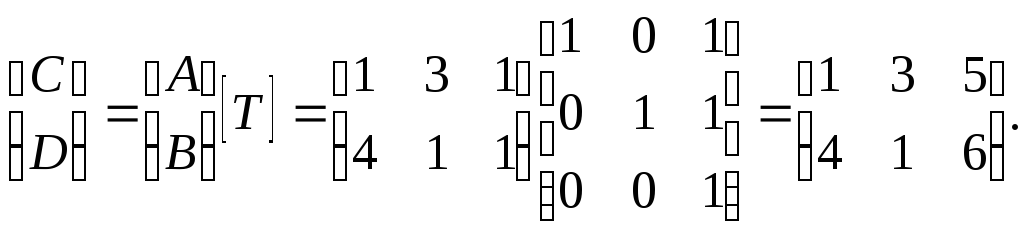
Таким образом, [С] = [1 3 5] и [D] = [4 1 6] на плоскости h=x+y+1. Проецируя обратно на плоскость h = 1 путем деления на коэффициент однородных координат, проведем двумерное преобразование точек

Результат показан на рис. 2-14.

19. ПРОПОРЦИОНАЛЬНОЕ МАСШТАБИРОВАНИЕ

Оставшийся необъясненным элемент s (3 х 3)-матрицы преобразования соответствует пропорциональному масштабированию, при котором все компоненты вектора изменяются пропорционально. Покажем это, рассмотрев следующее преобразование:

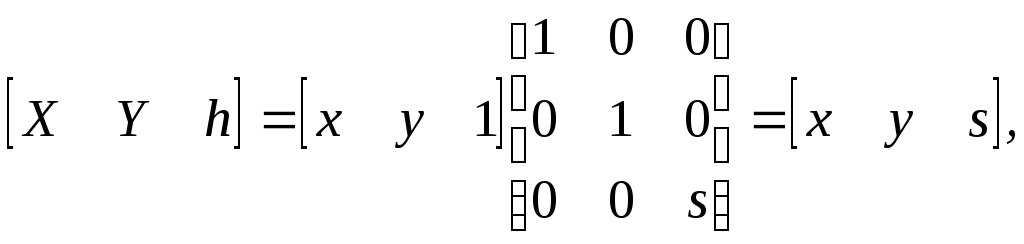(2-58)

г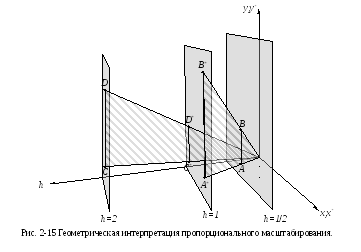деX = x, Y = y и h = s. После нормализации получим X = x/s и Y = у/s. Таким образом, преобразование [х у 1][Т] = [x/s y/s l] является равномерным масштабированием координатного вектора. Если s < 1, то происходит растяжение, а если s > 1 —сжатие.

Заметим, что это преобразование осуществляется также в плоскости h = 1. Здесь h = s = const, и поэтому плоскость h1 параллельна плоскости h = 1. Геометрическая интерпретация данного эффекта показана на рис. 2-15. Если s<1, то h = const задает плоскость, лежащую между плоскостями h = 1 и h = 0. Следовательно, когда преобразуемая прямая АВ проецируется обратно на плоскость h = 1, то АВ увеличивается. Аналогично, если s > 1, то h = const определяет плоскость, расположенную за плоскостью h = 1 и проходящую вдоль оси h. В случае проецирования прямой CD на плоскость h = 1 происходит уменьшение прямой CD.

20. ТОЧКИ БЕСКОНЕЧНОСТИ

Однородные координаты предоставляют удобный и эффективный способ нанесения точек из одной системы координат в соответствующие точки альтернативной координатной системы. Бесконечная область в одной координатной системе часто преобразуется в конечную область в альтернативной системе. При некорректном выборе переноса параллельность прямых может не сохраняться. Однако точки пересечения после преобразования оказываются снова в точках пересечения. Данное свойство используется для определения однородных координат представления точек бесконечности.

Рассмотрим пару пересекающихся прямых, заданных уравнениями

.

Прямые пересекаются в точке с координатами х = 3/5, у = 2/5. Запишем уравнения в виде x+y - 1 = 0, 2х – 3y = 0 и представим их в матричной форме

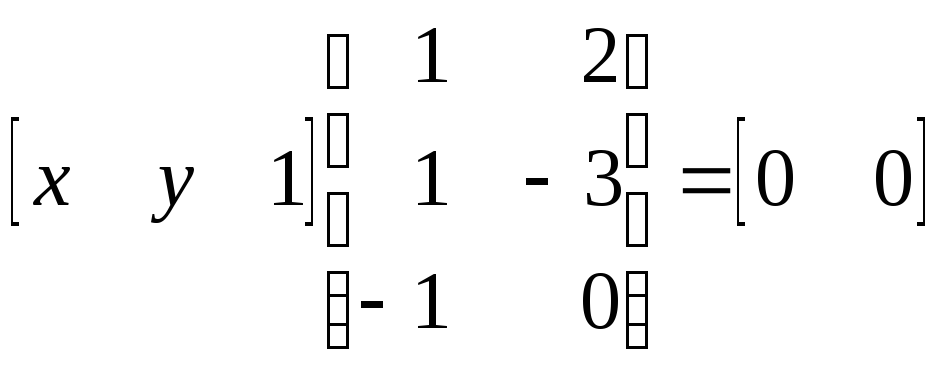
или

Если матрица [M'] квадратная, то пересечение может быть получено путем обращения матрицы. Изменим систему исходных уравнений следующим образом:

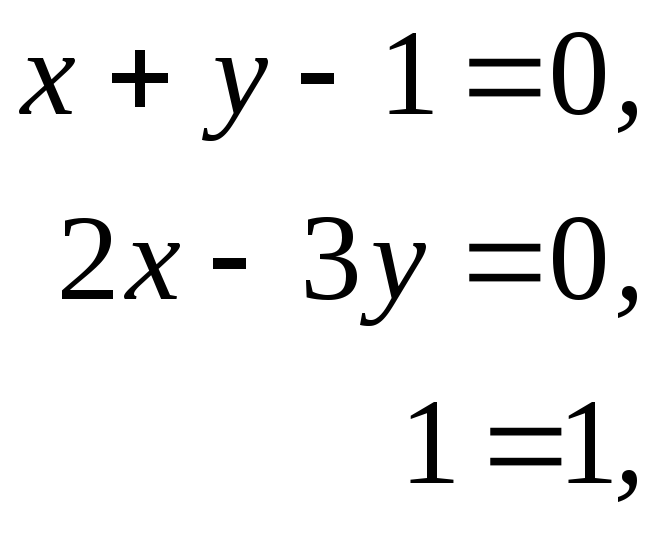
или в матричной форме

т.е.

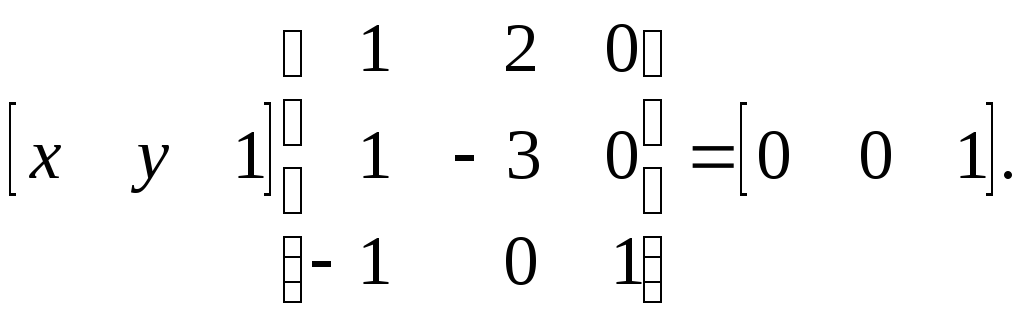
Квадратная матрица, обратная данной, имеет следующий вид:

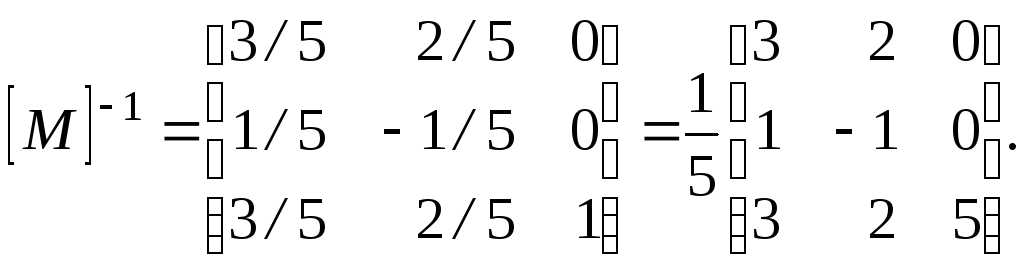
Умножая обе части уравнения на [М]^-1 и учитывая, что [М][М]^-1 = [I] является тождественной матрицей, получим

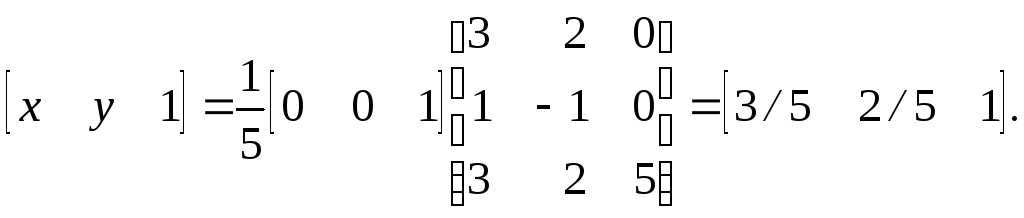
Таким образом, точка пересечения опять имеет координаты х = 3/5, у = 2/5.

Рассмотрим теперь две параллельные прямые, заданные следующим образом

По определению геометрии Евклида, точка пересечения двух параллельных прямых расположена в бесконечности. Продолжая предыдущие рассуждения, вычислим точку пересечения этих прямых, заданных в матричной форме,

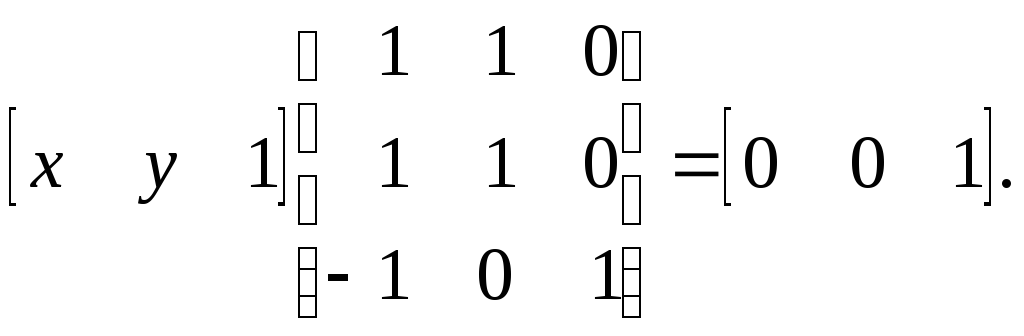
Однако несмотря на то что матрица квадратная, она не имеет обратной, так как две ее строки тождественны. Такая матрица называется сингулярной. Возможна иная формулировка с обратимой матрицей. Получим ее, переписывая систему уравнений следующим образом:

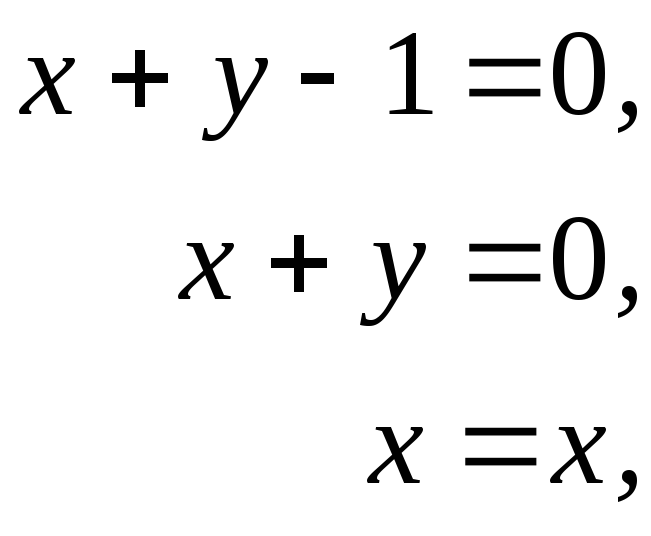
или в матричной форме

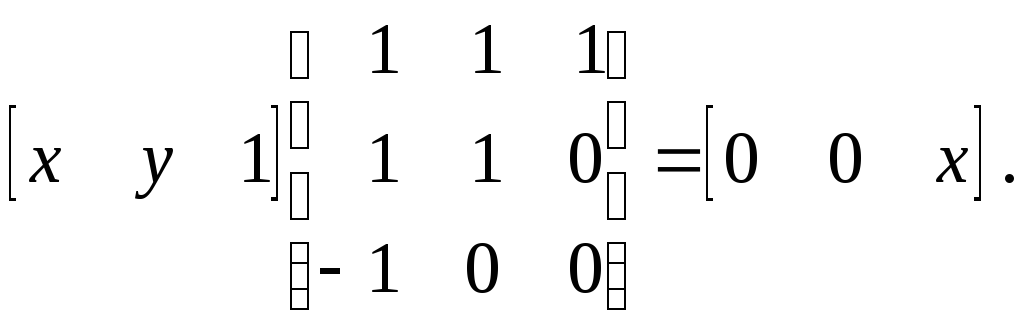
В данном случае матрица не является сингулярной и существует обратная ей

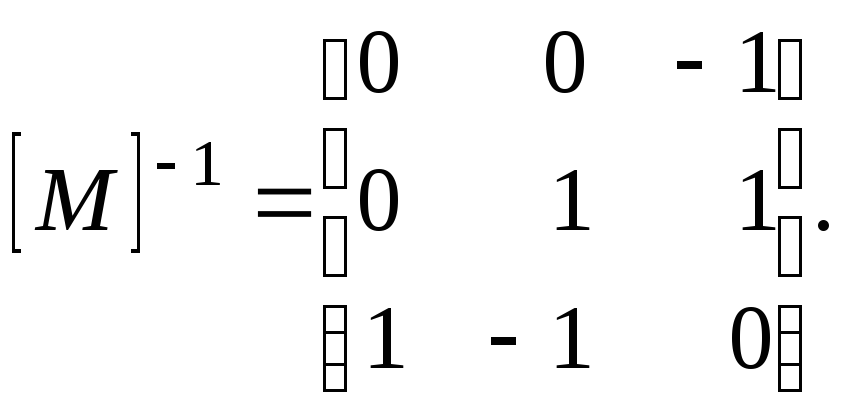
Умножая обе части выражения на обратную матрицу, получаем

.

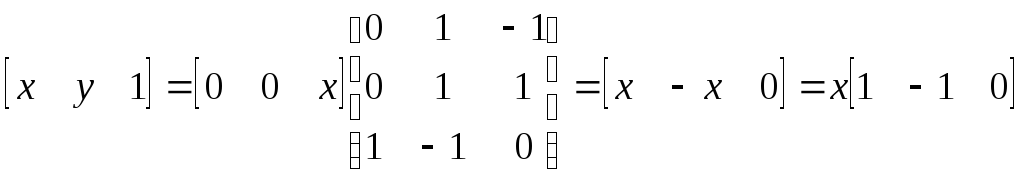Результирующие однородные координаты [1 -1 0] определяют точку пересечения двух параллельных прямых, т.е. точку бесконечности. В частности, они представляют данную точку в направлении [1 -1] двумерного пространства. В общем виде двумерный координатный вектор [а b 0] представляет точку бесконечности на прямой ау - bх = 0. Приведем несколько примеров:

[ 1 0 0] точка на положительной оси x,

[-1 0 0] точка на отрицательной оси х,

[ 0 1 0] точка на положительной оси у,

[ 0 -1 0] точка на отрицательной оси у,

[ 1 1 0] вдоль прямой у = х в направлении [1 1].

Таблица 2-1 Однородные

координаты для точки [4 3]

h x* y* X Y