Пример 2-3 Отражение и вращение

Рассмотрим треугольник ABC, показанный на рис. 2-7. Первоначально

отобразим его относительно оси х (уравнение 2-33), а затем относительно прямой у=-х (см. выражение (2-36)). Результатом первого отображения будет

.

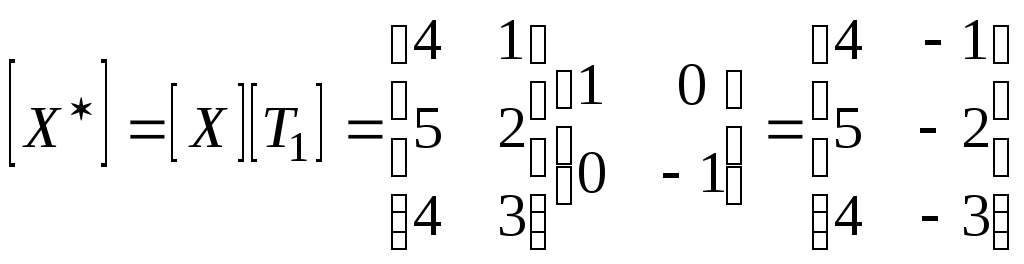Результатом второго будет

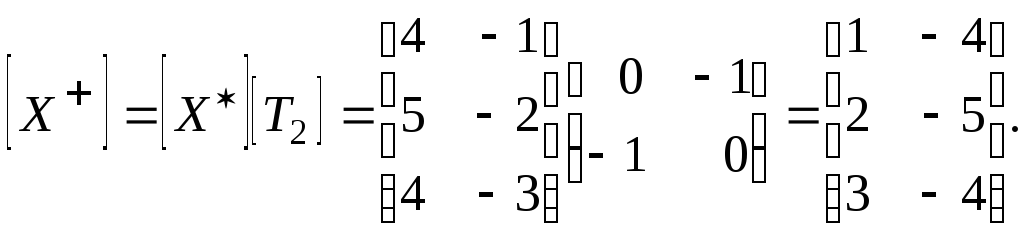
Повернем треугольник относительно начала координат на угол  = 270° (см. (2-29)) и получим аналогичный результат

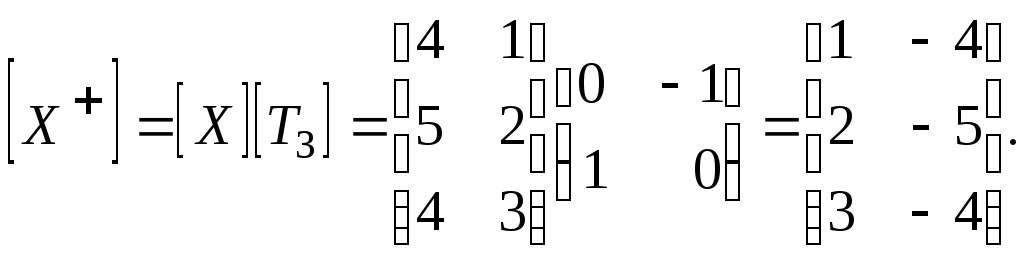
Отметим, что матрицы отражения из (2-33) и (2-36) ортогональны, т. е. транспонированная матрица одновременно является обратной. Например,

.

11. МАСШТАБИРОВАНИЕ

Из наших рассуждений относительно преобразования точек следует, что величина масштабирования определяется значением элементов исходной диагональной матрицы. Если матрица

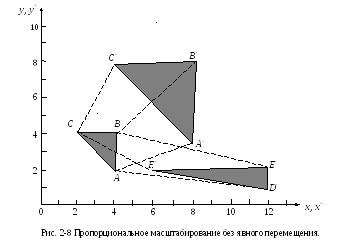
используется в качестве оператора воздействия на вершины треугольника, то имеет место «двукратное» расширение или равномерное масштабирование относительно точки начала координат. Если значения элементов не равны, то треугольник искажается, что проиллюстрировано на рис. 2-8. Треугольник ABC, преобразованный с помощью последней матрицы переходит в пропорционально увеличенный треугольник АВС. Тот же треугольник, но преобразованный с помощью матрицы

переходит в треугольник DEF, имеющий искажение, вызванное разными коэффициентами масштабирования.

В общем случае при матрице

(2-37)

в которой а = d, b = с = 0, выполняется пропорциональное масштабирование; если то масштабирование будет проведено непропорционально. В первом случае дляа = d > 1 происходит расширение, т. е. увеличение изображения. Если а = d < 1, то происходит равномерное сжатие, т.е. фигура уменьшается. Непропорциональное расширение и сжатие возникают в зависимости от значений a и d, которые могут быть меньше либо больше, чем 1, независимо друг от друга.

Из рис. 2-8 видно также, что на первый взгляд преобразование треугольника является перемещением. Это объясняется тем, что относительно начала координат масштабируются координатные векторы, а не точки.

Для того чтобы лучше понять этот факт, рассмотрим преобразования ABC в DEF более внимательно. В частности,

Заметим, что каждая из компонент х координатных векторов треугольника ABC умножалась на масштабный коэффициент 3, а компоненты у делилась на 2.

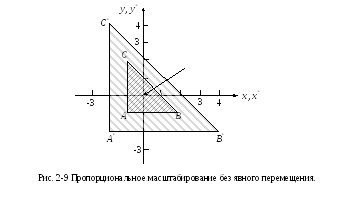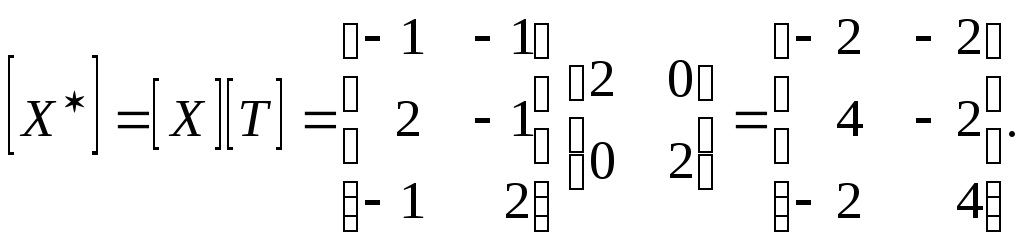
Для того чтобы получить чистое масштабирование без эффекта перемещения, центр фигуры надо поместить в начало координат. Это видно из рис. 2-9, на котором треугольникABC увеличивается в два раза при масштабировании относительно его центра с координатами, равными 1/3 основания и 1/3 высоты. Конкретная матрица преобразования имеет вид

12. КОМБИНИРОВАННЫЕ ПРЕОБРАЗОВАНИЯ

Возможности матричного метода достаточно ясно описаны в предыдущих разделах. С помощью матричных операций над координатными векторами, определяющими вершины фигур, можно управлять формой и положением поверхности. Однако для получения желаемой ориентации может потребоваться более одного преобразования. Так как операция умножения матриц не коммутативна, то важен порядок выполнения преобразования.

Для иллюстрации эффекта некоммутативности операции умножения матриц рассмотрим преобразования поворота и отражения координатного вектора [х у]. Если вслед за поворотом на 90° (посредством [T₁]) производится отражение относительно прямой у = -x (посредством [T₂]), то эти два последовательных преобразования дают

и затем

С другой стороны, если отражение следует за поворотом, то получатся следующие результаты:

и

Оба результата различны, что подтверждает важность порядка применения матричных преобразований.

Другое принципиальное обстоятельство иллюстрируется этими результатами и приведенным ниже примером. Ранее отдельные матричные преобразования применялись последовательно к результатам предыдущих преобразований, например

и

В приведенном ниже примере отдельные преобразования предварительно комбинируются или конкатенируются, а затем полученная матрица применяется к исходному вектору, т.е. [T₁][T₂] [T₃] и [х у] [Т₃] [x у].