Пример 2-6 Поворот относительно произвольной точки

Предположим, что центр объекта лежит в точке [4 3]. Требуется повернуть объект на прямой угол против часовой стрелки вокруг центра. Используя матрицу

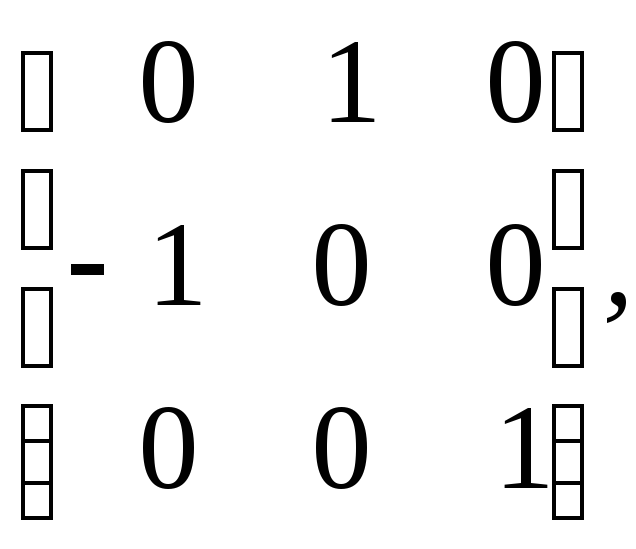
проведем поворот вокруг начала координат, не совпадающего с центром объекта. Обязательной процедурой преобразования является, прежде всего, такое перемещение объекта, чтобы желаемый центр вращения оказался в начале координат. Это достигается с помощью следующей матрицы перемещения:

Далее применяем матрицу поворота и, наконец с помощью матрицы перемещения приведем результаты поворота обратно к первоначальному центру. Вся операция

может быть реализована одной матрицей путем простого перемножения отдельных матриц, т.е.

.

17. ОТРАЖЕНИЕ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ПРЯМОЙ

Ранее в разделе 2-10 обсуждалось отражение относительно прямых, проходящих через начало координат. Иногда требуется выполнить отражение объекта относительно прямой, не проходящей через точку начала координат. Это можно сделать, воспользовавшись процедурой, аналогичной вращению вокруг произвольной точки. Конкретно выполняются следующие действия:

• перемещение линии и объекта таким образом, чтобы линия прошла через начало координат;

• поворот линии и объекта вокруг точки начала координат до совпадения с одной из координатных осей;

• отражение относительно координатной оси;

• обратный поворот вокруг начала координат;

• перемещение в исходное положение.

В матричном виде данное преобразование имеет представление

(2-53)

где — матрица перемещения, R — матрица поворота вокруг начала координат, — матрица отражения.

Перемещения, повороты и отражения также применяются для преобразования произвольных фигур. Рассмотрим следующий пример.

Пример 2-7 Отражение относительно произвольной прямой

Рассмотрим прямую L и треугольник ABC (рис. 2-13а). Уравнение прямой L имеет вид .

Координатные векторы [2 4 1], [4 6 1] и [2 6 1] задают вершины треугольника ABC.

Прямая L пройдет через начало координат при перемещении ее на -2 единицы в направлении оси у. В результате этого при повороте вокруг начала координат на - tg^-1(l/2) = -26.57° прямая совпадет с осью х. Выражение (2-33) используется для отражения треугольника относительно оси х, затем преобразованные координатные векторы треугольника поворачиваются и перемещаются к исходной ориентации. Комбинация преобразований будет иметь вид

и конкретно для координатных векторов треугольникаАВС имеем

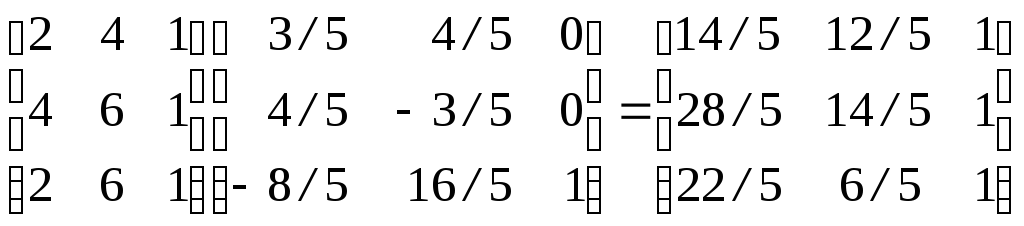
(рис. 2-13a). Рис. 2-13 b, c, d, e иллюстрируют различные этапы данного преобразования.

18. ПРОЕЦИРОВАНИЕ-ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ОДНОРОДНЫХ КООРДИНАТ

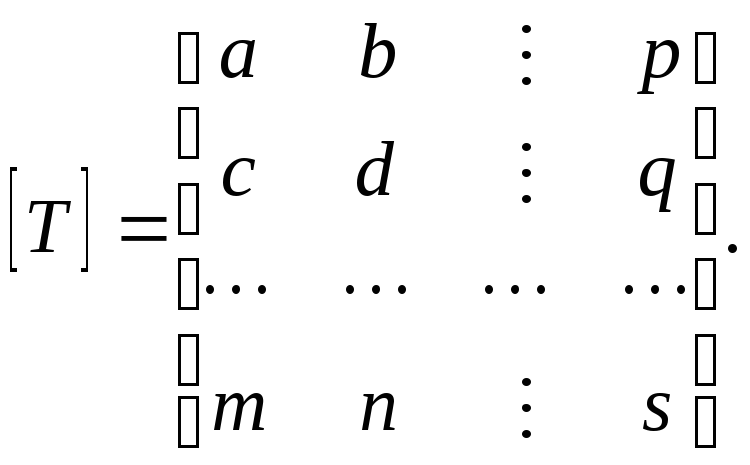
Матрицу преобразования размером 3x3 для двумерных однородных координат можно разбить на четыре части

(2-54)

Напомним, что а, b, c и d — коэффициенты масштабирования, вращения, отражения и сдвига соответственно. Элементы т и п задают перемещение. В двух предыдущих разделах коэффициенты имели значения p = q = 0 и s = 1. Установим величины р и q не равными 0. Какой эффект мы получим? В данном случае полезно рассмотреть геометрическую интерпретацию.

При p = q = 0 и s = 1 однородные координаты преобразованных векторов всегда равны h = 1. Геометрически данный результат интерпретируется как ограничение преобразования физической плоскостью h = 1.

Для иллюстрации эффекта преобразования при p и q отличных от нуля, рассмотрим следующее выражение:

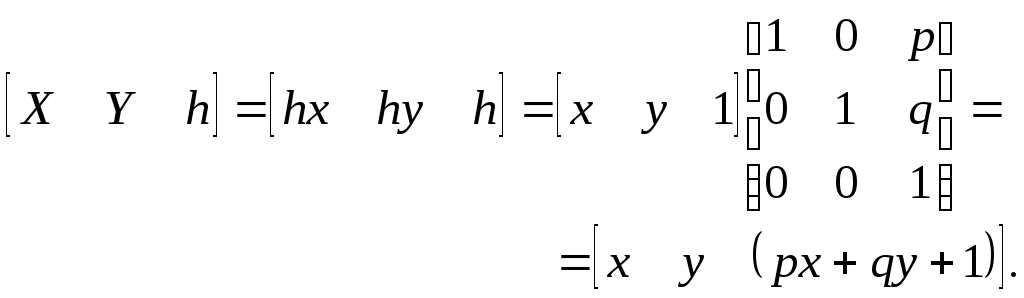(2-55)

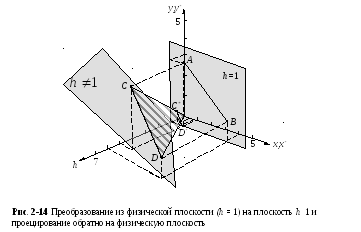
Здесь X = hx, Y = hy и h = рх + qy +1. Преобразованный координатный вектор, выраженный в однородных координатах, лежит теперь в трехмерном пространстве, определенном как h = px + qy + 1. Это преобразование показано на рис. 2-14, где отрезок АВ, принадлежащий физической плоскости h = 1, преобразуется в CD со значением h 1, т. е. рХ + qY - h + 1 = 0.

Однако представляют интерес результаты, принадлежащие физической плоскости с h = 1, которые можно получить путем геометрического проецирования прямой CD с плоскости h 1 обратно на плоскость h = 1 с использованием для этого проецирующих лучей, проходящих через начало координат. Из рис. 2-14, используя правило подобия треугольников, получим

или в однородных координатах

После этого, нормализуя выражение (2-55) делением однородных координат на величину h, получаем

(2-56)

или

(2-57a)

(2-57b)

Детально действие преобразования рассмотрим на следующем примере.