
- •Обзор машинной графики
- •Двумерные преобразования
- •Пример 2-1 Средняя точка прямой
- •Пример 2-2 Пересекающиеся прямые
- •Пример 2-3 Отражение и вращение
- •Пример 2-4 Комбинированные преобразования на плоскости
- •Пример 2-5 Масштабирование области
- •Пример 2-6 Поворот относительно произвольной точки
- •Пример 2-7 Отражение относительно произвольной прямой
- •Пример 2-8 Проецирование в однородных координатах
- •1 4 3 4 3
- •Трехмерные преобразования
- •Пример 3-1 Комбинированное преобразование
Пример 2-2 Пересекающиеся прямые
Рассмотрим две штриховые линии АВ и EF на рис. 2-3, конечные точки которых имеют координаты
![]()
и
![]() .
.
![]() Уравнение
прямой АВ
имеет вид
-(2/3) х +
у = -1/3, а прямая EF
задается
уравнением х
+ у = 1. В
матричном виде пучок прямых представляется
в виде
Уравнение
прямой АВ
имеет вид
-(2/3) х +
у = -1/3, а прямая EF
задается
уравнением х
+ у = 1. В
матричном виде пучок прямых представляется
в виде
![]()
Используя матрицу обратного преобразования (2-21), получим точку пересечения этих прямых
![]()
Теперь преобразуем эти линии с помощью матрицы
![]()
Результирующие
прямые А![]() В
В![]() и E
и E![]() F
F![]() показаны на
рис. 2-3. В матричном виде уравнения
преобразованных линий имеют вид
показаны на
рис. 2-3. В матричном виде уравнения
преобразованных линий имеют вид
![]()
с
точкой пересечения
![]() .
.
Преобразуя точку пересечения исходных линий, получим
![]()
что тождественно точке пересечения преобразованных линий.
Из рис. 2-3 и примера
2-2 видно, что исходные штриховые прямые
АВ и
EF
не
перпендикулярны
друг другу. Однако преобразованные
прямые А![]() В
В![]() и E
и E![]() F
F![]() ,
показанные
сплошной линией, являются перпендикулярными.
Таким образом, преобразование [T]
переводит две пересекающиеся
неперпендикулярные прямые в две
пересекающиеся перпендикулярные. Смысл
обратного преобразования [T]-1
состоит в
переводе двух пересекающихся
перпендикулярных прямых в две
пересекающиеся, но не перпендикулярные,
что может привести к неприятным
геометрическим последствиям. Значительный
интерес представляет вопрос, при каком
условии перпендикулярные прямые
преобразуются в перпендикулярные. Мы
вернемся к этому вопросу в разд. 2-14, где
разберем его подробнее.
,
показанные
сплошной линией, являются перпендикулярными.
Таким образом, преобразование [T]
переводит две пересекающиеся
неперпендикулярные прямые в две
пересекающиеся перпендикулярные. Смысл
обратного преобразования [T]-1
состоит в
переводе двух пересекающихся
перпендикулярных прямых в две
пересекающиеся, но не перпендикулярные,
что может привести к неприятным
геометрическим последствиям. Значительный
интерес представляет вопрос, при каком
условии перпендикулярные прямые
преобразуются в перпендикулярные. Мы
вернемся к этому вопросу в разд. 2-14, где
разберем его подробнее.
Дополнительное изучение рис. 2-3 и примера 2-2 показывает, что преобразование [Т] включает в себя поворот, отражение и масштабирование. Рассмотрим каждое из этих преобразований отдельно.
ПОВОРОТ
Рассмотрим треугольник ABC (рис. 2-4) и с помощью следующего преобразования повернем его на 90° против часовой стрелки относительно начала координат
![]() .
.
Если использовать матрицу размером (3 х 2), состоящую из координат х и у вершин треугольника, то можно записать
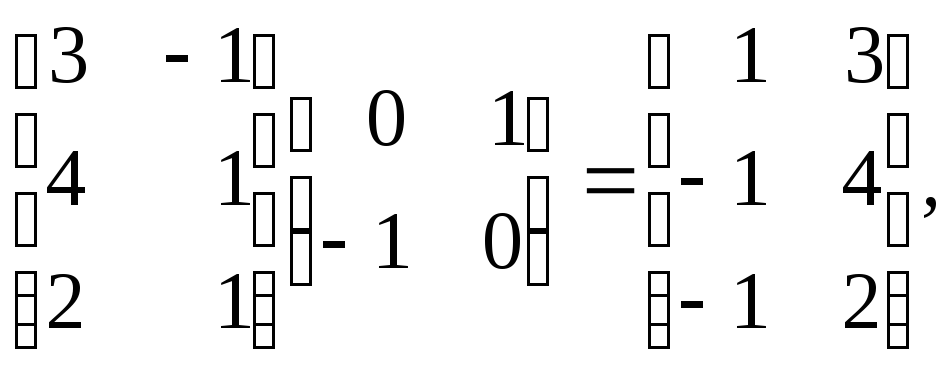
что является
координатами результирующего треугольника
А![]() В
В![]() С
С![]() .
.
Поворот на 180° относительно начала координат достигается путем следующего преобразования
![]() ,
,
а на 270о относительно начала координат преобразованием
![]() .
.
Разумеется, что матрица тождественного преобразования
![]()
соответствует повороту вокруг начала координат на 0° или 360°. Обратим внимание, что в этих примерах не встречаются ни масштабирование, ни отражение.
В
этих примерах осуществляется преобразование
в специальных случаях поворота
вокруг начала координат на углы 0°, 90°,
180° и 270°. Как осуществить поворот
вокруг точки начала координат на
произвольный угол
? Для ответа на
этот вопрос рассмотрим вектор положения
от начала координат до точки Р
(рис.
2-5). Обозначим r
—длину вектора, а
![]() —угол
между вектором и осью х.
Вектор
положения поворачивается вокруг начала
координат на угол
и
попадает в
точку Р
—угол
между вектором и осью х.
Вектор
положения поворачивается вокруг начала
координат на угол
и
попадает в
точку Р![]() .
Записав
векторы положений для Р
и Р
.
Записав
векторы положений для Р
и Р![]() .
получаем:
.
получаем:
![]()
и
![]()
![]() .
.
Используя формулу
для cos
суммы углов, перепишем выражение для
Р![]() следующим
образом
следующим
образом
![]()
Сравнивая три последних выражения, получим
![]() (2-27a)
(2-27a)
![]() (2-27b)
(2-27b)
или в матричном виде

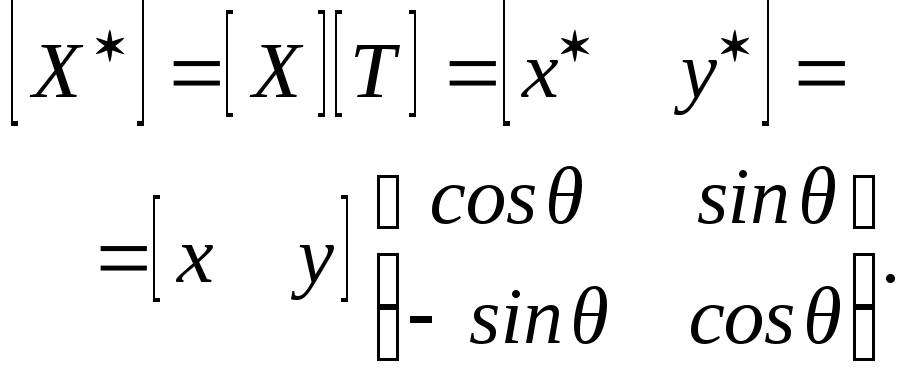 (2-28)
(2-28)
 Итак,
преобразование поворота вокруг точки
начала координат на произвольный угол
задается
матрицей
Итак,
преобразование поворота вокруг точки
начала координат на произвольный угол
задается
матрицей
![]() (2-29)
(2-29)
Повороты являются положительными, если они осуществляются против часовой стрелки относительно точки вращения (рис. 2-5).
Определитель общей матрицы поворота имеет следующий вид:
![]() (2-30)
(2-30)
В общем случае преобразования по матрице с детерминантом, равным 1, приводят к полному повороту.
Предположим теперь,
что требуется возвратить точку Р![]() обратно в
Р,
т. е. выполнить обратное преобразование.
Очевидно, что требуемый угол поворота
равен -.
Из формулы (2-29) возьмем матрицу для
выполнения необходимого преобразования
обратно в
Р,
т. е. выполнить обратное преобразование.
Очевидно, что требуемый угол поворота
равен -.
Из формулы (2-29) возьмем матрицу для
выполнения необходимого преобразования
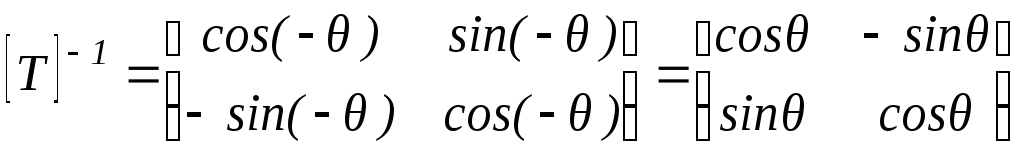 ,
(2-31)
,
(2-31)
так как cos(-) = cos и sin(- ) = - sin. Выражение [T]-1 является формальной записью обратной матрицы [T]. Можно показать, что матрица [Т]-1 является обратной к [T], если вспомнить, что результат умножения матрицы на обратную дает единичную матрицу. В нашем случае:
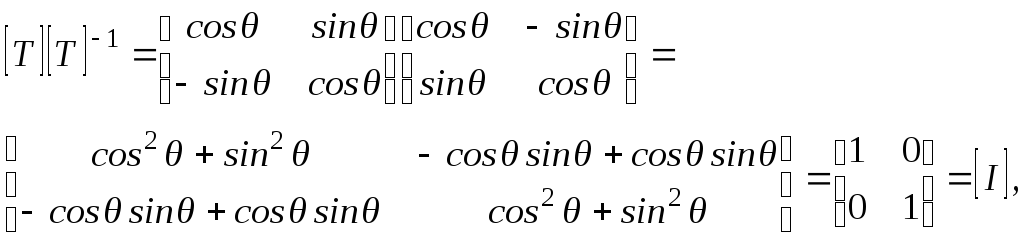
где [I] —единичная матрица.
Анализ выражений (2-29) и (2-31) приводит к другому интересному и полезному результату. Вспомним, что транспонирование матрицы определяется заменой ее строк столбцами. Обозначим транспонированную матрицу [Т] как [Т]T. Сравнивая ее с [T]-1, видим, что
![]() (2-32)
(2-32)
Обратная матрица вращения является транспонированной. Поскольку формально определитель обратной матрицы вычисляется гораздо сложнее, чем определитель транспонированной, то выражение (2-32) является достаточно важным и полезным результатом. В общем случае обратной для любой матрицы преобразования полного поворота, т. е. матрицы с определителем, равным +1, является ее транспонированная матрица (такие матрицы называют ортогональными).
ОТРАЖЕНИЕ
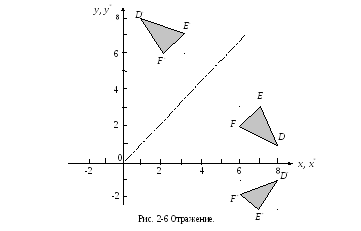
В то время как полный поворот на плоскости ху обычно осуществляется в двумерном пространстве относительно нормали к плоскости, отражение представляет собой тот же поворот на угол 180° в трехмерном пространстве и обратно на плоскость относительно оси, лежащей в плоскости ху. На рис. 2-6 приведены примеры двух отражений на плоскости треугольника DEF. Отражение относительно прямой у = 0 (ось х) получено с использованием матрицы
![]() .
(2-33)
.
(2-33)
В этом случае новые
вершины треугольника D![]() E
E![]() F
F![]() будут
определяться преобразованием
будут
определяться преобразованием
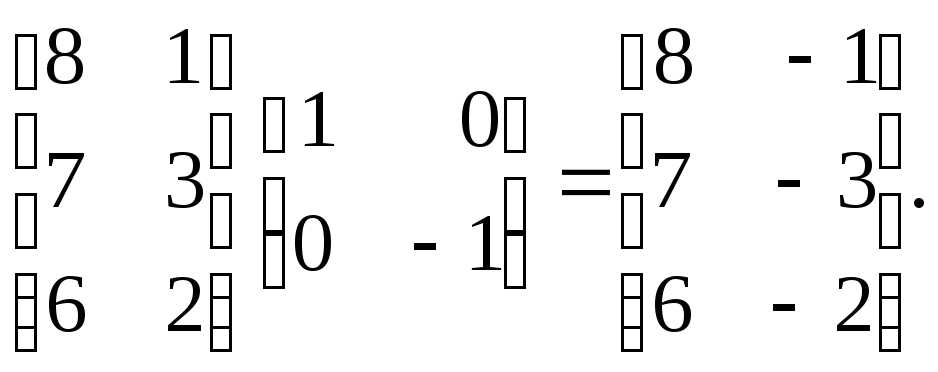
Подобным образом отражение относительно оси у при х = 0 будет иметь вид
![]() (2-34)
(2-34)
Отражение относительно прямой у = х осуществляется с помощью матрицы
![]() .
(2-35)
.
(2-35)
Выполнив преобразования, получим координаты вершин треугольника D+E+F+
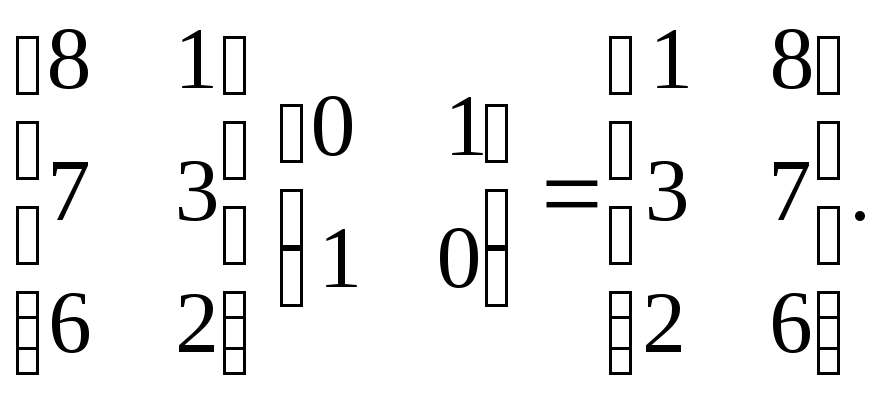
Аналогичным образом отражение относительно оси х будет иметь вид
![]() (2-36)
(2-36)
У каждой из этих матриц определитель равен -1. В общем случае, если определитель матрицы преобразования равен -1, то преобразование дает полное отражение.
Если оба полных отражения осуществляются последовательно относительно прямых, проходящих через начало координат, то результатом будет полный поворот относительно начала координат. Это можно увидеть, обратившись к следующему примеру.
