Пример 2-1 Средняя точка прямой

Рассмотрим отрезок AB из рис. 2-2. Положение векторов конечных точек такое: [А] = [0 1], [В] = [2 3]. Преобразование [Т] =осуществляет перемещение вектора на линиюАВ:

Средняя точка A^*B^* будет иметь координаты

Координаты средней точки линии AB равны

Преобразуем среднюю точку и получим

что полностью эквивалентно предыдущему результату.

Применением этих результатов в машинной графике любая прямая может быть преобразована в любую другую прямую путем простого преобразования ее конечных точек и восстановления линии между ними.

7. ПРЕОБРАЗОВАНИЕ ПАРАЛЛЕЛЬНЫХ ЛИНИЙ

Результатом преобразования двух параллельных линий с помощью (2x2)-матрицы снова будут две параллельные линии. Это можно увидеть, рассмотрев линию между точками [А] = [x₁ y₁], [В] = [x₂ y₂] и параллельную ей линию, проходящую между точками Е и F. Покажем, что для этих линий любое преобразование сохраняет параллельность. Так как АВ, EF и АВ и ЕF параллельны, то угол наклона линий АВ и EF определяется следующим образом:

(2-16)

Преобразуем конечные точки АВ, воспользовавшись матрицей общего преобразования размером (2 х 2):

(2-17)

Наклон прямой АВ определяется следующим образом:

или

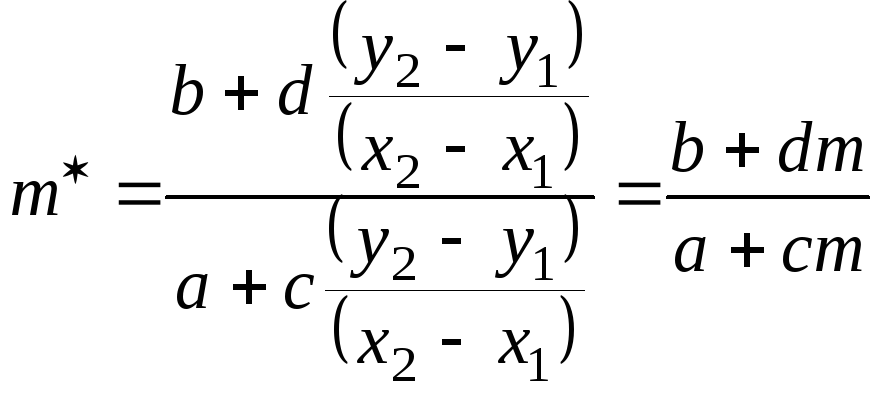. (2-18)

Так как наклон т не зависит от x₁, x₂, y₁, y₂ , а m, a, b, c и d одинаковы для EF и АВ, то т одинаково для ЕF и АВ. Таким образом, параллельные линии сохраняют параллельность и после преобразования. Это означает, что при преобразовании (2 х 2) параллелограмм преобразуется в другой параллелограмм. Эти тривиальные выводы демонстрируют большие возможности использования матрицы преобразования для создания графических эффектов.

8. ПРЕОБРАЗОВАНИЕ ПЕРЕСЕКАЮЩИХСЯ ПРЯМЫХ

Результатом преобразования с помощью (2 х 2)-матрицы пары пересекающихся прямых линий также будет пара пересекающихся линий. Проиллюстрируем этот факт на примере двух прямых, изображенных на рис. 2-3 штриховой линией и заданных уравнениями

В матричном представлении эти уравнения будут иметь вид:

или [X][M]=[B]. (2-19)

Если существует решение этой системы уравнений, то линии пересекаются, в противном случае они параллельны. Решение можно найти путем инверсии матрицы.

В частности,

(2-20)

Матрица, обратная [M], имеет следующий вид:

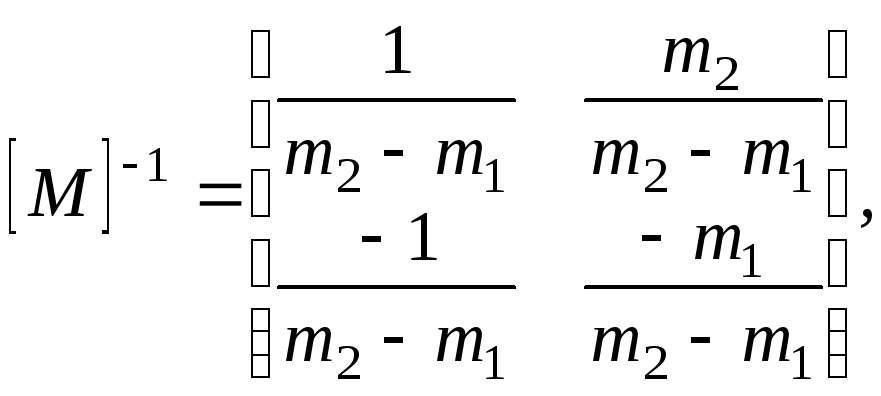(2-21)

так как [М][М]^-1= [I], где [I] —единичная матрица. Поэтому координаты точки пересечения двух линий можно найти следующим образом:

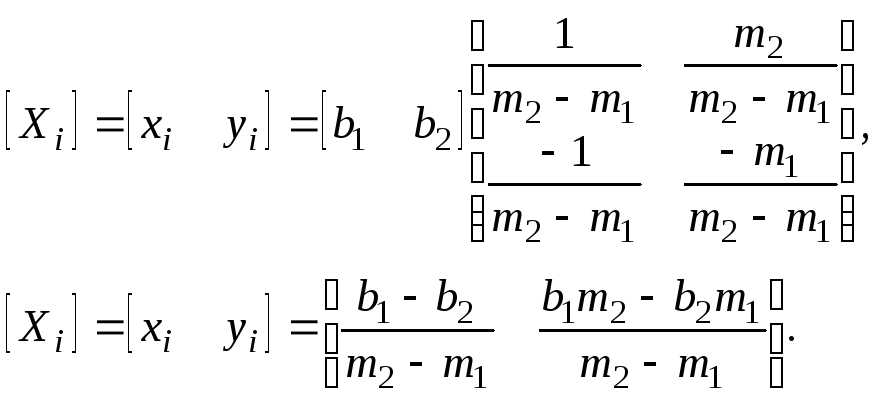(2-22)

Если обе линии преобразовать с помощью (2 х 2)-матрицы общего преобразования вида

,

то их уравнения будут иметь вид

Соответственно можно показать, что

(2-23)

и гдеi=1,2 (2-24)

Точка пересечения линий после преобразования отыскивается таким же образом, как и в случае исходных линий:

.

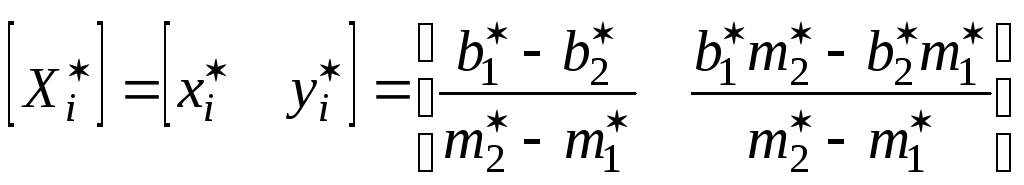Воспользовавшись выражениями (2-23) и (2-24), получим

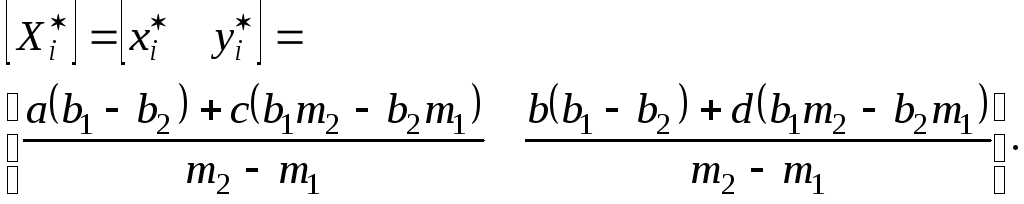(2-25)

Возвращаясь теперь к точке пересечения [x_i y_i] исходных линий и применяя уже полученную матрицу преобразования, имеем

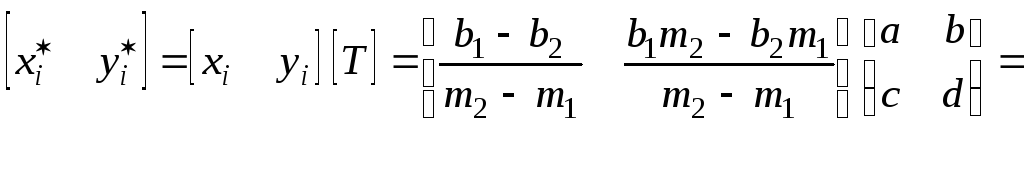
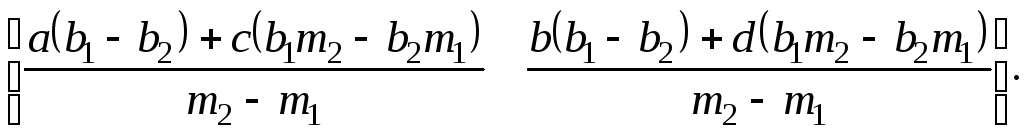(2-26)

Сравнение уравнений (2-25) и (2-26) показывает, что они одинаковы. Итак, точка пересечения преобразуется точно в другую точку пересечения.