3. Трехмерные преобразования

   1. ВВЕДЕНИЕ

В трехмерном пространстве также можно ввести однородные координаты так, что точке будет соответствовать бесконечное множество точекчетырехмерного пространства, гдеh-любое ненулевое число. Мы рассмотрим некоторые элементарные преобразования в трехмерном пространстве и выпишем соответствующие им матрицы преобразований.

2. ПОВОРОТЫ ВОКРУГ ОСЕЙ

В отличие от двумерного случая в трехмерном имеется три основных поворота – вокруг оси X, вокруг оси Y и вокруг оси Z. Вращение пространства вокруг оси Z на угол против часовой стрелки (если смотреть с конца вектораZ) соответствует повороту в плоскости XY. При этом координата z не меняется, поэтому матрица такого вращения имеет вид

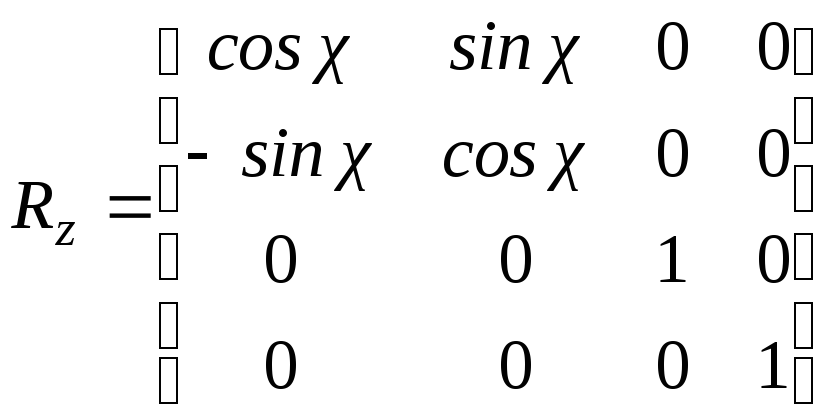. (3-1)

Вращение против часовой стрелки вокруг оси X на угол соответствует повороту в плоскостиYZ. То есть это вращение полностью аналогично предыдущему с точностью до переименования осей . Поэтому, переставляя соответствующим образом (а именно,) строки и столбцы матрицы (3-1), получим матрицу:

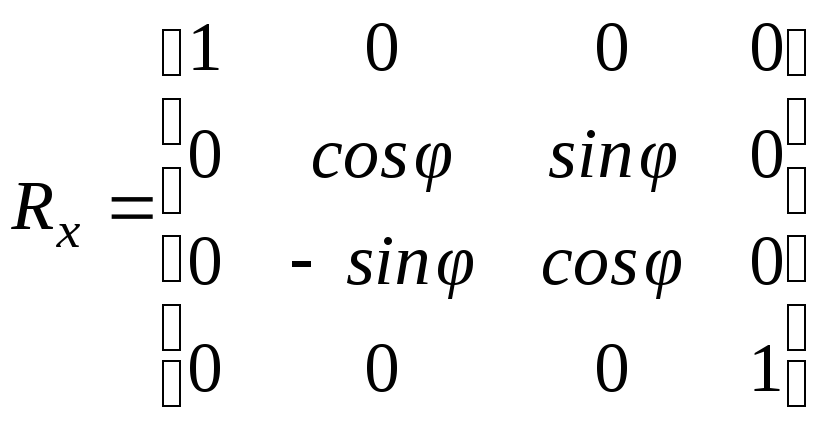. (3-2)

Аналогично, матрица поворота вокруг оси Y на угол  против часовой стрелки получается из матрицы (3-1) следующей перестановкой строк и столбцов: . В результате получаем матрицу

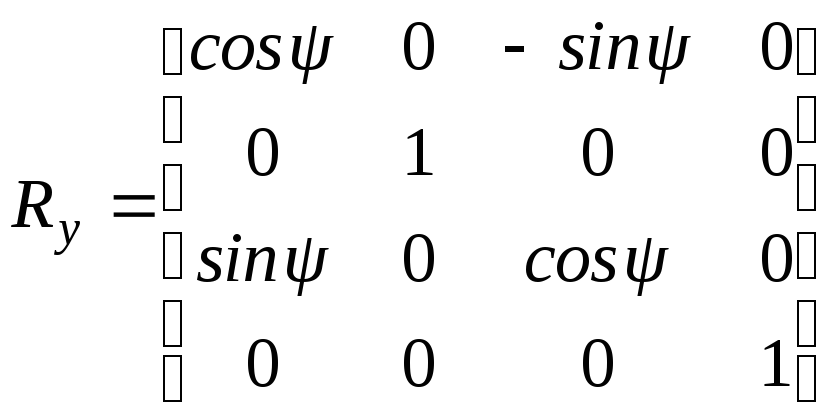. (3-3)

3. РАСТЯЖЕНИЕ ВДОЛЬ ОСЕЙ

Растяжение (сжатие) вдоль осей X, Y, Z с коэффициентами соответственно a, b, c > 0 осуществляется с помощью матрицы следующего вида

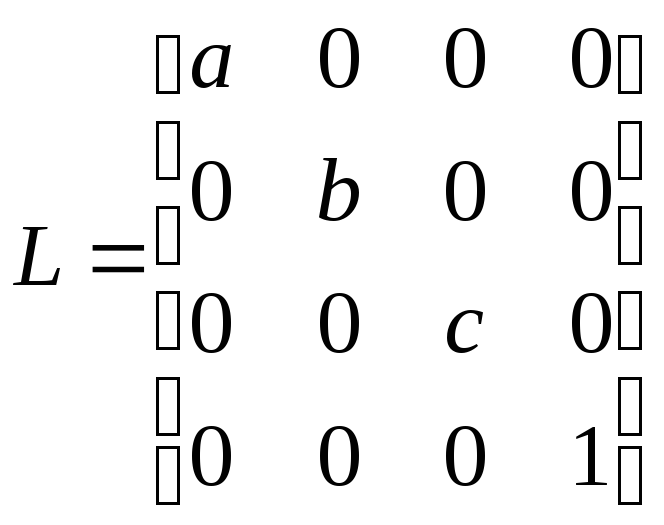. (3-4)

4. ОТРАЖЕНИЕ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ

При отражении, например, относительно плоскости XY координаты x и y не изменяются, а координата z меняет знак. Аналогичная ситуация при отражении относительно других плоскостей: YZ и ZX. Поэтому соответствующие матрицы будут иметь вид:

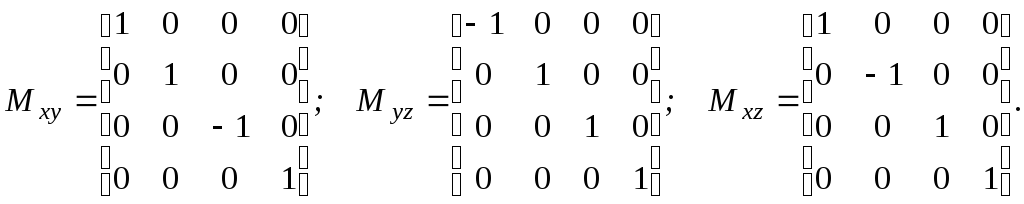
5. Перенос (сдвиг)

Матрица переноса (сдвига) пространства на вектор d = (d₁, d₂, d₃) имеет вид

. (3-5)

Пример 3-1 Комбинированное преобразование

Рассмотрим пример более сложного преобразования, которое мы представим в виде последовательности элементарных преобразований. Пусть требуется построить матрицу M вращения пространства на угол вокруг прямойL, проходящей через точку A(a,b,c) и имеющей единичный направляющий вектор (l,n,0), то есть параллельный плоскости XY (рис. 3-1).

Задача сводится к последовательному применению следующих элементарных преобразований:

• сделаем так, чтобы прямая L проходила через начало координат. Для этого надо осуществить перенос пространства на вектор –A=(-a, -b, -c). Соответствующая матрица преобразования имеет вид:

.

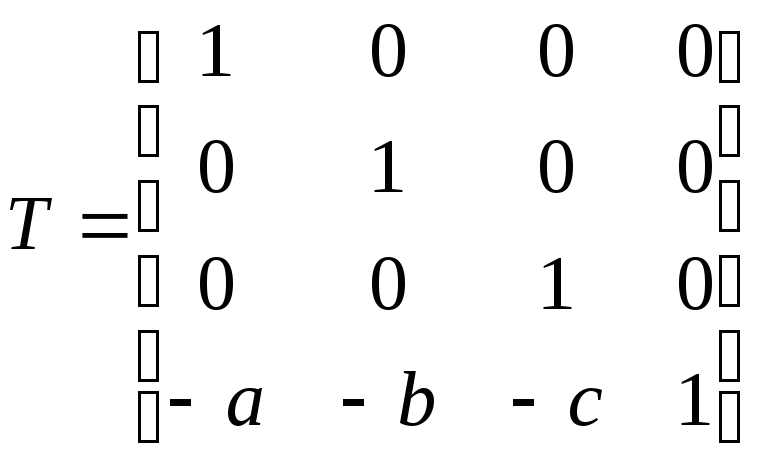
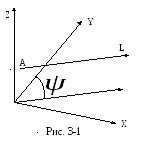• совместим прямую L с осью Y. Для этого выполним поворот пространства на угол 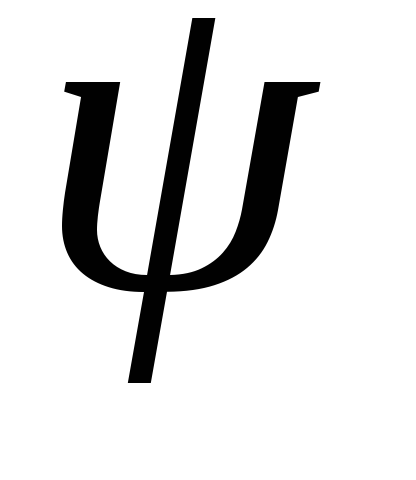(который надо еще вычислить) вокруг осиZ. Зная направляющий вектор (l, n, 0) прямой L, получаем для угла :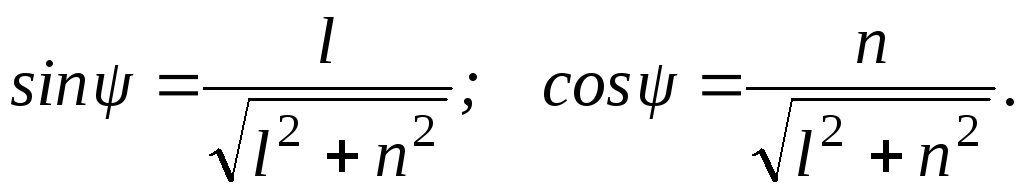Соответствующая матрица имеет вид:

.

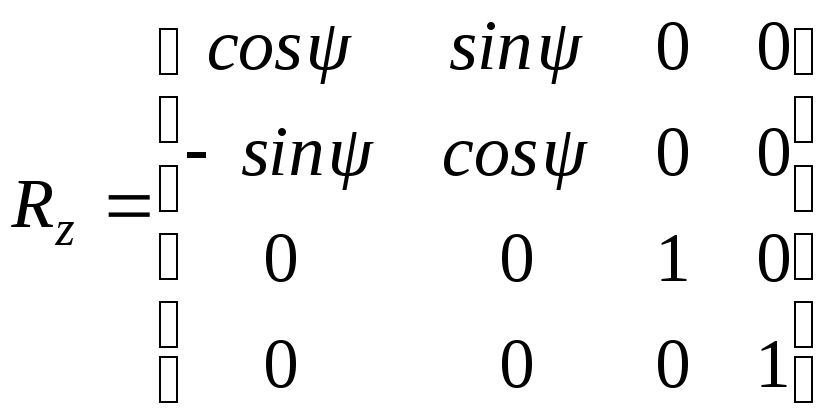• повернем пространство на угол вокруг прямойL. Так как теперь прямая L совпадает с осью Y, то это будет поворот вокруг оси Y и соответствующая матрица (см. 3-3) будет следующей:

.

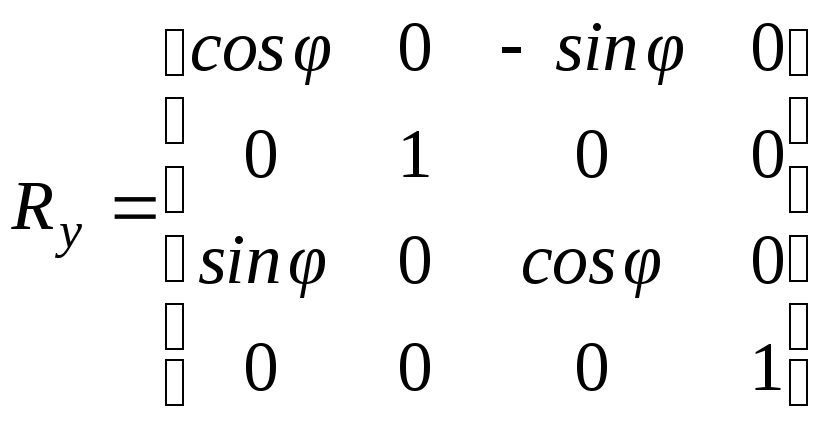• восстановим исходное направление прямой L. Для этого выполним поворот на угол 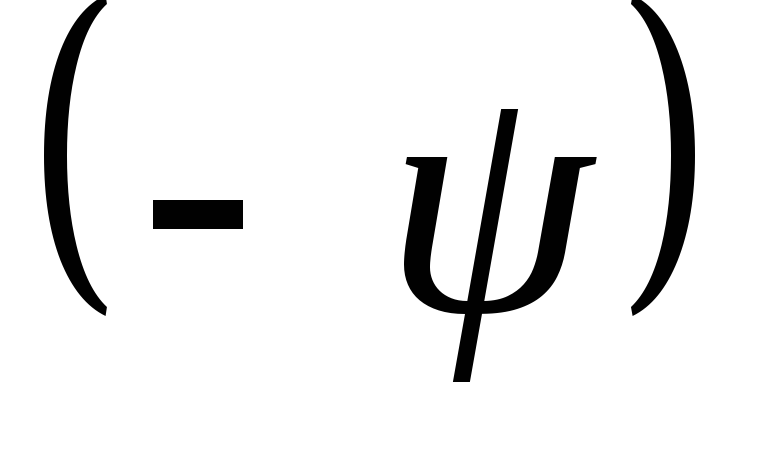вокруг осиZ. Матрица преобразования будет обратной к матрице R_z и получается из нее заменой угл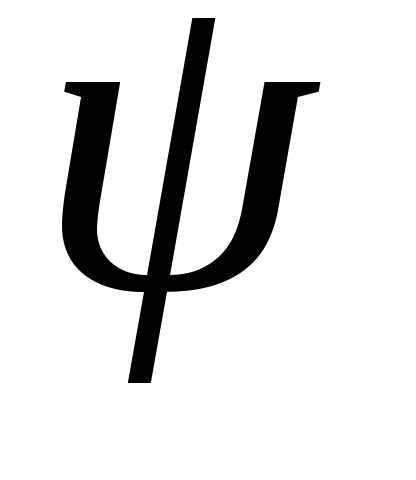а на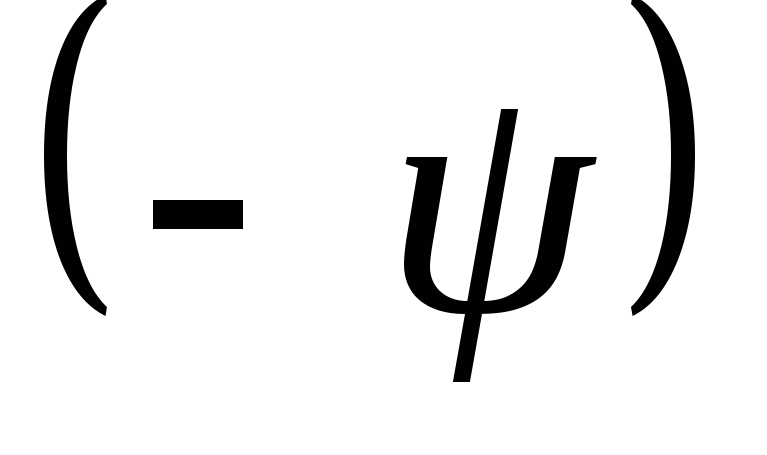. Отсюда получаем:

.

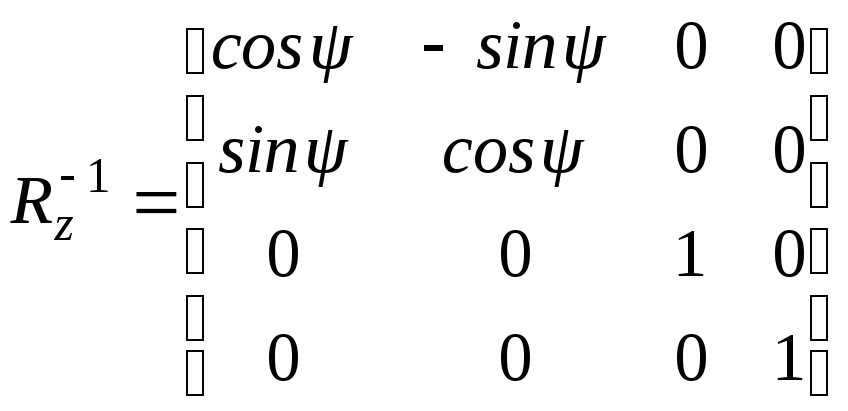• восстановим исходное положение прямой L. Для этого осуществим перенос на вектор A=(a, b, c). Соответствующая матрица T^-1 будет обратной к матрице T:

.

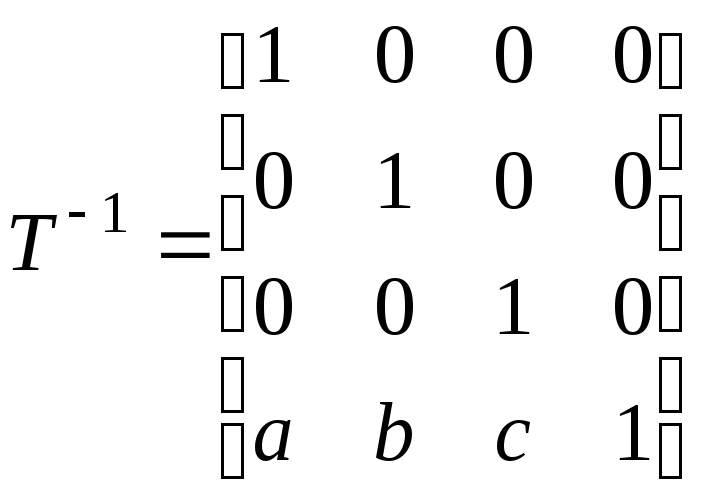Окончательная матрица заданного преобразования будет равна произведению матриц использованных элементарных преобразований, то есть . Например, при

При произвольных параметрах получается довольно громоздкое выражение.

ЛИТЕРАТУРА

1. Роджерс Д., Адамс Дж. Математические основы машинной графики/Пер. с англ.-М.: Машиностроение,2000.-240с.

2. Воеводин В.В. Линейная алгебра/-М.:Наука, 1980.

3. Курош А.Г. Курс высшей алгебры/-М.: 1962.

Содержание

45