1 4 3 4 3

1/2 8 6 4 3

1/3 12 9 4 3

:

1/10 40 30 4 3

:

1/100 400 300 4 3

:

Вектор с однородной компонентой h = 0 действительно представляет точку бесконечности и может быть также интерпретирован как движение к пределу (табл. 2-1).

Рассмотрим прямую у = (3/4)х и точку [X Y h] = [4 3 1]. Напомним, что в однородных координатах не существует единственного представления координатного вектора (табл. 2-1). Точка [4 3 1] представлена в однородных координатах по всем направлениям. Заметим, что в этой таблице при h 0 отношение y/x остается равным 3/4, как и требуется для сохранения уравнения. Кроме этого, обратим внимание на то, что следующая пара (x y), все точки которой располагаются на линии у = (3/4)x, быстро приближается к бесконечности. Таким образом, предел при h0 и есть точка бесконечности, заданная в однородных координатах как [X Y h] = [4 3 0].

Обратившись снова к рис. 2-15, легко продемонстрировать геометрическую интерпретацию процесса движения к пределу при h 0. Рассмотрим отрезок единичной длины, проходящий от точки начала координат в направлении [1 0] на плоскости h = s (s < 1). При s0 проекция этой прямой обратно на физическую плоскость h=1 в направлении лучей, проходящих через начало координат, становится бесконечной длины. Следовательно, конечная точка прямой должна представляться точкой бесконечности на оси X.

21. ПРАВИЛА ВЫПОЛНЕНИЯ ПРЕОБРАЗОВАНИЙ

Для представления данных и выполнения преобразований с помощью умножения матриц используются различные соглашения. Наибольшее внимание нужно уделять формулировке задач и интерпретации результатов. Например, перед выполнением поворота необходимо получить ответы на следующие вопросы.

В правосторонней или левосторонней системе координат определяются поворачиваемые координатные векторы?

Вращается объект или система координат?

Как определяются положительный и отрицательный повороты?

Координаты записываются в виде строки или столбца матрицы?

Вокруг какой линии или оси осуществляется поворот?

В данном изложении используется правосторонняя система координат, объект вращается в неподвижной координатной системе, положительный поворот определяется правилом правой руки, т. е. поворот по часовой стрелке осуществляется вокруг оси при наблюдении от начала вдоль положительной оси, и координатные векторы представляются в виде строки матрицы.

Выражение (2-29) задает преобразование для положительного поворота вокруг начала координат или оси z. Так как вектор задается строкой матрицы, то матрицу преобразования следует разместить после данных или матрицы координатных векторов. Это преобразование задается путем умножения справа. В случае однородных координат для положительного поворота объекта на угол вокруг начала координат (оси z) использование умножения справа приводит к следующему результату:

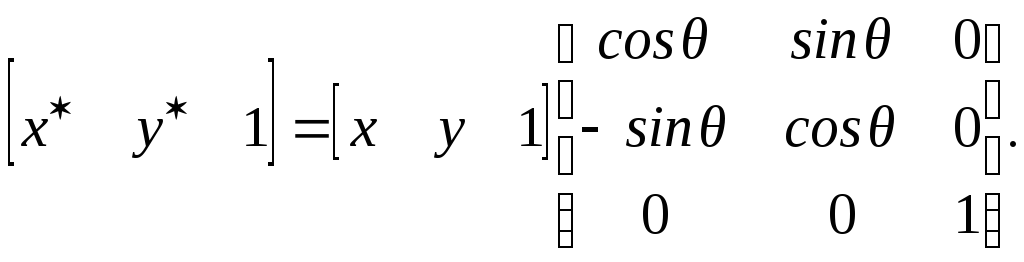(2-59)

Если мы подставим координатные векторы, заданные в однородных координатах в виде столбца матрицы, то поворот можно выполнить следующим образом:

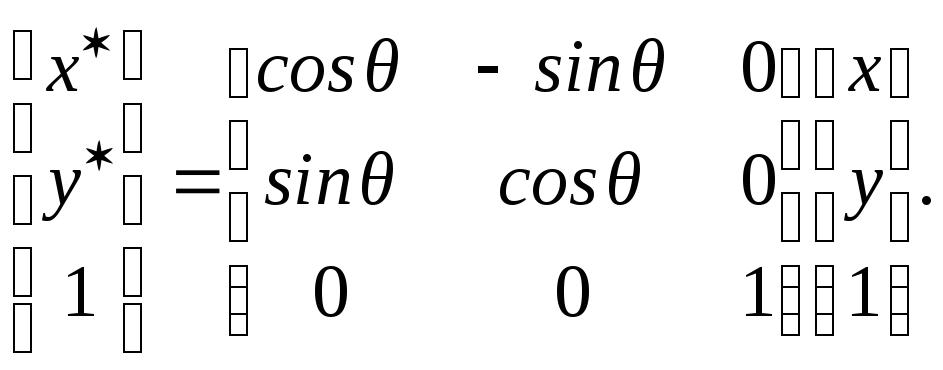(2-60)

Выражение (2-60) называется преобразованием с умножением слева, так как матрица преобразования расположена перед столбцом координатного вектора или данных.

Заметим, что (3 х 3)-матрица в выражении (2-60) есть транспозиция (3 х 3)-матрицы из выражения (2-59). Это свидетельствует о независимости строк и столбцов матрицы.

Для того чтобы повернуть систему координат и оставить неизмененными координатные векторы, необходимо в выражении (2-59) заменить  на -. Вспомним, что sin = - sin(-), a cos = cos(-).

Теперь выражение (2-59) будет иметь вид

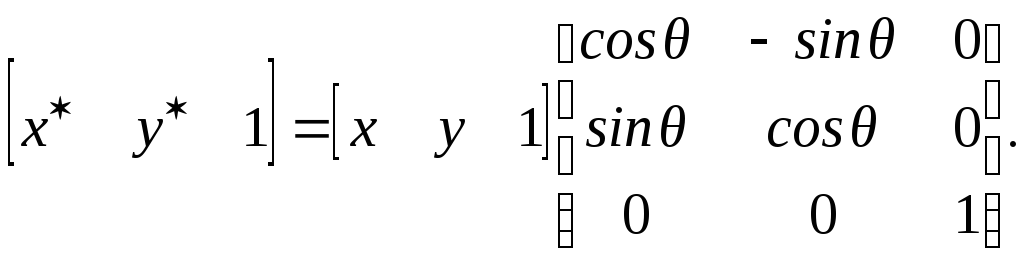(2-61)

Рис. 2-16 Эквивалентность преобразования координатных векторов и систем координат.

Заметим, что (3 х 3) матрица опять имеет обратную и также транспонируется в матрицу из (2-59).

Если вращается система координат и используется левосторонняя координатная система, то замену на надо производить дважды, а уравнение (2-59) снова оказывается справедливым при допущении, что применяется последующее умножение на строку матрицы данных.

Заметим, что, как показано на рис. 2-16, вращение против часовой стрелки векторов, задающих объект, идентично повороту в том же направлении координатных осей при неподвижном объекте. Опять нет необходимости в изменении содержимого матрицы преобразования 3x3, если нет других причин для ее редактирования. Эти несколько примеров показывают, насколько аккуратно необходимо выполнять матричные преобразования.