
книги / Остаточные напряжения в полимерных композиционных материалах
..pdfв (6.3) констант по известным свойствам волокна и связующего, а также численный эксперимент по проверке адекватности данной методики описаны в разделе 4.3.
T
При отсутствии армирующих элементов εTiig = εTii(1) = εTii(2) = α(T)dT ,
TH
где α – ЛКТР связующего и соотношения (6.3) переходят в (2.23), полученныеранеедля стеклующегося полимера.
6.1.2. Изменение жесткостных свойств композиционного материала в процессе стеклования связующего
Методика построения физических соотношений для композиционного материала со стеклующейся матрицей (6.3), использованная в предыдущем разделе, в основе своей содержит понятие свободной энергии. Подход не учитывает анизотропию влияния степени стеклования материала на его жесткость. Если для изотропных полимеров такое влияние полностью отсутствует, то в случае композитов со значительным разбросом свойств по направлениям оно может оказаться существенным. Предлагаемый в настоящем разделе подход, учитывающий эволюцию жесткостных свойств композита в процессе стеклования связующего, позволяет устранить указанный недостаток.
Рассматривается процесс неизотермического деформирования композиционного материала. Пусть в начальный момент времени он разогрет выше интервала стеклования. Композит в этих условиях
ведет себя как упругая среда со свойствами 4Сˆ (0,T ), αˆ (0,T ). Здесь
4Сˆ − тензор четвертого ранга жесткостных свойств среды; αˆ – тен-
зор второго ранга эффективных линейных коэффициентов температурного расширения. В качестве второго аргумента для обоих тензоров выступает температура, первого – степень застеклованности. Пусть в момент t1 , соответствующий вхождению в интервал стекло-
вания (T (t1 ) ≤ Tg1 ), в результате понижения температуры на T1
151
произошло образование новых связей пропорционально N (t1 ), которое, в свою очередь, приводит к наращиванию жесткости мате-
риала на величину |
4 |
ˆ |
|
|
|
4 |
ˆ |
в виде следующей суммы: |
|||||
|
C . Представим |
C |
|||||||||||
|
4 ˆ |
(N (t1 ),T (t1 )) = |
4 ˆ |
|
|
|
|
4 |
ˆ |
||||
|
C |
|
CT (N (t1 ),T (t1 )) + |
|
CN (N (t1 ),T (t1 )), (6.8) |
||||||||
где |
4 |
ˆ |
4 |
ˆ |
|
N; |
4 |
ˆ |
4 ˆ |
/ dt |
t − |
4 ˆ |
|
|
CN |
= ∂ |
C / ∂N |
|
|
CT |
= d C |
CN . Величина второ- |
|||||
го слагаемого определяется увеличением жесткости стеклующегося композита за счет вновь образованных в связующем межмолекулярных связей. Их естественное состояние совпадает с актуальным состоянием материала в момент возникновения (наращивание без натяга [27]). Поэтому для приращения тензора напряжений можно записать
|
|
σ(t1 ) = CT (N (t1 ),T (t1 )) |
|
ε(t1 ) + C (N (t1 ),T (t1 )) |
|
εT (t1 ), |
|||||
|
|
|
|
4 ˆ |
|
|
|
4 ˆ |
|
|
|
|
|
ˆ |
|
|
ˆ |
ˆ |
|||||
|
|
|
|
|
|
||||||
|
|
T |
|
|
(τ),T (τ))dN (τ), |
|
|
|
|
||
|
ˆ |
ˆ |
|
ˆ |
ˆ |
|
ˆ |
||||
где ε = ε − |
α(N |
ε – тензор деформаций; σ – тензор |
|||||||||
|
|
TH |
|
|
|
|
|
|
|
|
|
напряжений, |
ˆ |
– приращение тензора деформаций до момента по- |
|||||||||
ε |
|||||||||||
следующего изменения степени застеклованности. Для произволь-
ного момента ti с соответствующей температурой Tg2 |
< T (ti ) < Tg1 |
||||||||||
и степенью стеклования 0 < N (ti )< 1 зависимость σ = f ( ε) |
будет |
||||||||||
иметь вид |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
4 ˆ |
|
ˆ |
T |
|
4 ˆ |
|
ˆ |
T |
|
|
|
)) |
|
(ti ) + |
CT (N (ti ),T (ti )) |
|
(ti ). |
(6.9) |
||||
σ(ti ) = C (N (ti ),T (ti |
ε |
|
|
ε |
|
||||||
Значения напряжений в произвольный момент времени tk |
опре- |
||||||||||
деляются путем суммирования «предыстории» процесса: |
|
|
|
||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
ˆ |
|
) = |
ˆ |
|
|
|
|
(6.10) |
|
|
|
σ(tk |
σ(ti ). |
|
|
|
|
||||
i=0
После подстановки (6.9) в (6.10) получим с учетом (6.8)
152
|
|
k |
|
4 |
|
ˆ |
|
(N (ti ),T (ti )) |
|
|
|
|
|
|
|
4 |
ˆ |
|
(N (ti ),T (ti |
)) |
|
|
|
|
|
|
|||||||||||
(tk ) |
= |
|
|
|
ε(ti ) + |
|
|
|
|
ε |
(ti ) − |
||||||||||||||||||||||||||
|
|
C |
|
|
C |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
||||||||
|
i=0 |
|
|
|
|
|
|
− |
CN |
(N (ti ),T (ti )) |
|
ε(ti ) . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
(6.11) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Осуществление предельного перехода приводит к интегральной |
|||||||||||||||||||||||||||||||||||||
форме записи физических уравнений (6.11). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
= |
4 ˆ |
( |
N (t ),T (t ) |
) |
|
|
|
|
|
− |
N(t ) 4 |
ˆ |
|
( |
N ( |
|
),T ( |
|
) |
) |
|
|
|
|
|
|
|
)dN, (6.12) |
|||||||
σ |
|
|
ε |
|
N |
τ |
τ |
|
ε |
τ |
|||||||||||||||||||||||||||
ˆ (t ) |
|
C |
|
|
ˆ (t ) |
|
|
|
C′ |
|
|
|
|
ˆ ( |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
ˆ′ |
|
∂ |
4 |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|||
|
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где |
СN |
= |
|
∂N |
|
Запишем выражение для текущей жесткости мате |
|||||||||||||||||||||||||||||||
риала с использованием разложения (6.8): |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
4 ˆ |
|
|
|
|
(t ),T (t )) = |
4 ˆ |
|
|
|
|
|
N(t ) |
4 ˆ |
|
(N (τ),T (τ))dN. |
||||||||||||||||||||
|
|
C (N |
C (0,T |
(t )) + |
|
CN′ |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подстановка данного выражения в (6.12) с последующим приведением подобных позволяет записать определяющие соотношения в другой форме:
|
|
σ |
|
(t ) = C (0,T (t )) |
|
ε |
|
(t ) + |
|
|
|
||||||||||||
|
|
ˆ |
g |
|
|
4 ˆ |
|
|
|
|
|
|
ˆ |
g |
|
|
|
|
|
|
|
||
N(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
ˆ |
( |
N ( |
|
),T ( |
|
) |
) |
|
|
g |
(t ) |
|
|
g |
( |
|
|
|
||||
+ |
τ |
τ |
ε |
− ε |
τ |
|
(6.13) |
||||||||||||||||
|
N |
|
|
||||||||||||||||||||
|
|
C′ |
|
|
|
|
ˆ |
|
|
ˆ |
|
|
) dN. |
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения (6.13) верны для охлаждения материала от TH |
> Tg 1 , |
||||||||||||||||||||||
поэтому в начальный момент времени степень стеклования N (0) = 0
и в (6.13) проведена замена соответствующего предела интегрирования. Индекс «g» обозначает стеклование. Будем далее полагать, что после охлаждения до температуры TH < Tg2 по программе де-
формирования (6.13) композит начинает нагреваться. Связи, возникшие при отверждении, с «замороженными» актуальными дефор-
153
мациями разрушаются. Пусть в момент ti , соответствующий степени стеклования и температуре Ti , в результате роста температуры исчезла некоторая доля связей Ni . По аналогии с (6.9) запишем выражение для приращения напряжения до момента следующего из-
менения температуры: |
|
|
|
(ti ) + CT (Ni ,T (ti )) |
|
|
|
(ti ) + |
|||||||||||
σ = C (N |
(ti ),T (ti )) |
|
ε |
|
|
ε |
|
||||||||||||
ˆ |
h |
4 ˆ |
|
ˆ |
h |
|
|
|
|
|
4 ˆ |
|
|
ˆ |
h |
|
|||
|
4 ˆ |
|
|
|
|
|
|
h |
g |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
ˆ |
|
ˆ |
|
|
|
|
||||||
|
|
+Δ |
CN (N (ti ),T (ti )) |
|
ε |
|
(ti ) − ε |
|
(ti ) . |
|
|
|
(6.14) |
||||||
Деформации и приращения деформаций с индексом «h» соответствуют стадии нагрева. Разность в последнем члене правой части (6.14) означает, что исчезновение Ni связей приводит к высвобож-
дению «замороженных» при стекловании деформаций, в результате чего появился скачок напряжений, пропорциональный разности актуальных деформаций, соответствующих N (ti ) при размягчении
и отверждении. Это объясняется тем, что естественное состояние данного числа связей тождественно актуальному состоянию среды
в момент их возникновения. |
Выражая |
4 |
ˆ |
через |
4 ˆ |
, |
4 ˆ |
как |
|
CT |
CN |
C |
|||||
в (6.8), преобразуем (6.14) к виду |
|
|
|
|
|
|
|
|
|
σ |
|
(ti ) = C (N (ti ),T (ti )) |
|
ε |
|
(ti ) + |
|
|
||||||||||||||
|
|
ˆ |
h |
|
4 ˆ |
|
|
|
|
|
|
|
ˆ |
h |
|
|
|
|
|
|
|
||
+ |
C (N |
|
|
|
|
|
|
|
|
|
|
|
|
)) |
|
|
|
|
(ti ) + |
||||
(ti |
),T (ti )) − |
|
CN (N (ti ),T (ti |
|
|
ε |
|
||||||||||||||||
|
4 ˆ |
|
|
|
|
4 |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4 |
ˆ |
|
|
|
|
|
|
h |
|
|
|
|
|
g |
|
|
|
|
|
||
|
|
|
|
|
ˆ |
|
|
|
|
ˆ |
|
|
|
|
|||||||||
|
+Δ CN (N (ti ),T (ti )) |
|
|
(ti ) − |
|
(ti ) . |
|
|
|||||||||||||||
|
|
ε |
|
ε |
|
|
|
||||||||||||||||
После приведения подобных и осуществления перехода вначале к интегральной сумме, а затем к интегралу, получим выражение связи между напряжениями и деформациями при размягчении композита:
|
h |
(t ) |
|
4 ˆ |
( |
N (t ),T (t ) |
) |
|
|
|
|
h |
(t |
) |
|
N(t ) |
4 ˆ |
|
|
|
|
( |
|
),T ( |
|
) |
) |
|
|
g |
( |
|
)dN ( |
|
) |
|
||||||||||
ˆ |
|
|
|
|
ˆ |
|
|
|
|
|
|
N |
|
|
ˆ |
|
|
|
||||||||||||||||||||||||||||
|
= |
C |
|
|
|
− |
|
|
|
C′ |
|
|
τ |
τ |
|
τ |
τ |
− |
||||||||||||||||||||||||||||
σ |
|
|
|
|
|
|
|
|
ε |
|
|
|
i |
|
|
|
|
|
N ( |
|
|
|
|
|
|
|
|
ε |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
ˆ |
|
( |
N ( |
|
),T ( |
|
) |
) |
|
|
g |
( |
|
)dN ( |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
− |
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
C′ |
τ |
τ |
|
τ |
τ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
154
Объединение двух интегралов в правой части дает окончательный вид прямых физических соотношений:
σ |
|
(t ) = C (N (t ),T (t )) |
|
|
ε |
|
(ti ) − |
|
||||||||||||
ˆ |
h |
|
4 ˆ |
|
|
|
|
|
|
|
|
|
ˆ |
h |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
N(t ) |
4 ˆ |
|
|
|
|
|
) |
|
|
|
g |
|
|
|
|
|
|
|
|
|
− |
|
τ |
|
τ |
|
|
ε |
|
τ |
|
|
|
τ |
|
|
|||||
N ( |
N ( |
),T ( |
) |
|
|
( |
)dN ( |
). |
(6.15) |
|||||||||||
|
|
C′ |
|
|
|
ˆ |
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.1.3. Сравнение полученных типов определяющих соотношений
Уравнения связи между напряжениями и деформациями для полимерных стеклующихся композитов, вывод которых осуществлялся методом наращивания жесткости (6.14), (6.15), являющиеся более общими по отношению к соотношениям (6.3), а следовательно, более точно описывающие процессы стеклования и размягчения, неудобны
впрактическом применении. Главный их недостаток заключается
внеобходимости точного определения производной тензора жестко-
сти по степени стеклования и зависимостей тензоров 4Сˆ (N ), εˆT (N ).
При численном расчете термомеханических характеристик композиционного материала это приводит к неоправданно большим затратам машинного времени и памяти ЭВМ, а при использовании в численных расчетах краевых технологических задач – к потере точности изза неизбежности огрубления вычисления производной при дискретизации задачи по времени. Поэтому на практике предпочтительнее пользоваться более простыми выражениями типа (6.3).
Определим класс композиционных материалов, для которых соотношения (6.3) дают точное описание, т.е. совпадают с (6.14). Представим оба типа уравнений в покомпонентной записи. С помощью использования свободной энергии вариант имеет вид
|
|
э |
(1) |
|
|
(1) |
|
+ |
|
|
σij (t ) = Cijkl |
(t ) εkl (t ) |
− εTkl (t ) |
|
|||||
|
N(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
(t ) |
εkl (t ) − εkl (τ) |
(2) |
|
(2) |
|
(6.16) |
||
+Cijkl |
− εTkl |
(t ) + εTkl (τ) dN (τ). |
|||||||
|
0 |
|
|
|
|
|
|
|
|
155
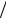
Полученный на основе записи эволюции жесткостных свойств вариант:
σijж (t ) = Cijkl (N (t ),T (t )) εkl (t ) − εTkl (N (t ),T (t )) −
N(t ) |
|
( |
|
) |
− εTkl ( |
N ( |
|
),T ( |
|
) |
|
( |
N ( |
|
),T ( |
|
) |
) |
dN ( |
|
). (6.17) |
− |
|
τ |
τ |
τ |
C′ |
τ |
τ |
τ |
|||||||||||||
εkl |
|
|
|
|
|
) Nijkl |
|
|
|
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ставится задача определения вида функций Сijkl , εkl , при которых σijэ = σijж . Для упрощения преобразований полагаем, что на ин-
тервале стеклования зависимость компонентов тензоров упругости материала от температуры пренебрежимо мала по сравнению с изменением жесткости за счет стеклования связующего. Чтобы найти вид зависимости Сijkl , обеспечивающий переход (6.17)
в (6.16), необходимо приравнять правые части этих выражений без учета температурной деформации (вклад температурной деформации по условию эквивалентен для обеих формул и сокращается при их приравнивании).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сijkl(1)εkl (t ) + Сijkl(2)εkl |
(t ) N (t ) − Сijkl(2) |
εkl (τ) dN (τ) = |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= Cijkl (N (t ),T (t ))εkl (t ) − |
|
|
εkl (τ)CN′ ijkl (N (τ),T (τ))dN |
(τ). |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продифференцировав по времени, получим |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
(1) |
|
|
|
(2) |
|
N |
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Сijkl εkl |
+ Сijkl |
(εkl |
|
|
+ |
εkl |
|
)− Сijkl εkl |
|
= |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
= |
C |
|
|
|
C |
|
− εkl |
C |
. |
|
|
|
|
|
|
|
|
(6.18) |
|||||
|
|
|
|
|
|
|
ijkl εkl + |
|
ijkl |
εkl |
ijkl |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аргументы |
опущены |
для |
|
сокращения |
|
записи. |
|
При |
выводе |
|||||||||||||||||||||
(6.18) |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 ˆ |
|
|
4 |
ˆ |
|
|
, |
|
- |
учитывалось |
что в интервале стеклования |
C′ |
>> |
|
C′ |
и |
сле |
|||||||||||||||||||||||
|
|
N |
|
T |
|
|
||||||||||||||||||||||||
|
|
, |
ˆ |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.18) |
|
|
|
|
|||
довательно |
C′ |
dC dt . |
После приведения подобных |
будет |
||||||||||||||||||||||||||
|
N |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
иметь вид
156
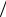
Cijkl = Cijkl(1) + Cijkl(2) N. |
(6.19) |
Таким образом, для того чтобы соотношения (6.16) совпадали с соотношениями (6.17) при описании поведения стеклующегося композиционного материала, зависимость компонент тензора упругости от степени застеклованности должна подчиняться закону (6.19).
Для определения функциональной зависимости компонент тензора свободных деформаций εTkl (N,T ), обеспечивающей тождест-
венность (6.16), (6.17), приравниваются правые части этих выражений с учетом того, что для выбранного типа тензора упругости (6.19) суммы членов, содержащих активные деформации по обе стороны от знака равенства, тождественны:
(1) (1) |
(2) |
N(t ) |
(2) |
|
(2) |
|
|
−Cijkl εTkl (t ) = Cijkl |
|
εTkl |
(t ) − εTkl |
(τ) dN (τ) = |
|||
|
|
0 |
|
|
|
|
|
= − Cijkl(1) + Cijkl(2) N (t ) εTkl (t ) + Cijkl(2) |
N(t ) |
(τ)dN (τ). |
|||||
|
εTkl |
||||||
|
|
|
|
|
0 |
|
|
На основании принятых допущений после дифференцирования данного выражения по времени и приведения подобных получаем систему линейных дифференциальных уравнений первого порядка с разделяющимися переменными относительно εTkl :
|
|
|
|
|
|
|
C |
(1) |
+ C |
(2) |
N |
|
= C |
(1) |
|
(1) |
+ C |
(2) |
|
(2) |
N. |
|
|
(6.20) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
εkl |
|
ijkl |
|
ijkl |
|
|
|
ijkl |
εTkl |
|
ijkl |
εTkl |
|
|
|
|
|
|
||||||||||||
|
Для трансверсально изотропных и ортотропных композитов |
||||||||||||||||||||||||||||||||||
можно |
в |
явном |
виде |
разрешить |
|
систему |
|
(6.20) относительно |
|||||||||||||||||||||||||||
|
d |
|
dt . |
|
|
|
|
|
|
|
|
|
|
|
{ |
} = [C]−1 |
{ |
} , |
|
|
|
|
[C] – |
|
|
|
|||||||||
εTkl |
≡ |
εTkl |
|
|
В этом случае |
|
|
|
ε |
|
|
C(2) |
εT |
|
|
|
где |
|
|
квадратная |
|||||||||||||||
|
|
|
|
|
|
|
|
3 |
× |
3; C |
= |
C(1) |
+ |
N ; { |
|
} – |
|
- |
|
, |
|||||||||||||||
матрица |
размером |
|
|
|
|
ij |
|
|
ijkl |
|
|
ijkl |
|
|
|
εT |
|
|
|
вектор столбец |
|||||||||||||||
|
|
|
|
C |
(1) |
(1) |
+ |
C |
(2) |
(2) . |
Обозначив через |
C |
|
обратную к |
[C] |
||||||||||||||||||||
причем εTi = |
iijj |
εTjj |
|
iijj |
εTjj |
|
|
|
|
||||||||||||||||||||||||||
матрицу, получим в явном виде выражения для компонент тензора свободной деформации:
157

|
|
0 |
t |
C |
|
dt , |
|
(6.21) |
|
|
εii = |
|
ij |
εTj |
|
|
|
|
|
|
0 |
|
|
|
|
|
где C11 = (C22 )2 |
− (C23 )2 |
; |
C12 |
= |
C12 (C23 |
− C22 ) |
; |
|
|
|
|
|
|
|
|
|
|
C23 = (C12 )2 − C11C33 |
; |
C22 = C11C22 − (C12 )2 |
; |
|||||
= 2(C23 )2 (C12 − C22 ) + C33 ((C22 )2 − (C12 )2 ). |
|
|||||||
Формула (6.21) дает зависимость температурной деформации от времени, обеспечивающую переход от физических соотношений (6.17) к соотношениям (6.16) и обратно.
Выражения (6.19), (6.21) позволяют выделить класс композитов, для которых оба подхода дают аналогичный результат. Наиболее очевидный пример – композит, не содержащий наполнителя. В остальных материалах такое совпадение может быть результатом случайной комбинации свойств волокна и связующего. Поэтому представляет интерес оценка погрешности, вносимой в расчеты при использовании упрощенных соотношений (6.3). Проведем сравнение моделей для осреднения термомеханических свойств композиционного материала по Фойхту и Рейссу.
Обозначим индексом «m» параметры, относящиеся к связующему (матрице), а индексом «a» – к волокну (арматуре). Будем полагать, что модули связующего и волокна, а также коэффициенты температурного расширения αm , αa не зависят от температуры.
Программа деформирования включает: охлаждение защемленного образца от T > Tg1 до Tk < Tg2 , разгрузку при T = Tk ; повторное за-
щемление и разогрев до TH . В соответствии с (6.16), (6.17) напряжения в охлаждаемом образце будут меняться по закону (индекс «g», как и ранее, обозначает стеклование):
|
σэg (T ) = −E(1)εT(1) − E(2) × |
|
|
|
|
N(t ) |
|
|
|
× εT(2) |
(T ) N (T ) − |
εT(2) (T (τ))dN (τ) |
; |
(6.22) |
|
0 |
|
|
|
|
|
|
|
|
158
σжg (T ) = −E (N (T ))εT (T ) +
N(t )
|
+ εT (T (τ))EN′ (N (τ))dN (τ). |
|
(6.23) |
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Разгрузка и последующий разогрев материала до первоначаль- |
|||||||||||||
ной температуры сопровождаются появлением напряжений: |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
N(t ) |
|
|
σэh (T ) = −E(1)εT(1) (T ) − E(2) εT(2) (T ) N |
+ |
εT(2) (T (τ))dN (τ) |
+ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
+ E |
(2) |
|
|
|
ε |
э |
(Tk ); |
|
(6.24) |
|
+ E |
|
|
N (T ) |
|
|
|
||||||
σ |
|
(T ) = E (T ) ε |
|
(Tk ) |
− εT (T ) + |
|
|
||||||
|
жh |
|
|
|
|
|
ж |
|
|
|
|
|
|
|
N(t ) |
|
(T (τ))EN′ (T |
(τ))dN (τ), |
|
|
|||||||
|
+ εT |
|
(6.25) |
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
где εэ (Tk ), εж (Tk ) – деформация после разгрузки охлажденного ма-
териала: εэ (Tk ) = −σэg (Tk )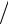 (E(1) + E(2) ); εж (Tk ) = −σжg (Tk )
(E(1) + E(2) ); εж (Tk ) = −σжg (Tk )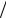 E (Tk ).
E (Tk ).
Значения эффективных термомеханических характеристик из (6.23)–(6.26) зависят от способа осреднения свойств композита. Рассмотрим деформирование вдоль волокон, расчетная схема которого представлена на рис. 6.1, а. Обозначим через ψ коэффициент объемного содержания волокна, а через ψ – связующего. В этом случае
σ = σa ψ+ σmψ; |
εa = εm = ε. Индекс «m» относится к матрице, «a» – |
||||||||
к арматуре. Эффективные параметры определяются по формулам |
|||||||||
ε(N ) = Em ψ+ Ea ψ; ε0 = T (ψαm Em + ψEaαa )(Em ψ+ Ea ψ)−1 dt; |
|||||||||
|
|
|
|
TH |
|
|
|
|
|
|
|
|
|
E(1) = Em(1)ψ+ Ea ψ; |
E(2) = Em(2)ψ; |
|
|
||
(1) |
T |
|
(1) |
(1) |
|
|
−1 |
(2) |
T |
εT |
= |
Em |
αmψ+ Eaαa ψ Em |
ψ+ Ea ψ |
dT; |
εT |
= αmdT , |
||
|
TH |
|
|
|
|
|
|
|
TH |
159
где Em(1) равновесный модуль связующего; Em(2) = Emg − Em(1); Ea ,αa , Em , αm – модули и ЛКТР арматуры и связующего соответственно;
Em = Em(1) + Em(2) N; ψ = 1− ψ.
После подстановки в (6.23)–(6.26) оказывается, что соотношения (6.16) и (6.17) дают одинаковые значения напряжений:
T(t )
σэ//g (T ) = σж//g (T ) = − Em(1) + Em(2) N (τ)ψαm + Ea ψαa dT (τ);
TH |
|
σэн// (T ) = σжн// (T ) = ε(Tk )[ψEm + ψEa ]+ σэ//g (T ), |
(6.26) |
где ε(Tk ) = −σэg (Tk )(ψ(Em(1) + Em(2) )+ ψEa )−1 . Точные эффективные
напряжения рассчитываются путем решения задачи о совместном деформировании матрицы и волокна. Система уравнений при этом включает в себя определяющие уравнения, уравнения равновесия и совместности деформаций:
|
N(t ) |
|
|
σm (T ) = Em (T ) εm (T ) |
− Em(2) εm |
(τ) dN (τ); |
(6.27) |
|
0 |
|
|
σa (T ) = Ea εa (T ); |
|
|
|
σ(T ) = σa (T )ψ+ σM (T )ψ; |
ε(T ) = εa (T ) = εM (T ). |
(6.28) |
|
(см. рис. 6.1, 6.2).
Решая (6.27), (6.28) с учетом условий режима деформирования и изменения температуры, получим эффективные напряжения, совпадающие с (6.26). Таким образом, соотношения (6.16) и (6.17) дают для данной расчетной схемы точное решение.
Такого совпадения не наблюдается при деформировании поперек волокон (осреднение по Рейссу, см. рис. 6.1, б). В этом случае эффективные характеристики материала находятся по формулам
160
