книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)

1.2. КИНЕМАТИКА

Девиатор деформаций (1.2.84)

Dε =[[eik ]] = Tε −Sε = εik − 13 εδik

или

Самостоятельно выполнить проверку правильности вычисления компонент девиатора деформации.

3. Для нахождения главных компонент тензора деформаций решим характе# ристическое уравнение (1.58) его матрицы

|εik – λδik| = 0

или

–λ3 + εIλ2 – εIIλ + εIII = 0,

где первый εI, второй εII и третий εIII инварианты тензора деформаций опреде# ляются соотношениями

Раскрывая определитель в характеристическом уравнении, найдем:

(0,12 – λ)(– 0,12 – λ)(0,1875 – λ) – 0,0256 (0,1875 – λ) = 0.

Отсюда видно, что первый корень характеристического уравнения λ1 = 0,1875, а остальные его корни определим из квадратного уравнения λ2 = 0,04. Отсюда λ2 = + 0,2; λ3 = – 0,2. Располагая компоненты тензора деформаций с соблюде# нием условия (1.2.79)

61

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

ε1 ≥ ε2 ≥ ε3,

найдем диагонализированный вид матрицы тензора деформаций

0,2 0 0

Tε = 0 0,1875 0 . 0 0 −0,2

Самостоятельно выполнить проверку правильности диагонализации тензора деформации.

4. Для вычисления интенсивности сдвиговых деформаций можно воспользоваться формулами (1.2.87) или их модификацией:

Вычисление по одной из формул для определения Г, например последней, позволяет получить

1.2.5. Условие совместности деформаций

Предполагается, что исходное недеформированное в момент времени t0 и деформированное в произвольный момент времени t состояния всегда рассматриваются в евклидовом пространстве. Из геометрии Г. Римана известно, что математически это предположение относительно компонент градиентов (1.2.13), (1.2.19) и компонент тензоров (1.2.28), (1.2.40), (1.2.46), (1.2.57) записывается в виде равенства нулю тензора Г. Римана–Э.Б. Кристоффеля (П1.99) либо в лагранжевых, либо в эйлеровых координатах. Решение задач с использованием таких соотношений выходит за рамки излагаемого курса. Для малых деформаций (1.2.70) равенство нулю компонент тензора (П1.99) эквивалентно условию

На основании (П1.88) подстановка (1.2.70) в (1.2.88) приводит к тождеству. Это означает, что при решении задач МСС в перемещениях нет необходимости проверять выполнение условия (1.2.88), когда тензор деформаций определяется по формуле О. Коши (1.2.70). При решении же этих задач в малых деформа-

62

1.2. КИНЕМАТИКА

циях на тензор Tε должны быть наложены ограничения в виде соотношения (1.2.88), которое называется условием Б. Сен Венана или в данном случае усло вием совместности деформаций. С математической точки зрения выполнение соотношения между компонентами тензора деформаций Tε в (1.2.88) является необходимым и достаточным условием интегрируемости множества уравнений О. Коши (1.2.70) относительно компонент вектора перемещения (П1.6), кото-

рые вычисляются по обобщенной формуле Е. Чезаро (П1.108) с заменой в ней a

a0 на U0 , Tc0 на Tω0 и Tb на Tε:

– значения вектора перемещенияU и тензора жесткого поворота Tω соответственно в начале пути интегрирования при x = x0 .

Определение вектора перемещения U по тензору деформаций Tε с помощью формулы (1.2.89) удобно лишь тогда, когда этот тензор удовлетворяет уравнению совместности деформаций Б. Сен-Венана (1.2.88). В противном случае интегрирование может быть трудно выполнимым. Это является основной причиной редкого применения решения задач МСС в деформациях.

1.2.6. Поле скоростей

По определению скорость перемещения материальных частиц вычисляется по формуле (1.2.15). Учитывая (1.2.4) и (1.2.10), вектор скоростиV можно также рассчитать по формуле

V ≡ Tδ V. На практике наибольший интерес представляет раскрытие полной про-

n

изводной (1.2.10) с помощью (1.2.16), где вместо Ta нужно подставить (1.2.9):

63

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Отсюда, решая замкнутую относительно компонент Vi вектора скоростиV

систему, приходим к формуле И. И. Гольденблата

где компоненты Di вспомогательного вектора D получаются из якобиана (1.2.20) путем замены дифференцирования лагранжевых координат по координате Ei дифференцированием по времени t. Если такую замену дифференцирования выполнить в декартовых координатах, то компоненты вспомогательного вектора будут иметь вид

Для произвольных координат вспомогательный вектор

Подстановкой (1.2.94) в (1.2.92) получим окончательный вид формулы, предложенной в кинематике Б. В. Кучеряевым, для определения вектора скорости по заданному закону движения (1.2.9) в эйлеровых координатах:

64

В частном случае при выполнении (1.2.55) устанавливаем, что в окрестности материальной частицы, движущейся без изменения объема, поле скоростей должно быть соленоидальным:

Это соотношение называется условием несжимаемости сплошной среды. Выполнение условия постоянства объема (1.2.55) приводит (1.2.92) к виду

В частности, в декартовых прямоугольных координатах такой вектор имеет компоненты, совпадающие с точностью до знака с компонентами вектора D в формуле (1.2.93).

Каждая функция Li(Ek, t) в пространстве Ek при фиксированном времени t представляется семейством изоповерхностей Li = const. Если две такие функ-

ции, например L1 и L3, не зависят от времени ∂∂Lt1 = ∂∂Lt3 = 0, то геометрически

это означает, что вид изоповерхностей L1 = const и L3 = const в пространстве Ek не меняется по времени.

Упражнение 1.2.4. Показать, что при ∂∂Lt1 = ∂∂Lt3 = 0 формула (1.2.92) преобразуется к виду

65

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Ясно, что при выполнении условия (1.2.55), учитывая тождество (П1.85), из (1.2.101) получаем условие несжимаемости (1.2.98). Такое поле скоростей полностью определяется константой V0 и двумя функциями L1(Ei) и L3(Ei):

В гидродинамике обычно одну из лагранжевых координат, например L1, связывают с функцией тока Ψ, совпадающей с L1 с точностью до постоянного сомножителя и несущественной аддитивной константы:

В частности, при двухмерном течении, когда L3 = E3, из (1.2.104) имеем

Из теории векторных полей известно, что векторной линией называется пространственная линия, в каждой точке которой касательная к ней совпадает с направлением вектора в этой точке. Векторная линия поля скоростей называется линией тока. Следовательно, элемент длины dE линии тока колинеарен вектору скорости V : V ×dE = 0 . Отсюда, в соответствии с (П1.2), имеем

где dλ – скалярный параметр. В скалярной форме (1.2.106) имеет вид

Эти соотношения называются дифференциальным уравнением линии тока. Подобно соотношению (1.2.15) уравнения (1.2.106), (1.2.107) представим в виде

Отличие (1.2.15) и (1.2.108) состоит в том, что в (1.2.15) время t входит как в левую, так и в правую части равенства, а в (1.2.108) – только в правую часть.

66

1.2. КИНЕМАТИКА

Интегрирование (1.2.15) по времени позволяет рассчитать траекторию движения материальной частицы – линию, по которой перемещается эта частица. Таким образом, в общем случае линия тока и траектория материальной частицы не совпадают. Для стационарных полей скоростей (1.2.24) время как переменная величина не входит в первую часть соотношения (1.2.15). Поэтому для стационарных течений скалярные параметры dt в (1.2.15) и dΟ в (1.2.106) – (1.2.108) практически совпадают, что для таких течений приводит к совпадению понятий «траектория материальной частицы» и «линия тока».

Покажем, что в стационарных течениях на линии тока величины < и L3, входящие в (1.2.104), постоянны. Для этого подставим (1.2.104) в дифференциальное уравнение линии тока (1.2.107).

Упражнение 1.2.5. Показать, что вдоль линии тока величины < и L3 из (1.2.104) удовлетворяют соотношению

Обращение (1.2.109) в тождество может быть связано либо с равенством нулю дифференциалов < и L3

либо с пропорциональностью < и L3. Последнее невозможно, так как в соответствии с (1.2.103) функция < пропорциональна лагранжевой координате L1, и вследствие линейной независимости (П2.1) всех координат Li функция < не может быть пропорциональна двум другим лагранжевым координатам, в том числе и L3. Следовательно, (1.2.110) является единственным условием обращения (1.2.109) в тождество. Так как условия (1.2.110) выполняются вдоль линии тока, то это значит, что на этой линии имеем < = const и L3 = const, а сама линия тока находится на пересечении изоповерх-

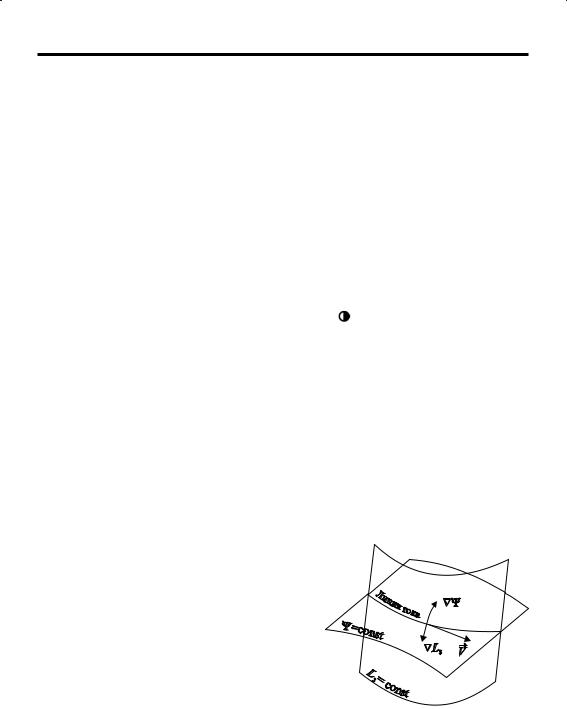
ностей <(Ei) = const и L3(Ei) = const (рис. 17).

67

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

лелепипеда с исходными размерами h0 ; b0 ; 0 и текущими размерами h; b; , в котором не происходит изменения объема ( h0b0 0 = hb ) и отношение начальной к текущей ширине равно отношению начальной к теку-

Пусть h = h(t) – изменение высоты параллелепипеда во времени t, удовлетворяющее начальному условию h(t0) = h0. В общем случае при осадке в направлении оси E1 с увеличением времени t происходит уменьшение текущей высоты h и соответствующее увеличение размеров b и . Закон движения (1.2.9) для рассматриваемой задачи может быть представлен в виде

Условия задачи позволяют записать лагранжевы координаты через высотные параметры

Тогда для начальных условий имеем h = h0 и Li = Ei, а из граничных условий на гранях параллелепипеда (L1 = h0; L2 = 0 ; L3 = b0 и E1 = h; E2 = ; E3 = b), учиты-

68

1.2. КИНЕМАТИКА

устанавливаем, что якобиан (1.2.20), составленный из компонент тензора

L , равен единице и условие задачи о неизменности объема параллелепи-

педа, выражаемое формулой (1.2.55), выполняется независимо от времени t. Поэтому вектор скорости (1.2.95) должен удовлетворять условию несжимаемости (1.2.98), а его компоненты в соответствии с (1.2.99) в эйлеровых координатах Ei определяются формулами (1.2.93):

Упражнение 1.2.6. Используя соотношение (1.2.111) и условия рассмотренной выше задачи об осадке параллелепипеда, построить поле скоростей в лагранжевых координатах Li.

Упражнение 1.2.7. Выполнить расчет компонент тензоров деформации по теориям конечных (1.2.42), (1.2.59) и малых деформаций (1.2.70). Показать, что во всех случаях поля деформаций являются однородными и не зависят от

получаемых при замене конечных деформаций малыми деформациями Закон движения (1.2.111) может быть использован для расчета параметров

осадки при плоской и осесимметричной деформациях.

В первом случае отсутствие движения в одном из направлений, например L2, обеспечивается равенством = 0 и его следствием L2 = E2. Тогда измене-

ние ширины полностью определяется условием постоянства объема b = b0 hh0 , а закон (1.2.111) принимает вид

69

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Во втором случае расчеты удобнее вести в цилиндрических координатах, для которых в индексированных переменных при подстановке значений индексов вместо цифр 1, 2, 3, как это делалось ранее, следует использовать буквы z, ϕ, ρ. При осесимметричной деформации Lϕ = Eϕ . Параметры b и b0 в законе движения (1.2.111) обозначим R и R0 соответственно. Тогда, учитывая условие постоянства объема для цилиндрического образца ( h0 R02 = hR2 ), закон (1.2.111) принимает вид

Таким образом, закон движения (1.2.111) при h = h(t) ≤ h0 позволяет с помощью формулы (1.2.95) построить нестационарное поле скоростей, соответствующее процессу осадки образца в условиях объемной и двухмерной (плоской или осесимметричной) деформаций.

Отметим, что формулы (1.2.111) и их частные виды (1.2.112), (1.2.115), (1.2.116) также можно использовать для построения поля скоростей, соответствующего процессу растяжения образца. Для этого необходимо представить закон h = h(t) так, чтобы с увеличением времени t происходило увеличение текущей высоты h и соответствующее уменьшение размеров b и . В общем случае закон нестационарного изменения высоты образца может быть представлен в виде

где h – абсолютное изменение высоты образца к конечному моменту времени tk; f(t) – положительная безразмерная непрерывная функция времени, удовлетворяющая условиям f(t0) = 0 и f(tk) = 1. При решении задач растяжения в правой части (1.2.117) ставится знак плюс, осадки – минус.

Для стационарных процессов, как отмечалось ранее, поле скоростей определяется по формуле (1.2.101), а при выполнении условия постоянства объема (1.2.55) – по формуле (1.2.102).

Пусть в (1.2.111) координата L2 линейно зависит от времени t:

а остальные лагранжевы координаты вследствие соотношений h = h(E2; E3) и b = b(E1; E2) зависят только от эйлеровых координат. Тогда, используя

70