книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)

1.2. КИНЕМАТИКА

функцию Ψ тока в виде (1.2.103), по формуле (1.2.104) для объемного течения в декартовых координатах Ei имеем

где в соответствии с (1.2.103) и (1.2.111)

Подстановкой (1.2.120) и L3 из (1.2.111) в (1.2.119) находим

Такое поле скоростей можно использовать для моделирования многих ста# ционарных и квазистационарных процессов ОМД, в которых в качестве моде# ли металла допустимо применение сплошной несжимаемой среды. Например, к таким процессам относятся прокатка прямоугольной заготовки в калибрах и в валках с гладкой бочкой (с постоянным радиусом Rв валков), прессование и во# лочение такой же заготовки в профилированный канал матрицы. В некоторых частных случаях, имеющих большое прикладное значение, вид поля (1.2.121) существенно упрощается. Нижеследующая серия упражнений посвящена та# ким случаям.

Упражнение 1.2.8. Металлическая полоса с поперечным сечением h0 × b0 про# пускается (прокатывается) между двумя вращающимися валками постоянного радиуса в направлении эйлеровой оси E2 так, что ее текущая высота h не меня# ется по длине бочки валка в направлении оси E3, т. е. h = h(E2). Показать, что в этом случае поле (1.2.121) принимает вид

71

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Такому случаю соответствует прокатка на гладкой бочке без учета прогиба и сплющивания валков.

Упражнение 1.2.9. При прокатке полосы наблюдается малозначимая депланация боковой поверхности в направлении оси E1, т. е. b = b(E2). Показать, что в этом случае поле (1.2.121) принимает вид

Отметим, что с математической точки зрения оба случая одинаковы. Поэтому с точностью до символики поля (1.2.122) и (1.2.123) совпадают. С физической точки зрения они различаются: первому случаю (1.2.122) соответствует прокатка металла в абсолютно жестких валках (без учета их прогиба и сплющивания), второму (1.2.123) – прокатка металла, когда бочкообразование (депланация в направлении оси E1) боковой поверхности проката пренебрежимо мало. На практике векторное поле скоростей (1.2.122) может быть использовано для моделирования горячей прокатки сортового и листового металла, когда деформация прокатного валка пренебрежимо мала по сравнению с деформацией прокатываемого металла, а векторное поле скоростей (1.2.123) – для моделирования холодной прокатки тонколистового металла, когда слабое искажение боковой поверхности проката в вертикальном направлении по оси E1 можно не учитывать в расчетах.

Упражнение 1.2.10. Показать, что при прокатке полосы на гладкой бочке абсолютно жестких валков, когда h = h(E2), и без учета уширения полосы, когда b = b0 = const, поля скоростей (1.2.122) и (1.2.123) совпадут и будут иметь вид

Такому полю скоростей соответствует прокатка в условиях плоской деформации, когда все кинематические параметры движения сплошной среды зави-

72

1.2. КИНЕМАТИКА

сят только от двух координат (в данном случае – от E1 и E2), а движение в направлении третьей оси координат (в данном случае – E3) отсутствует.

Для осесимметричных стационарных процессов ОМД, как и ранее, используем цилиндрические координаты Ez, Eϕ, Eρ, в которых лагранжева координата

а остальные лагранжевы координаты Lϕ, Lρ зависят только от эйлеровых координат. При этом Lϕ = Eϕ, а радиальную лагранжеву координату по аналогии с (1.2.111) представим в виде

где R0 и R – начальный и текущий радиусы круглой заготовки.

В цилиндрических координатах условие несжимаемости (1.2.98) в соответствии с определением скалярного произведения оператора набла на вектор (п. П 1.5) имеет вид

При записи компонент вектора скорости через функцию тока осесимметричного течения

условие несжимаемости среды (1.2.98), представленное в виде (1.2.127), обращается в тождество. В этом случае Ψρ и Lρ связаны соотношением

Подстановкой (1.2.126) в (1.2.129), а результата – в (1.2.128) находим компоненты вектора скорости стационарного осесимметричного течения несжимаемых сред:

73

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Такое поле скоростей может быть использовано при моделировании процессов прессования, волочения и прокатки круглых прутков из круглой заготовки. Если такими способами моделируется деформация полых изделий с наружным R и внутренним r текущими радиусами из полой заготовки с соответствующими начальными радиусами R0 и r0, то вместо (1.2.126) лагранжеву координату Lρ следует представить в виде

Далее, полагая, что R = R(Ez) и r = r(Ez), по формулам (1.2.128) определяем компоненты вектора скорости стационарного симметричного течения несжимаемых сред с внутренней полостью:

В заключение отметим, что окончательный вид приведенных полей скоростей, которые могут быть использованы для моделирования процессов ОМД, определяется видом функций, описывающих значения текущих размеров и формы деформируемой заготовки. В наиболее простом виде такие функции учитывают основные геометрические характеристики области течения металла. Соответствующие таким функциям поля скоростей рекомендуется использовать как основное решение, последующая корректировка (п. П3.1.1) которого позволяет кроме геометрических параметров исследуемого процесса ОМД учитывать реологическое поведение (п. 1.5) деформируемого металла. В п. П3.2 приведены примеры и даны общие методы построения таких полей. В частности, для моделирования процесса прокатки в условиях плоской деформации с аппроксимацией изменения теку-

74

1.2. КИНЕМАТИКА

щей высоты h полосы по произвольному закону, например по окружности (П3.55), может быть использовано векторное поле (П3.58).

В общем случае вид поля скоростей, соответствующий решению исследуемой задачи ОМД, определяется полнотой выполнения требований, оговоренных в постановке задачи (п. 1.4). Поле скоростей, удовлетворяющее всем требованиям постановки краевой задачи, будем называть реальным (действитель ным) полем (Р полем) скоростей. Как правило, Р-поля скоростей удается построить лишь в отдельных случаях. Чаще всего решение задачи сводится к поиску наилучшего приближения к Р-полю. Среди всех векторных полей, во множество которых обязательно входят Р-поля скоростей, выделим поля скоростей, удовлетворяющие кинематическим краевым условиям (для стационарных течений – кинематическим граничным условиям). Такие поля будем называть кинематически возможными полями (КВ полями) скоростей.

Для КВ-полей скоростей на некоторых поверхностях допускается разрыв (ска чок) вектора скорости за счет тангенциальной к этим поверхностям составляющей вектора скорости. Такие поля будем называть разрывными КВ полями скоростей.

Задачи к пп. 1.2.6

Задача 1.2.6.1. Движение сплошной среды представлено зависимостью вектора Л. Эйлера от компонент вектора Ж. Лагранжа и времени t:

где a и b – константы с размерностями, обратными единицам длины и времени соответственно. Определить компоненты вектора скорости в лагранжевых и эйлеровых координатах.

Решение. По заданному закону движения в лагранжевых координатах вектор скорости V находится наиболее просто, так как вследствие выполнения закона сохранения материальных частиц (1.2.10) в этих координатах полная и частная производные тензорных величин по времени t совпадают:

V = dEdt = ∂∂Et .

Поэтому, подставляя сюда заданный закон движения, находим компоненты вектора скорости в лагранжевых координатах:

75

1.МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Вэйлеровых координатах вектор скорости в данном случае можно определить двумя способами. В обоих случаях сначала необходимо переписать заданный закон движения в эйлеровых координатах:

В соответствии с первым способом достаточно в полученном ранее поле скоростей заменить лагранжевы координаты на эйлеровы, используя новую запись закона движения

Следует отметить, что такой простой способ может быть применим лишь в тех случаях, когда вид закона движения позволяет легко перейти от лагранжевых координат к эйлеровым и наоборот, как это приведено в рассматриваемой задаче. В более сложных случаях для определения поля скоростей по заданному в эйлеровых координатах закону движения следует применять второй способ, основанный на использовании формулы Б. В. Кучеряева (1.2.95), которую запишем в скалярной форме:

где якобиан JE преобразования эйлеровых координат в лагранжевы вычисляется по формуле (1.2.20).

Далее понадобятся компоненты градиента вектора Ж. Лагранжа

76

1.2. КИНЕМАТИКА

Подстановкой компонент градиента в (1.2.20) определим якобиан преобразования эйлеровых координат в лагранжевы:

e bt

JE = 1 aE1(1 e bt ) .

Далее найдем частные производные лагранжевых координат по времени:

Теперь подстановкой полученных результатов находим поле скоростей в эйлеровых координатах вторым способом:

Отметим, что, несмотря на относительную простоту применения первого способа по сравнению со вторым, последний способ в большинстве случаев оказывается единственно возможным способом решения задач МСС при заданном законе движения в эйлеровых координатах.

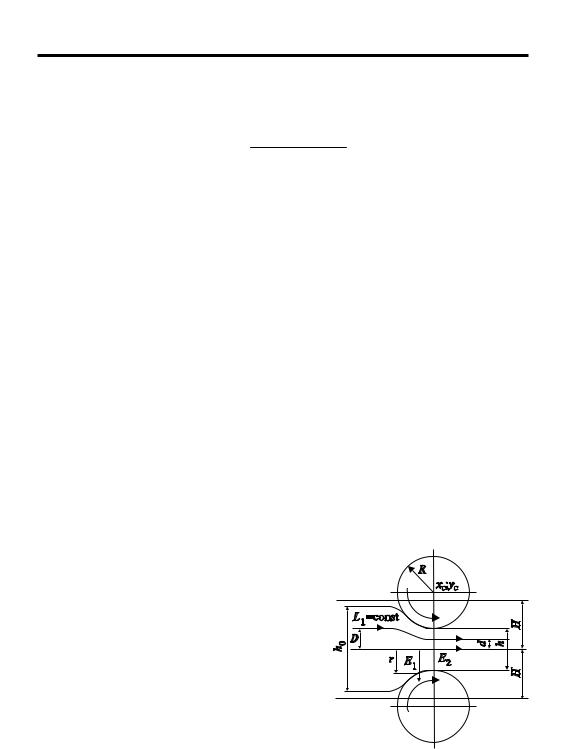
Задача 1.2.6.2. Зависимость лагранжевых линий L1 = const, совпадающих с линиями тока < = const, при стационарном процессе прокатки металла между гладкими валками радиуса R (рис. 18) может быть представлена в виде

c2 E1,

Рис. 18. Расчетная схема прокатки

77

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

соты полосы до прокатки h0 к ее высоте после прокатки h1; Ei – эйлеровы координаты, для которых линия E1 = H совпадает с осью симметрии области деформирования, а линия E2 = 0 пересекает поверхность прокатываемой полосы на

Определить компоненты вектора скорости в очаге деформации при прокатке полосы и построить изотахи (линии равного уровня скоростей) Vi = const.

Решение. По условию задачи лагранжевы изолинии L1 = const совпадают с линиями тока Ψ = const, для которых функция Ψ тока связана с полем скорос-

возмущенного движения; С – несущественная константа. Тогда частные производные L1 по Ei можно представить в виде

∂L1 = V2 ; ∂L1 = − V1 .

∂E1 V0 ∂E2 V0

Действительно, при подстановке последних соотношений в дифференциальное уравнение линий тока (1.2.107) получим dL1 = 0, что соответствует постоянству L1 вдоль линии тока.

Подстановкой заданной функции L1 = L1(Ei) в последние соотношения получим компоненты вектора скорости

78

1.2. КИНЕМАТИКА

Самостоятельно проверить, что полученное поле скоростей является гармо ническим (соленоидальным и потенциальным).

Для построения изолиний Vi = const (изотах) необходимо использовать ал горитм, позволяющий выполнить решение трансцендентного уравнения отно сительно масштабного фактора H = H(R, h0, h1), которое легко осуществить ме тодом касательных (методом И. Ньютона).

На рис. 19 показан пример распечатки результатов расчета. Следует обра тить внимание на характер распределения изотах Vk = const.

Использованное в настоящей задаче гармоническое поле скоростей является однородным лишь в зонах, где либо E2 = –φ (V1 = 0; V2 = V0), либо E2 = φ (V1 = 0; V2 = V0h0/h1), которым соответствует поступательное движение с компонентами тензора скорости дисторции, равными нулю. В остальных частях области движе ния среды это движение является возму щенным (тензор скорости дисторции от личен от нулевого тензора). При этом наибольшее возмущение наблюдается ближе к началу координат (область кон такта деформируемого металла с вращаю щимися валками). В связи с изложенным картины изолиний (рис. 19) получились

как бы «размазанными» по оси E2, а не ло Рис. 19. Изотахи гармонического поля

кализованными в области контакта ме талла с валками, как в реальной картине изотах для процесса прокатки (рис. 20). Кроме того, расчетные изолинии V2 = = const расходятся от поверхности к оси проката (рис. 19), а на реальной картине, наоборот, они расходятся от оси к поверх ности. Однако несмотря на отмеченные недостатки гармонического поля скоро стей, с его помощью можно оценивать некоторые технологические параметры

79

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Задача 1.2.6.3. По заданному в криволинейной полосе стационарному полю скоростей Vj = Vj(E1,E2) движения несжимаемой сплошной среды определить компоненты пространственного градиента деформаций

||V || =V0λ (V1 = 0; V2 =V0λ) , где λ – коэффициент вытяжки.

Решение. Координаты Ж. Лагранжа, так же как и в предыдущей задаче, назначим так, чтобы изолинии L1 = const совпадали с линиями тока (1.2.103):

Далее воспользуемся тем, что для несжимаемых сред якобиан преобразования координат

JE = ∂Lj =1.

∂Ek

Отсюда с учетом значений компонент первой строки получим соотношение для компонент второго столбца

∂L2 V1 + ∂L2 V2 =V0.

∂E1 ∂E2

Подставим полученные результаты в закон сохранения материальных частиц (1.2.10), который в скалярной форме записи имеет вид

80