книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)

1.1. ФОРМАЛИЗАЦИЯ ПОНЯТИЙ

С позиции этих определений сплошной слиток, выдавливаемый из контейнера в единственное отверстие канала мат-

рицы, когда внешнее воздействие на выдавленную часть изделия пренебрежимо мало, является полуслоем (рис. 4, а), а сплошная заготовка, деформируемая меж-

ду двумя вращающимися валками, при аналогичных допущениях является слоем (рис. 4, б).

Объединение слоев M сплошного тела M (1.1.1) называется многослойным телом (рис. 5). Если для многослойного тела существуют сечения, в которых

обозначены области тела окружения и тел включения, то такое тело называется волокнистым (рис. 1). Если тело M состоит из тела окружения, тел включения, слоев и полуслоев, то оно называется армированным.

Принято, что в материальные объекты и их движение на данной стадии исследования нас не интересуют. Поэтому значимые изменения свойств среды в предложено учитывать изменением значимого внешнего воздействия 6. Откликом на это со стороны исследуемой среды M является изменение конечной совокупности ее свойств P. При этом на общей границе SΔΕ тел M и MΕ сплош-

допускается разрыв (скачок) свойств P. В такой среде всегда будем предполагать существование характерного размера, связанного с неоднородностью ее свойств. Например, в волокнистой среде – это значение расстояния между волокнами или размеры самих волокон. Тогда можно назначить некоторый масштаб длины, в пределах которого гетерогенные свойства представляются путем того или иного осреднения их эквивалентными гомогенными свойствами, что приведет к идеализации, основанной на стохастическом описании свойств среды. В таких случаях будем считать, что среда наделена свойствами макроскопической го могенности, а сами свойства называть эффективными в смысле эффективной замены гетерогенных свойств.

1.1.4. Понятие о математической постановке и решении краевых задач

Принятые допущения, гипотезы, определения и их следствия позволяют рассматривать реальный мир как объект математического моделирования. Остав-

21

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

ляя, как оговорено выше, за собой возможность при необходимости расширять конечную совокупность свойств P объекта исследования M, можно создавать модели в идеализированном пространстве, сколь угодно близкие к поведению материи в реальном пространстве и времени.

В ТП в качестве объекта исследования рассматривается сплошная среда M, для которой значимым является термомеханическое внешнее воздействие Σ на границе S и в объеме Ω, приводящее к изменению термомеханических свойств P среды. Под термомеханическим внешним воздействием будем понимать совокупность статического, кинематического и температурного воздействий окружающей среды пространства . Для объекта исследования M на поверхности

S с внешней единичной нормалью n это будут граничные статические, кинема тические и температурные условия соответственно.

Естественно, что вечное движение материи исследователь изучает лишь в определенном временном интервале. Если исследуемая конечная совокупность свойств P материального объекта не претерпевает значимого изменения в рассматриваемом интервале времени, то утверждают, что объект участвует в ста ционарном процессе движения. Для нестационарных процессов значимым является начальное состояние (в начальный момент времени t0 исследования) объекта. Для таких процессов это состояние должно быть задано начальными условиями (начальными при t = t0 значениями всех исследуемых свойств объекта).

На поверхности S исследуемого тела внешнее воздействие Σ задается в виде

граничных условий.

Совокупность начальных и граничных условий называется краевыми услови ями. Определение параметров движения материальных объектов, соответствующих на любой стадии движения t ≥ t0 заданным краевым условиям, является сутью краевой задачи МСС. Задание краевых условий является лишь необходимым, но не достаточным этапом математической постановки краевой задачи. Без этого этапа немыслимо решение самой задачи.

На основании общих законов термомеханического движения сплошных сред в МСС получены основные уравнения, отражающие объективное движение материи. К ним относятся: уравнение движения, уравнение неразрывности среды, уравнения связи параметров среды, уравнение теплопроводности и др. Вместе они должны образовывать замкнутое (полное) множество уравнений, в котором количество уравнений равно количеству неизвестных величин.

Математическая постановка краевых задач МСС состоит в записи замкнутого относительно неизвестных параметров движения сплошной среды множества уравнений и краевых условий для этих параметров, обусловливающих это движение. Результатом реализации математической постановки является реше ние краевой задачи МСС, удовлетворяющее замкнутому множеству уравнений и краевым условиям.

22

1.1. ФОРМАЛИЗАЦИЯ ПОНЯТИЙ

Контрольные вопросы

1.Каковы причины идеализации материального мира и форм существования материи?

2.В чем суть идеализации движения объектов исследования?

3.Что называется материальной частицей, пространственной точкой?

4.Что понимают под окрестностью, малой окрестностью точки?

5.В чем суть свойств открытости и связности окрестности материальной частицы или пространственной точки?

6.Что называется материальным телом, пространственной областью, сплошной средой?

7.Какая часть пространства и почему называется пустым пространством?

8.В чем различие анизотропных и изотропных сред?

9.Чем отличаются гетерогенные и гомогенные тела?

10.Какие сплошные среды называются композитными?

11.В чем принципиальное отличие тел окружения от тел включения?

12.Что называется граничной точкой, чем она отличается от материальной частицы и от пространственной точки?

13.Что называется границей тела?

14.Какова роль определения границы в классификации композитных сред?

15.Какие сплошные тела называются односвязными, многосвязными?

16.Какая граница называется односвязной, многосвязной?

17.Что называют полуслоем, слоем, звездой?

18.Какие композиты называются многослойными, волокнистыми, армированными?

19.В чем состоит принцип замены гетерогенных сред их гомогенными эквивалентами с эффективными свойствами?

20.Какое множество уравнений называется замкнутым (полным)?

21.Что называется начальными, граничными, краевыми условиями?

22.В чем суть краевой задачи МСС?

23.Как осуществляется математическая постановка краевой задачи МСС?

24.Каковы требования к решению краевой задачи МСС?

23

1.МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

1.2.КИНЕМАТИКА

...два тела не могут в физическом мире занимать одно и то же место.

А. С. Пушкин

1.2.1. Основные понятия и определения

Кинематика – раздел МСС, изучающий движение материальных объектов без учета причин, вызывающих это движение.

Внешнее воздействие 6, приложенное к телу M, вызывает движение его материальных частиц m. В общем случае они занимают новые пространственные положения, внутри тела изменяются расстояния между отдельными частицами, что может привести к изменению формы и (или) размеров этого тела.

Всякое механическое движение малой окрестности материальной частицы можно условно разложить на составляющие: поступательное движение самой частицы и искажение (дисторция) ее окрестности. При этом, следуя постулату ньютоновской механики, предполагается неизменность во времени t массы окрестности частицы:

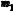
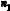
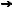
Поступательное движение малой окрестности материальной частицы в некотором множестве координат xi харак- теризуется вектором перемещения

24

1.2. КИНЕМАТИКА

ния n1′ и n2′ пространственных точек, куда попадают эти частицы к моменту времени t в результате движения, обозначим радиус-вектором

и радиус-вектором E + dE = (Ei + dEi )ei соответственно. Здесь dE – то же самое направленное волокно dL тела M, но в произвольный момент времени t.

Тогда перемещение первой частицы

а перемещение второй частицы U + dU = E + dE − L − dL . Отсюда, исключая поступательное перемещение (1.2.4), получим оставшееся приращение перемещения

называемое вектором искажения (дисторции). В соответствии с (П1.83)

где выражение, стоящее в скобках, называется тензором искажения (дистор ции). В общем случае механическое движение малой окрестности материальной частицы (рис. 6, б) можно рассматривать как сочетание отдельных простейших видов движения, к которым относятся поступательное движение (U = 0) и искажение (U ≠ 0) окрестности за счет ее деформации и (или) за счет ее вращения как жесткого тела. Под деформацией окрестности материальной частицы (в дальнейшем – деформацией) понимается всякое изменение в этой окрестности линейных (для волокон) и (или) угловых (для пары волокон) размеров. Применяя (П1.83) к dE и dL в (1.2.5), используя (1.2.6), получим значение тензора искажения:

Однако на практике движение обычно не изучают в отвлеченном по отношению к процессу и к пространству, в котором происходит этот процесс, множестве координат xi. Соотношения (1.2.2) и (1.2.3) можно рассматривать как параметрическое, с помощью xi, задание либо векторной функции

во множестве координат Ж. Лагранжа Li, либо обратной векторной функции

25

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

во множестве координат Л. Эйлера Ei. Движение сплошной среды считается известным, если для любого времени t известна связь между E и L либо в виде (1.2.8), либо в виде (1.2.9). Уравнения (1.2.8) и (1.2.9) называются законом дви жения во множествах координат Ж. Лагранжа и Л. Эйлера соответственно.

Координаты Li информируют о взаимном расположении материальных частиц m в начальный момент времени t0, а сами числа (значения координат) Li являются количественными характеристиками каждой такой частицы в любой момент времени. Эта информация инвариантна во времени. Образно говоря, множество координат Li как бы «вморожено» в движущееся тело M, и каждую изолинию Li = const в сплошной среде в любой момент времени t можно рассматривать как непрерывное упорядоченное геометрическое место материальных частиц, называемое материальным волокном (в дальнейшем – волокном). Каждая материальная частица m M находится на пересечении изоповерхностей Li = const. Поэтому лагранжевы координаты Li обычно называют матери альными координатами. Предполагается, что материальные частицы m в процессе движения не возникают и не исчезают. Поэтому для каждой такой частицы m M справедлив закон сохранения вещества, который с помощью количественных характеристик Li этой частицы записывается аналогично виду закона сохранения массы (1.2.1):

Если в формуле (П1.90) вектор x совпадает с вектором L , то вследствие (1.2.10) полная производная любого тензора по времени в лагранжевых координатах совпадает с частной производной его по времени:

Запись параметров движения сплошной среды в материальном множестве координат Li называется лагранжевым (материальным) описанием движения. Например, с использованием (1.2.8) вектор перемещения (1.2.4) представляется в виде

26

1.2. КИНЕМАТИКА

Дифференциал (П1.83) эйлерового вектора (1.2.8) в лагражевом пространстве

Транспонированный тензор, стоящий в скобках формулы (1.2.12), называется материальным градиентом деформации

Определитель, составленный из компонент матрицы этого тензора, называется якобианом преобразования лагранжевых координат в эйлеровы

Необходимым и достаточным условием существования функции (1.2.9) обратной функции (1.2.8) являются конечность и отличие от нуля якобиана (1.2.14).

Координаты Ei характеризуют пространственное положение материальных частиц в произвольный момент времени. Изолинии, вдоль которых Ei = const, можно рассматривать как непрерывное упорядоченное геометрическое место пространственных точек n, куда попадают материальные частицы m в момент времени t. Каждая пространственная точка n N находится на пересечении изоповерхностей Ei = const. Поэтому эйлеровы координаты обычно называют про странственными координатами.

По определению изменение пространственных координат материальных частиц по времени называется скоростью перемещения частиц (в дальнейшем –

скоростью):

Если в формуле (П1.90) вектор x совпадает с вектором E, то полная производная тензора по времени в эйлеровой системе отсчета состоит из частной производной этого тензора во времени и конвективных слагаемых, обусловленных переносом окрестности материальной частицы со скоростью v (1.2.15):

27

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Запись параметров движения сплошной среды в пространственных координатах Ei называется эйлеровым (пространственным) описанием движения. Например, с использованием (1.2.9) вектор перемещения (1.2.5) представляется в виде

Дифференциал (П1.83) лагранжевого вектора (1.2.9) в эйлеровом пространстве

Транспонированный тензор, стоящий в скобках (1.2.18), называется про

странственным градиентом деформации

Определитель, составленный из компонент матрицы этого тензора, называется якобианом преобразования эйлеровых координат в лагранжевы

Так же, как и (1.2.14), якобиан (1.2.20) должен быть конечным и отличным от нуля. Материальный (1.2.13) и пространственный (1.2.19) градиенты деформации связаны правилом частного дифференцирования:

( L) c( E) = ( E) c( L) ≡ Тδ.

С помощью (1.2.4) тензор искажения (1.2.7) может быть записан в лагранжевом

28

1.2. КИНЕМАТИКА

Теперь уточним понятие стационарного процесса, введенное в пп. 1.1.4. Независимость процесса движения от времени t в лагранжевом и эйлеровом мно-

жествах отсчета имеет различную физическую трактовку. Пусть количествен-

n

ной характеристикой некоторых свойств сплошной среды является тензор Ta .

В любом множестве отсчета процесс изменения этой величины называется стационарным, если

n

∂ Ta = 0 . (1.2.23)

∂t

Для лагранжевых координат из (П1.90) и (1.2.10) следует, что записи (1.2.23)

n

эквивалентна запись ddtTa = 0 . Физический смысл этого состоит в том, что ха-

n

рактеристика свойств Ta окрестности одной и той же частицы m при ее прохождении через различные пространственные точки n не меняется.

Для эйлеровых координат из (1.2.16) следует, что записи (1.2.23) эквивалентна

рактеристика свойств окрестности частицы m полностью определяется координа-

тами Ei пространственных точек n и значением вектора скорости V материальных частиц в этих точках. Иными словами, в фиксированной пространственной точке n для любой материальной частицы m, попадающей в положение n, характеристика свойств не меняется. В частности, для стационарного поля скоростей

Задачи к пп. 1.2.1

Задача 1.2.1.1. По заданному в лагранжевых координатах закону движения (1.2.8)

E = L1e1 + a(L2 L3e2 + L3L1e3 ),

где a – константа с размерностью, обратной размерности единицы длины, определить закон движения в эйлеровых координатах и вектор перемещения в обоих множествах координат.

29

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Решение. Перепишем заданный вектор Л. Эйлера E в скалярной форме:

E1 = L1; E2 = aL2L3; E3 = aL3L1.

Отсюда найдем компоненты вектора Ж. Лагранжа L в эйлеровых координатах:

что позволяет записать в векторной форме закон движения в эйлеровых координатах (1.2.9):

L = E1e + E1E2 e2 + E3 e3 .

E3 aE1

Теперь, учитывая связь вектора перемещения U с векторами Л. Эйлера и

Ж. Лагранжа (1.2.11) U (Li ) = E(Li ) − L , с помощью заданного закона движения определим вектор перемещения в лагранжевых координатах:

U = L2 (aL3 −1)e2 + L3 (aL1 −1)e3 .

Аналогичным способом с помощью полученного в процессе решения закона движения найдем вектор перемещения в эйлеровых координатах (1.2.17):

Задача 1.2.1.2. В координатах Ж. Лагранжа задан вектор перемещения

U = a(L1L22e1 + L2 L23e2 + L3L12e3 ) ,

где а – константа с размерностью, обратной квадрату единицы длины. Определить пространственное положение материальной частицы, первоначально находившейся в пространственной точке n (1, 2, 3) при a = 1.

Решение. Радиус-вектор положения материальной частицы до движения

L = e1 + 2e2 + 3e3 .

30