книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)

1.2. КИНЕМАТИКА

Отсюда видно, что общее изменение длины волокна, так же как это было установлено в предыдущей задаче, связано лишь с изменениями проекций вектора dE на вторую и третью эйлеровы оси координат.

Задача 1.2.3.3. Используя тензоры TC и TE задачи 1.2.3.1, определить главные компоненты тензора конечных деформаций О. Коши и тензора конечных деформаций Л. Эйлера.

Решение. Составим характеристическое уравнение матрицы тензора конечных деформаций О. Коши, полученного в задаче 1.2.3.1: | Cij – λδij| = 0 или

составим диагонализированный вид тензора конечных деформаций О. Коши:

Тогда в соответствии с (2.4) тензор конечных деформаций Л. Эйлера в главных координатах

51

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Эти же результаты можно получить, решая полные кубические характеристические уравнения –λ3 + CIλ2 – CIIλ + CIII = 0 и –λ3 + EIλ2 – EIIλ + EIII = 0, где инварианты тензора конечных деформаций О. Коши

а инварианты тензора конечных деформаций Л. Эйлера

Самостоятельно проанализировать физический смысл компонент тензоров конечных деформаций О. Коши и Л. Эйлера в главных координатах.

1.2.4. Теория малых деформаций

Деформация окрестности материальной частицы называется малой дефор

В этом случае для параметров движения среды нет значимого различия между приращениями эйлеровых и лагранжевых координат, проявляющегося в отличии в общем случае между компонентами тензоров конечной деформации (1.2.42) и (1.2.59). При выполнении условия (1.2.69) эти тензоры с точностью до

величин U U второго порядка малости по сравнению с тензором ис-

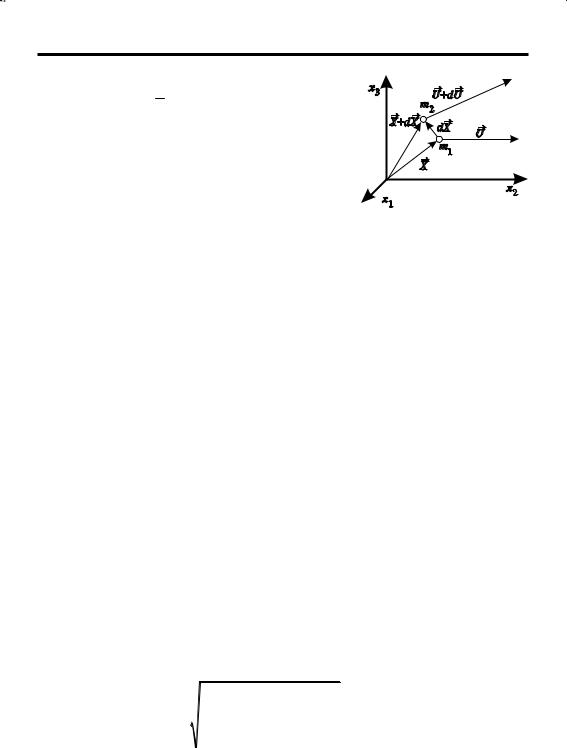
каженияU совпадают. Это позволяет использовать обобщенное безотноси тельное множество координат xi (рис. 13) вместо Li или Ei с оператором У. Р. Гамильтона в виде (П1.74). В отличие от рассмотренных в пп. 1.2.2 и 1.2.3 теорий конечных деформаций, построенная на допущении (1.2.69) теория называется теорией малых деформаций. В рамках этой теории ДС окрестности точки характеризуется тензором малых деформаций (в дальнейшем – просто тензором де формаций)

52

Видно, что симметричная часть тензора искажения точно совпадает с тензо ром малых деформаций (1.2.70). Альтернативная часть TΖ тензора искажения в (1.2.71), называемая тензором жесткого поворота, связана с вращением окрес тности частицы как жесткого тела, что подтверждается соотношением ( U U ) dx ( uU) dx , совпадающим с точностью до символики с тождеством (П1.86) с учетом (П1.84). Значит, симметричная часть тензора ис каженияU характеризует малую деформацию в окрестности материальной частицы, а альтернативная часть – жесткое вращение:

Физический смысл компонент тензора малых деформаций становится яс ным, если их рассматривать как частный случай компонент тензоров (1.2.42) и (1.2.59) при условии (1.2.69). Поэтому диагональные компоненты тензора ма лых деформаций называют линейными деформациями, а боковые компоненты –

сдвиговыми деформациями, или деформациями сдвига.

Из формулы (1.2.33) с помощью (1.2.28), (1.2.40), (1.2.42) в координатах xi

53

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Здесь второе слагаемое под знаком радикала опускается как величина второго порядка малости по сравнению с первым слагаемым. Аналогичный вывод с помощью (1.2.46), (1.2.57) и (1.2.59) при тех же допущениях получается, если использовать формулу (1.2.51):

Видно, что величины (1.2.73), (1.2.74) совпадают с диагональными компонентами (i = k) тензора (1.2.70):

т. е. i-е диагональные компоненты тензора малых деформаций равны относительному изменению длины волокна, параллельного оси xi. Поэтому в технологических расчетах относительную деформацию часто оценивают с помощью линейных деформаций.

Теперь с помощью (1.2.35), (1.2.40) и (1.2.42) перейдем к изучению изменения угла между волокнами, параллельными осям xi и xj (i ≠ j). По аналогии с представлением δi в виде (1.2.73)

Связь боковых компонент тензора (1.2.70) с изменением угловых размеров можно получить из (1.2.53) с помощью (1.2.57) и (1.2.59):

54

1.2. КИНЕМАТИКА

В этом случае сдвиговые деформации νij ≈ – 2εij (i ≠ j). Если сравнивать этот результат с (1.2.77), то при одинаковых по абсолютной величине сдвиговых деформациях (||γij|| = ||νij||) имеем различие в знаках, которое переносится в теорию малых деформаций из материального и пространственного представлений движения. Например, если острый угол между недеформированными волокнами в процессе движения преобразуется в прямой, то поворот волокон происходит в одном направлении. Если же острый угол между волокнами после деформации получается из прямого угла, то поворот осуществляется в обратную сторону. Таким образом, в рассматриваемом случае γij= – νij и абсолютные значения боковых компонент тензора малых деформаций в обоих случаях совпадают.

Тензор малых деформаций поворотом координат можно привести к диагональному виду (П1.61)

где главные деформации εi определяются из (П1.58) и удовлетворяют соотношению (П1.62):

Такой же результат легко получается с помощью (1.2.22) из якобиана (1.2.20)

55

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Отличие знака в этом выражении от знака в (1.2.80) опять переносится в теорию малых деформаций из материального и пространственного представлений движения в теории конечных деформаций.

Из (П1.54) с помощью среднего значения ε0 тензора Tε определяем сферичес

кую часть тензора деформаций

Отсюда ясно, что сферическая часть тензора малых деформаций характеризует

изменение объема. Оставшаяся часть (П1.56), называемая девиатором деформаций

характеризует изменение формы окрестности материальной частицы.

Теперь вектор искажения (1.2.72) можно рассматривать как сумму трех векторов

характеризующих изменение формы, изменение объема и жесткое вращение окрестности материальной частицы соответственно, где Tω называется тензо

ром жесткого поворота.

В связи с тем, что для Sε любое направление осей координат является главным, главные направления Dε совпадают с главными направлениями Tε. Отметим, что первый инвариант (П1.60) любого девиатора (П1.56), в том числе и Dε, равен нулю, а остальные его инварианты в общем случае отличны от нуля:

eI = 0; eII = − 12 еkmekm ; eIII = єijke1ie2je3k.

Известно, что выбор множества осей координат является субъективным фактором. Однако свобода его выбора всегда связана с необходимостью решения поставленной задачи. В некоторых случаях в качестве независимых координат можно назначить компоненты тензора деформации или связанные с ним величины. В частности, в теории малых деформаций удобно применять шестимерное пространство А. А. Ильюшина, в котором параметры движения характеризуются средней деформацией ε0 (1.2.80) и пятью независимыми компонентами eij девиатора Dε деформаций. С помощью замены

56

1.2. КИНЕМАТИКА

для произвольного значения параметра β, не зависящего от времени, характеристики движения представляются скалярной величиной ε0 и пятимерным вектором Г = Гiei . Модуль такого вектора

называется интенсивностью сдвиговых деформаций.

Задачи к пп. 1.2.4

Задача 1.2.4.1. Показать, что полную деформацию, полученную в результате двух последовательных малых деформаций, можно рассматривать как сумму этих деформаций, при этом порядок, в котором происходят оба движения, не влияет на полную деформацию.

Решение. Пусть в результате первого перемещения U

Для второго перемещения U ′ результат первого перемещения является исходным. Поэтому dL′j = dE j и в результате второго перемещения U ′ имеем

Модули компонент градиентов перемещений, в соответствии с определением малых деформаций, должны быть малы по сравнению с единицей. Поэтому в последней записи произведениями компонент градиентов перемещений, как

57

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

малыми более высокого (в сравнении с линейными слагаемыми) порядка, пренебрегаем. Кроме того, не отдавая в этом случае предпочтения ни лагранжевым, ни эйлеровым координатам, заменяем их обобщенными координатами xi . Тогда из последней формулы получаем

или для малых деформаций

Сравнивая последнее выражение с dx′j , устанавливаем, что полная малая деформация в результате перемещения U ′′ равна сумме малых деформаций, получаемых последовательными перемещениями U и U ′ , так как dx′j = dx′′j .

Задача 1.2.4.2. В эйлеровых координатах E1, E2 задан вектор перемещения

где константа a имеет размерность квадрата единицы длины. В области малых деформаций определить компоненты тензора конечных деформаций Л. Эйлера и компоненты тензора малых деформаций.

Решение. Определим компоненты тензора конечных деформаций Л. Эйлера:

58

1.2. КИНЕМАТИКА

В области || dE || >> 1, где деформации малы, можно ввести обобщенные координаты xi. Перемещение в этих координатах

Тогда по кинематической формуле О. Коши (1.2.70)

определим малые деформации

Таким образом, в окрестности рассматриваемой точки модуль максимальной относительной ошибки при замене конечных деформаций Л. Эйлера малыми деформациями не превышает 7%.

59

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Задача 1.2.4.2. В области малых деформаций по заданному полю перемещений

где константа b = 1 имеет размерность квадрата единицы длины, в окрестности точки n(1, 2, 4) определить:

1)составляющие механического движения;

2)девиатор Dε и сферическую часть Sε тензора деформаций Tε;

3)главные компоненты εj тензора деформаций Tε;

4)интенсивность сдвиговых деформаций Г.

Решение. 1. Поступательное движение в заданной точке характеризуется вектором перемещения

U = 0,2e1 + 0,4e2 + 0,75e3.

Жесткий поворот окрестности материальной частицы в заданной точке от-

2. Для определения сферической части Sε тензора малых деформаций Tε сначала найдем объемную деформацию ε = εikδik = ε11 + ε22 + ε33 = 0,1875. Тогда сферическая часть тензора малых деформаций (1.2.83)

60