
книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)
..pdf
1.2. КИНЕМАТИКА
то при однородной деформации образца сжатием или растяжением с постоянной скоростью деформации во всем образце (ξ1 = ξ*) получим экспоненциальную зависимость функции f(t) от времени t (1.2.168).
Для расчета степени деформации сдвига Λ по формуле (1.2.162) необходимо определить интенсивность сдвиговых скоростей деформаций Н. При плоской деформации сплошной несжимаемой среды Н вычисляется по формуле задачи 1.2.7.6, и с учетом отсутствия в рассматриваемых процессах сдвигов имеем Н = 2ξ1. Тогда для плоской деформации получаем
tκ
Λ = 2∫ξ1dt.
t0
При нагружении образца в режиме с постоянной скоростью деформирования находим
ξ = ± |
V |
. |
|
h ±tV |
|||
1 |
|
||
|
0 |
|
После подстановки этого значения в предыдущую формулу имеем
tκ |
V dt |
|
|
h ±t V |
|
Λ = ±2∫ |
|
|
= 2ln |
0 κ |
, |
h ±tV |
|
h |
|||
t |
|
|
|
||
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
где учтено, что t0 = 0. Для определения времени окончания процесса нагружения tк воспользуемся граничным условием f(tк) = 1 для функции f(t). Тогда
tκ = V h .
Используя это значение, получаем степень деформации сдвига Λ при однородной деформации образца из несжимаемого материала в режиме с постоянной скоростью деформирования соответственно для растяжения и сжатия:
Λ = 2ln |
h0 + h |
; Λ = 2ln |
|
h0 |
|
h |
h |
− h |
|||
|
|
||||
0 |
|
0 |
|
||
с учетом неотрицательности Λ.
При нагружении образца в режиме с постоянной скоростью деформации (ξ1 = ξ* = const) имеем
101

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД
tк
Λ = 2∫ξ dt =2ξ tк.
t0
В этом случае для определения tк необходимо использовать граничное условие f(tк) = 1 для функции f(t):
t |
к |
= ± |
2 |
ln |
h0 + h |
. |
ξ |
|
|||||
|
|
|
h |
|||
|
|
|
|
0 |
|
|
При подстановке этой величины в предыдущую формулу с учетом неотрицательности Λ получаем значение степени деформации сдвига при однородной деформации образца из несжимаемого материала в режиме с постоянной скоростью деформации соответственно для растяжения и сжатия, точно совпадающее с таковым при однородной деформации образца из несжимаемого материала в режиме с постоянной скоростью деформирования.
Самостоятельно. Показать, что при однородной деформации образцов из несжимаемых материалов в процессах трехмерного сжатия – растяжения пря-
моугольного параллелепипеда с исходными размерами h0, b0,  0 и текущими раз-
0 и текущими раз-
мерами h, b,  (h0b0
(h0b0 0 = hb
0 = hb ; b0 / b =
; b0 / b =  0 /
0 /  ) и при осесимметричном сжатии – растяжении круглого цилиндра с исходными размерами h0, R0 и текущими размерами h, R (h0 R02 = hR2 ) степень деформации сдвига имеет вид
) и при осесимметричном сжатии – растяжении круглого цилиндра с исходными размерами h0, R0 и текущими размерами h, R (h0 R02 = hR2 ) степень деформации сдвига имеет вид
Λ = |
3 ln |
h0 + h |
; Λ = 3 ln |
h0 |
|
h |
h − h |
||||
|
|
|
|||
|
0 |
|
0 |
||
для растяжения и сжатия соответственно.
Указание к самостоятельному решению. Для растяжения–сжатия прямоугольного параллелепипеда (при условиях h0b0 0 = hb
0 = hb ; b0 / b =
; b0 / b =  0 /
0 /  ) можно использовать поле скоростей с компонентами (1.2.113):
) можно использовать поле скоростей с компонентами (1.2.113):
V1 |
= ± |
hE1 |
′ |
= |
hE2 |
′ |
= |
hE3 |
′ |
h |
f ; V2 |
h |
f ; V3 |
h |
f , |
||||
|
|
|
|
|
|
|
а для растяжения–сжатия круглого цилиндра (при условии h0 R02 = hR2 ) можно использовать поле скоростей с компонентами
102

1.2. КИНЕМАТИКА
|
hEz |
′ |
|
|
hEρ |
|
V = ± |
|
f ; |
Vρ |
= |
|
′ |
|
|
|||||
z |
h |
|
|
h |
f ; Vϕ = 0. |
|
|
|
|
|
|
В обоих случаях текущая высота h определяется формулой (1.2.117).
1.2.8. Кинематические граничные условия
При постановке задач ОМД граничные, в том числе и кинематические граничные условия назначаются на основе априорных или апостериорных представлений об изучаемом процессе. Наиболее часто кинематические граничные условия задаются в виде значений вектора скорости (вектора перемещения) или его отдельных компонент на границе области исследования. Очевидно, это связано с ограниченностью нашего восприятия движения материальных объектов. Действительно, трудно, например, предположить значение какой-либо компоненты тензора скоростей деформаций на контакте деформируемого металла с абсолютно жестким инструментом. И совершенно очевидно, что нормальная к поверхности такого инструмента составляющая вектора скорости металла в точке контакта его с инструментом должна быть равна такой же составляющей вектора скорости инструмента в этой же точке. В дальнейшем (пп. 1.5.3) мы будем различать несколько типов граничных условий. Здесь отметим, что с кинематическими параметрами связаны кинематические и смешанные граничные условия.
Кинематические условия в скоростях на границе SV с единичной внешней нормалью
n = niei |
(1.2.169) |
считаются заданными, если на этой границе известен вектор скорости V n , значение, которого должен принимать вектор скоростиV движения среды во всех
граничных точках s:
V =V n s Sv . |
(1.2.170) |
При задании смешанных граничных условий используется либо нормальная
V p , либо касательная V τ к поверхности S составляющая вектора скорости. В первом случае используется заданное значение V p по нормали n к поверхности Sτv, которое должна принимать проекция вектора скорости V движения среды на направление этой нормали:
103
1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД
V Tn |
V p s SΩv , |
(1.2.171) |
|
где в соответствии с (П1.40) |
|
|
|
k |
n ... n. |
(1.2.172) |
|
Tn |
|||
|
|||
Во втором случае используется заданное значение V Ω |
по касательной к по- |
||
верхности Spv, которое должна принимать проекция вектора скорости V на плоскость, касательную к поверхности S в рассматриваемой ее точке s.
Прежде чем записать кинематическую часть граничного условия для второго случая, выполним в общем виде проектирование произвольного вектора a
на плоскость с нормалью n.
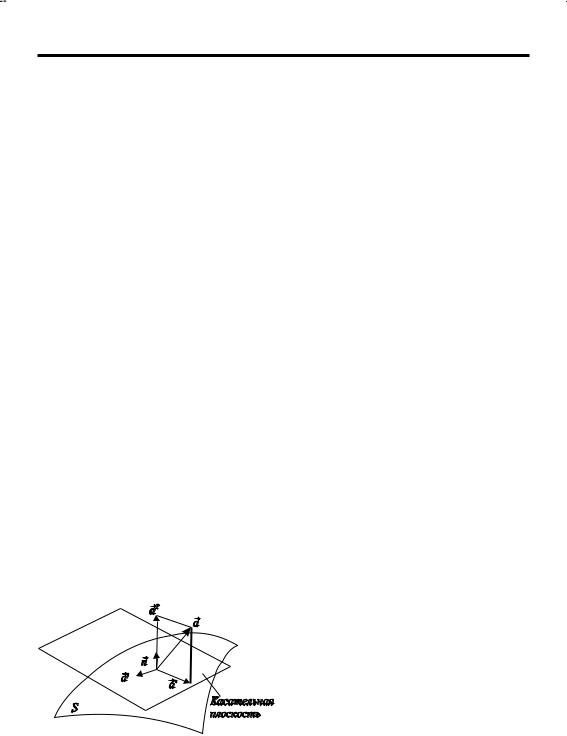
Проектирование вектора a на касательную плоскость поверхности S с нормалью n выполняется в два этапа. На первом этапе находим вспомогательный
вектор (рис. 23) |
|
aχ a υn. |
(1.2.173) |
Упражнение 1.2.19. Доказать, что вспомогательный вектор (1.2.173) лежит в плоскости, касательной к поверхности S с нормалью n, перпендикулярен вектору a и нормали n, а по модулю совпадает с проекцией aΩ вектора a на касательную плоскость.
Для второго этапа проектирования необходимо выполнить следующее упражнение.
Упражнение 1.2.20. Доказать, что векторное произведение единичной внешней нормали n, поверхности S на вспомогательный вектор (1.2.173) точно совпа-
на касательную плоскость этой поверхности:
Рис. 23. Схема к проектированию вектора на плоскость
aΩ n υ a υ n. |
(1.2.174) |
С помощью выполненного проектирования кинематическая часть граничного условия на поверхности Spv записывается в следующем виде:
n υV υ n V Ω s Spv . (1.2.175)
Итак, в дальнейшем будем ссылаться на три типа граничных условий
104

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД |
|
|
|
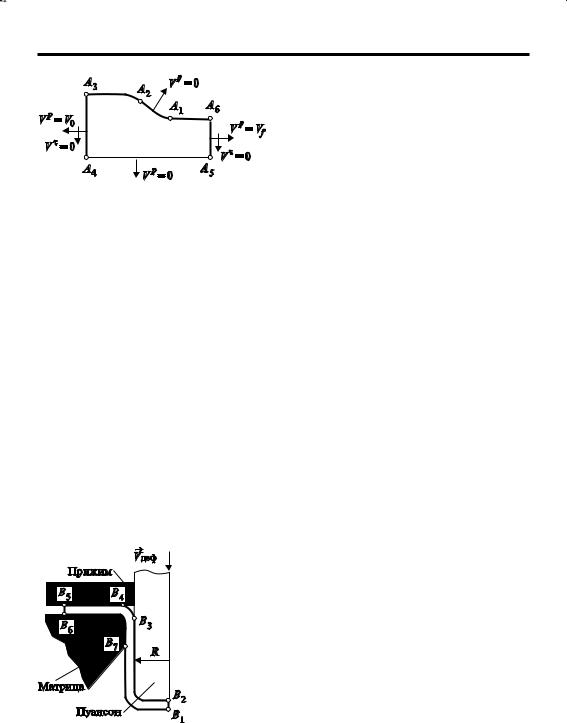
Кроме того, на участках A3A4 и A5A6, |
|
|
где полоса движется поступательно в на- |
|
|
правлении прокатки, касательные со- |
|
|
ставляющие вектора скорости материа- |
|
|
ла полосы V Ω = 0. |
|
|
Участок A4A5 является осью симмет- |
|
Рис. 25. Кинематические граничные условия |
рии, на котором всегда Vp = 0. |
|
Для математической постановки кра- |
||
плоской прокатки |
||
|
евой задачи на всей границе области ме- |
|
ханические (кинематические и (или) статические) граничные условия должны |
||
быть заданы как по нормали к границе, так и по касательной к ней. Из изло- |
||
женного следует, что здесь можно записать лишь часть граничных условий, а |
||
именно – кинематические для поля скоростей V внутри объема деформируе- |
||
мого материала полосы (рис. 24): |
|
|
|
V Tn |
0 s А1А2; |
V Tn |
V0 , n υV υn 0 s A3A4; |
|
|
V Tn |
0 s A4A5; |
V Tn |
Vf , n υV υn 0 s A5A6. |
|
Эти формализованные кинематические граничные условия изображены графически на рис. 25.
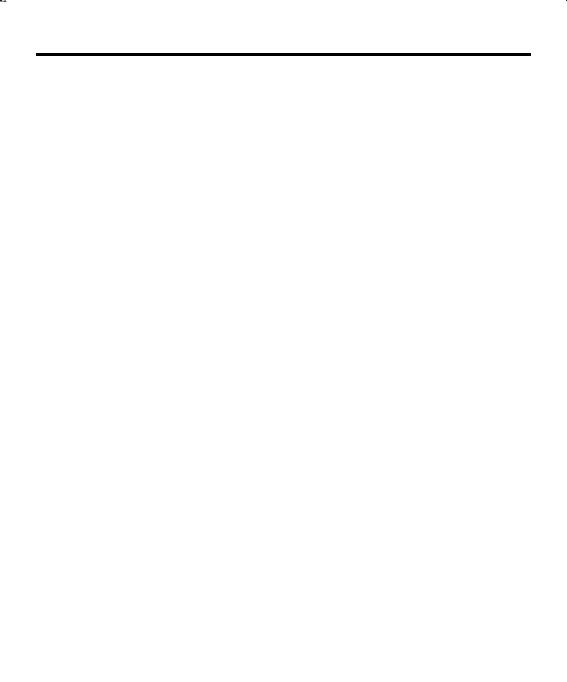
Рис. 26. Кинематические гра9 ничные условия штамповочной операции вытяжки
Задача 1.2.8.2. Записать кинематические граничные условия при вытяжке (операция листовой штамповки) круглой заготовки радиусом Rзаг и толщиной h через матрицу с прижимом в стакан пуансоном радиусом R, если пуансон движется с постоянной скоростьюVɞɟɮ (рис. 26). Предполагается, что толщина листовой заготовки и стенки стакана одинаковы, а материал листовой заготовки несжимаем. Материал всего инструмента (пуансона, матрицы и прижима) считается абсолютно жестким.
Решение. Так же, как и в предыдущей задаче, на границе области течения среды точками Bi выделим участки с одинаковыми граничными условиями. Про-
106

1.2. КИНЕМАТИКА
цесс – осесимметричный, поэтому на рис. 26 изображено сечение только левой половины и используется принцип симметрии.
Участок B1B2 является частью оси симметрии, и здесь нормальная составляющая вектора скорости Vp = 0. Такое же значение этой составляющей следует принять на участках B2B3, B4B5, B6B7 вследствие абсолютной жесткости материала инструмента.
Так как по условию задачи стенка стакана не вытягивается, то на участке B2B3 касательная к поверхности инструмента составляющая вектора скоростиV τ изменяется от Vдеф в точке B3 до нуля в точке B2 и зависит от угла между направлением вектора Vдеф и нормалью n к внутренней поверхности стакана.
Касательная к поверхности инструмента составляющая вектора скоростиV τ на участках B4B5 и B6B7 и нормальная его составляющая Vp на участке B5B6 – одинаковы. Для определенияV τ и Vp запишем равенство потоков деформируемого материала, связанное с его несжимаемостью. С одной стороны, этот поток
равен πVдеф [(R + h)2 – R2], а с другой – 2V τπRзагh . Из равенства этих потоков имеем
V τ =Vдеф 2R + h .
2Rдеф
Касательная к поверхности составляющая вектора скоростиV τ на участке
B5B6 V τ = 0.
Теперь для поля скоростей V внутри деформируемого тела можно в формализованном виде записать все кинематические граничные условия:
V n = 0 s B1B2;
V n = 0, n ×V ×n =Vдеф sinα s B2B3;
V n = 0, n ×V ×n =V |
2R + h |
s B B ; |
|
|||
|
|
|
деф |
2R |
4 5 |
|
|
|
|
|
деф |
|
|
V n = |
||V || 2R + h |
; n ×V ×n = 0 s B B |
; |
|||
|
деф |
2Rдеф |
|
|
5 6 |
|
|
|
|
|
|
|
|
107
1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД
V n = 0, n ×V ×n =V |
2R + h |
s B |
B . |
деф |
2R |
6 |
7 |
|
деф |
|
|
Самостоятельно дать графическую интерпретацию приведенным кинематическим граничным условиям на схеме рис. 26.
1.2.9. Кинематика сплошных композитных сред
Если гетерогенная среда может быть заменена в рассматриваемой области ее движения другой, эквивалентной средой с эффективными гомогенными свойствами, то для описания кинематических параметров движения такой среды могут быть использованы все кинематические зависимости предыдущих пунктов. Естественно, что при таком подходе к описанию движения композитной среды исчезает индивидуальность поведения каждой ее составляющей.
Многообразие вариантов, используемых на практике КМ, является причиной того, что до настоящего времени не разработан метод, позволяющий в самом общем виде осуществить точную реализацию постановки задач о совместном пластическом деформировании разнородных материалов с учетом их взаимодействия в объеме КМ. Однако имеется ряд приближенных методов, позволяющих с необходимой для практических расчетов точностью учитывать особенности деформирования КМ. К ним, в частности, относится упомянутый выше метод осреднения свойств среды, который может быть полезен при инженерной оценке параметров (например, энергосиловых) движения среды с осредненными характеристиками. Другой приближенный метод, рассматриваемый в следующем пункте, позволяет подходить к описанию движения сплошных КМ с учетом индивидуальности их компонент. По существу, он сводится к методу построения искомой функции с помощью основного решения и его последующей корректировки (п. П3).
Проблемы построения основного решения для различных процессов ОМД будут рассмотрены ниже. Здесь, считая основное решение известным, изложим методы построения скорректированных параметров движения КМ, позволяющих учитывать кинематическое взаимодействие всех тел Mα КМ (1.1.1).
Кинематические параметры основного решения будем обозначать строчными буквами: vi; v; ; ui; u; ξik; ψ и т. п., а соответствующие кинематические параметры скорректированного решения – прописными буквами: Vi; V ; Ui; U ; Ξik; Ψ и т. п. Изложение метода построения кинематических параметров движения КМ начнем с кинематики стационарного послойного течения двухслойной среды в условиях двухмерной деформации как одного из наиболее простых вари-
108
1.2. КИНЕМАТИКА
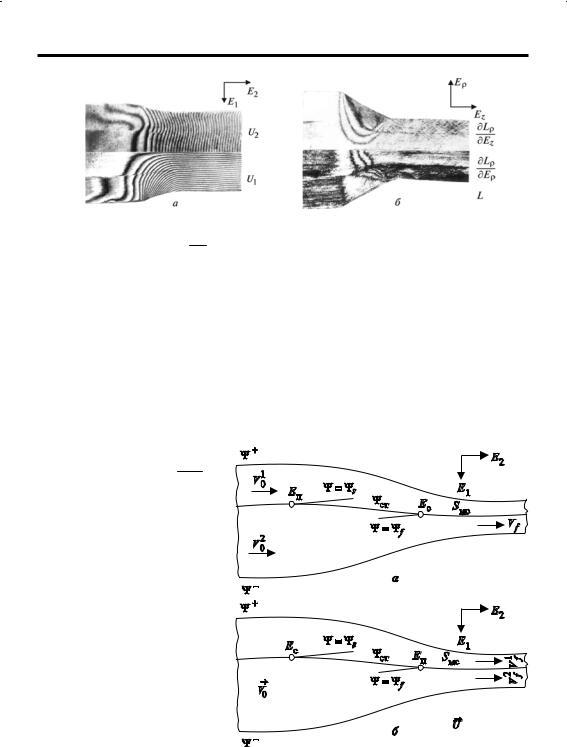
Рис. 27. Муаровые картинки изотет (Uk = const) поля перемещений при прокатке (а) и изолиний поля
пространственного градиента ωLΥ = const при прессовании (б)
ωEz
антов деформирования КМ, основные идеи математического описания кото рого будут распространены на более сложные случаи.
1.2.10. Двухмерное стационарное течение двухслойной среды
Экспериментальные исследования, выполненные с использованием метода муаровых полос (рис. 27), показывают, что на межслойной границе допускается относительное проскальзывание (скачок перемещения, скорости) слоев, а при определенных условиях – их сцепление (выравнивание этих характеристик). В частности, это показано на рис. 27, а распределением изотет (изолиний Ui = const) при прокатке и на
ωLΥ |
|
рис. 27, б – изолиний ωEz = |
|
= const при осесимметрич |
|
ном прессовании прутка. |
|
Исходя из этого явления, |
|
на границе Sмс слоев назна |
|
чим две точки E 2 = E п и |
|
E2 = Eс (рис. 28, а), в которых |
|
заканчивается однородное |
|
течение хотя бы одного из |
|
слоев и начинается сцепле |
|
ние (выравнивание скорос |
|
тей) слоев соответственно |
|
(схема П–С). Однородное те |
|
чение слоев с разными скоро |
|
стямиV01 иV02 до точки Eп и |
|
совместное течение с одина |
Рис. 28. Взаимодействие слоев по схемам П–С (а) и С–П (б) |
|
109

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД
ковой скоростьюV после точки Eс, а также неизменность граничных линий тока ψ = ψ+ и ψ = ψ– можно обеспечить, если в i-х слоях использовать нижеследующие функции тока
Ψ |
1 |
= ψ + b |
(ψ – ψ+)B ; Ψ |
2 |
= ψ + b (ψ – ψ–)B |
c |
(1.2.176) |
|
1 |
c |
2 |
|
с функциями сцепления слоев Bc, созданных по типу склеивающих функций (П3.61)
Bс = 0,5 + 0,0625 (9 sinEт + sin3Eт), |
(1.2.177) |
|||
где |
|
|
|
|
E |
|
= |
π(2E2 − Eп − Ес) . |
|
|
т |
|
2(Еп − Ес) |
|
|
|
|
|
|
Коэффициенты bi в (1.2.176) полностью определяются значениями на стыке слоев у входа в зону возмущенного движения до точки Eп (ψ = ψs) и от точки Eс до выхода из этой зоны (ψ = ψf):
|
ψ |
f |
−ψ |
s |
|
|
|
|
(ψ |
f |
−ψ+ )b |
|
|
|
b = |
|
|
; b |
= |
|
|
|
1 |
|
; |
(1.2.178) |
|||
ψ |
|
|
|
ψ |
|
−ψ− +(ψ+ −ψ− )b B |
||||||||
1 |
s |
−ψ+ 2 |
|
f |
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
c |
|
|
||
Зная функции тока Ψi (1.2.176) в каждом из слоев, по формуле (1.2.105) определим соответствующие компоненты вектора скорости в первом V1 =Vi1ei и
во втором V 2 =Vi |
2ei слоях: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
V11 = v1 (1+ b1Bc ) +b1 (ψ −ψ+ ) |
∂Bc |
; V21 = v2 (1+ b1Bc ); |
|
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂E2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂b |
|
|
|
|
|
∂B |
|
|
|
|
|
|||
V12 = v1 (1+b1Bc ) + (ψ −ψ+ ) |
2 |
Bc +b2 |
c |
|
; V22 = v2 |
(1+ b1Bc ), (1.2.179) |
||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
∂E2 |
|
|
|
|
|
∂E2 |
|
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂b |
|
|
|
ψ+ |
∂B |
|
∂B |
|
|
0, 0625π |
|
|
|
|
|||||||
|
2 |
= − |
|
|
|
b2 |
c |
; |
|
|
|
c |
= |
|
|
|
|
(9 cos E |
|
+3cos 3Е |
). |
|
|
∂E |
|
ψ |
f |
−ψ+ 2 |
∂E |
|
∂E |
2 |
|
|
Е |
п |
− Е |
с |
|
т |
т |
|
|||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
110
