
книги / Методы вычислительной математики
..pdf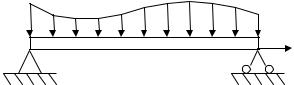
9. ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В отличие от задачи Коши, в граничных задачах условия для определения постоянных интегрирования задаются в нескольких различных точках отрезка, на котором строится решение дифференциальной задачи. В качестве примера рассматривается ряд постановок таких задач.
Механическое движение точки вдоль прямой описывается уравнением mxtt′′ = Fx (t, x, xt′),
причем известно, что к моменту времени Т точка должна пройти расстояние L. Требуется найти закон движения точки. Очевидно, что условия для нахождения постоянных интегрирования в рассматриваемом случае заданы для разных моментов времени и могут быть записаны так: x(0) = 0, x(T) = L.
Неподвижная горизонтальная балка закреплена на опорах и испытывает действие распределенной по ее длине перерезывающей нагрузки (рис. 9.1). Уравнение изгиба
балки записывается в форме
EIw′xx′ = −M (x),
где Е – модуль упругости материала, I – момент инерции поперечного сечения балки, w(x) – функция, описывающая прогиб балки, М(х) – переменный из-
гибающий момент от действия поперечной нагрузки q(x). Шарнирные закрепления балки на опорах означают, что прогибы в крайних точках равны нулю: w(0) = 0, w(L) = 0.
Температурное поле θ(x) в стержне, теплоизолированном с боковой поверхности, описывается уравнением одномерной теплопроводности:
λθ′xx′ + J (x,θ)= 0 ,
где λ – коэффициент теплопроводности, J(x, θ) – мощность внутренних тепловых источников. Предполагается, что на левом торце стержня поддерживается постоянная температура θ(0) = θ0 (граничное условие первого рода), а на пра-
вом – |
происходит теплообмен |
с окружающей средой, имеющей температу- |
||||||||||||
ру θ |
|
, то есть выполняется граничное условие |
λθ |
x ( |
L |
) |
|
( |
L |
) |
− θ |
|
|
|
|
|
|
= −α θ |
|
|
|
(гра- |
|||||||
|
cp |
|
|
′ |
|
|
|
|
|
|
|
cp |
|
|
ничное условие второго рода), |
где α – коэффициент теплоотдачи с торцевой |
|||||||||||||
191
поверхности стрежня в окружающую среду. Иначе последнее условие может быть записано в виде смешанного граничного условия αθ(L)+ λθ′x (L)=αθcp (граничное условие третьего рода).
Поскольку обыкновенное дифференциальное уравнение порядка n можно представить в виде системы n обыкновенных дифференциальных уравнений первого порядка, в общем случае постановка граничной задачи выглядит следующим образом: определить дифференцируемые функции uk (x), удовлетво-
ряющие дифференциальным уравнениям
uk′,x (x) = fk (x,u1(x),u2 (x),…,un (x)), k = |
|
(9.1) |
1, n |
на отрезке [a, b], причем условия накладываются на функции uk (x) более чем в одной точке этого отрезка,
ϕk (u1 (xk ),u2 (xk ),…,un (xk ))= 0, xk [a,b], k = |
|
. |
(9.2) |
1,n |
9.1. Метод пристрелки
Требуется отыскать решение системы двух обыкновенных дифференци-
альных уравнений |
|
|
|
|
|
|
|
u1,′x (x) = f1(x,u1(x),u2 (x)), |
|
||||||
|
|
|
|
|
|
|
(9.3) |
|
(x) = |
f2 (x,u1(x),u2 (x)) |
|||||
u2,′ x |
|
||||||
|
|
|
|
|
|
|
|
с граничными условиями |
|
|
|
|
|
|
|
ϕ1 (u1 (a),u2 (a))= 0, |
|
||||||
|
|
|
|
|
|
|
(9.4) |
|
|
|
(u |
(b),u |
|
(b)) = 0. |
|
ϕ |
2 |
2 |
|
||||
|
|
1 |
|
|
|
||
Значение первой искомой функции u1 в левой точке отрезка [a,b] полага- |
|||
ется равным произвольно заданному числу D, то есть u1 (a) = D. Тогда из перво- |
|||
го граничного условия, ϕ1 (D, u2 (a)) = 0, как из уравнения, можно определить |
|||
значение второй искомой функции в точке а, u2 (a; D). Теперь значения |
|
||
u1 (a) = D, |
|
||
|
|
|
(9.5) |
|
|
(a; D) |
|
u |
2 |
|
|
|
|
|
|
можно рассматривать как начальные условия для системы дифференциальных уравнений (9.3), то есть вместо граничной задачи сформулирована задача Коши. Решая каким-либо известным способом задачу (9.3) с начальными условиями (9.5), можно найти решения u1 (x; D) и u2 (x; D) как функции парамет-
ра D. Однако при подстановке этих решений во второе граничное условие (9.4)
192
в общем случае не будет получено тождество из-за произвольного выбора па-
|
~ |
раметра D. С другой стороны, можно попытаться подобрать такое значение D |
|
~ |
~ |
(а соответственно, функции u1 (x; D) и u2 |
(x; D)), при котором это выражение бу- |
дет обращаться в тождество |
|
~ |
~ |
ϕ2 (u1 (b; D), u2 (b; D))= 0. |
|
В случае, когда последнее выражение является достаточно сложным, его |
|
можно рассматривать как нелинейное уравнение относительно параметра D
~
и использовать для определения D любой из известных методов поиска корня нелинейного уравнения.
Пример 9.1. Решить задачу теплопроводности для однородного тонкого стержня с теплоизолированной боковой поверхностью:
λθ′xx′ + J (x,θ)= 0
при λ = const, J = const и граничных условиях
αθ(0)λθ′x (0) = αθcp , θ(1) = θ1.
Вводятся обозначения
u1 = θ, u2 = θ′x ,
которые позволяют представить исходное уравнение в виде системы двух обыкновенных дифференциальных уравнений:
u1′, x (x) = u2 (x),
u2′, x (x) = −J / λ
с граничными условиями
αu (0)− λu |
2 |
(0)=αθcp , |
|
|
1 |
|
|
|
(1)= θ1. |
|
|
u |
|
|
|
1 |
|
|
|
В соответствии с идеей метода пристрелки значение первой искомой |
|||
функции u1 в левой точке принимается равным u1 (0) = D . Из первого гранично- |
|||
го условия, как из уравнения, |
вычисляется значение |
|
второй искомой функ- |
|||||||||
ции u2 в той же точке, |
|
) |
1 ( |
|
) |
|
( |
|
) |
|
||
u |
2 ( |
0 |
0 |
D − θcp |
/ λ, |
|||||||
|
|
= α u |
|
|
− θcp / λ = α |
|
|
|||||
что позволяет перейти к задаче Коши,
193
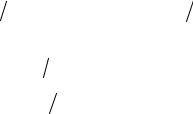
u1,′x (x)= u2 (x), |
u1 (0) = D, |
|||
|
|
|
|
|
|
λ; |
|
|
(0)= α(D − θср ) λ. |
u2,′ x (x)= −J |
u |
2 |
||
|
|
|
|
|
Интегрирование этой системы дает решение
u2 (x)= −Jx |
λ + C1, |
|
|
||
|
|
|
|
|
|
|
|
(x)= −Jx2 |
2λ + C x + C |
. |
|
u |
|||||
|
1 |
|
1 |
2 |
|
Использование начальных условий
u1 (0) = D, u2 (0)= α(D − θср )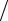 λ
λ
позволяет определить постоянные интегрирования
C1 = α(D − θcp )/ λ, C2 = D.
и записать решение задачи в виде
u (x) = −Jx / λ + α(D − θcp )/ λ,
2
u1 (x) = −Jx2 |
/ 2λ + α(D − θcp )/ λ + D. |
|
|
Подстановка полученного решения во второе граничное условие u1 (1)= θ1 дает выражение
u1 (1)= −J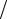 2λ + α(D − θср )
2λ + α(D − θср )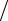 λ + D = θ1
λ + D = θ1
которое можно рассматривать как уравнение относительно произвольного параметра D, что позволяет определить неизвестную величину
D = (J + 2λθ1 + 2αθcp )/ 2(α + λ). |
|
|
|
||
Окончательно решение исходной задачи принимает вид |
|
|
|||
θ(x) = −Jx2 / 2λ + α J + 2λ(θ1 |
− θcp ) x / 2λ(α + λ) + J + 2 |
(λθ1 |
+ αθcp ) / 2 |
(α + λ). |
|
|
|
|
|
|
|
9.2. Метод дифференциальной прогонки
Рассматривается система n обыкновенных дифференциальных уравнений
{u′x (x)}+ [A(x)]{u(x)}= {f (x)} |
(9.6) |
||
с граничными условиями |
|
||
[ϕk ]{u(xk )}={αk }, k = |
|
. |
(9.7) |
1,m |
|||
Пусть в точке x1 задано p1 граничных условий, в точке x2 – p2 граничных условий, и так далее. Общее число граничных условий равно числу дифферен-
m
циальных уравнений системы (9.6), то есть ∑ pk = n . Например, для системы
k=1
двух дифференциальных уравнений задача (9.6)–(9.7) представляется в форме
194
u1,′ x (x)+ a11(x)u1(x)+ a12 (x)u2 (x) |
= f1(x), |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x)+ a22 (x)u2 (x) |
= f2 (x), |
|||||||
u2,′ x (x)+ a21(x)u1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ11u1 (x1 ) |
+ ϕ12u2 (x1 )= α1, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u (x |
|
) + ϕ |
|
u |
|
(x |
|
)= α |
|
. |
||
ϕ |
2 |
22 |
2 |
2 |
2 |
||||||||
|
21 |
1 |
|
|
|
|
|
|
|||||
Соответствующие матрицы в выражениях (9.6) и (9.7) принимают вид
u (x)
{u(x)}= 1 ( ) ,
u x2
[ϕ1 ]=  ϕ11 ϕ12
ϕ11 ϕ12  ,
,
a (x) a (x)
[A(x)]= 11 12 ,
a21(x) a22 (x)
{α1}= α1 , [ϕ2 ]=  ϕ21
ϕ21
f1 |
(x) |
, |
|
{f (x)}= |
|
|
|
f |
2 |
(x) |
|
|
|
|
|
ϕ22  , {α2 }= α2 .
, {α2 }= α2 .
Основная идея метода дифференциальной прогонки заключается в сведении граничной задачи (9.6), (9.7) к задаче Коши, то есть в сведении граничных условий (9.7), заданных для m разных значений аргумента, к n условиям, заданным для одного значения аргумента. Рассматривается вспомогательное функциональное соотношение
[v(x)]T {u(x)}= {γ(x)},
где
v11 (x)v (x)
[v(x)]T = 12
v1n (x)
v21 (x) |
vn1 |
(x) |
|||
v22 (x) |
|
|
|
||
vn2 |
(x) |
||||
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
(x) |
|
|
|
v |
2n |
v |
nn |
(x) |
|
|
|
|
|
||
(9.8)
γ1 |
(x) |
|
|
|
|
γ |
(x) |
|
{γ(x)}= |
2 |
. |
|
|
|
|
|
|
γ |
(x) |
|
|
n |
|
Если предположить, что функциональные матрица [v(x)] и вектор {γ(x)} известны, выражение (9.8) для заданного x = b представляет собой систему алгебраических уравнений
[v(b)]T {u(b)}= {γ(b)} |
(9.9) |
относительно значений u1 (b), u2 (b), …, un (b), которые теперь можно использо-
вать как начальные условия для системы обыкновенных дифференциальных уравнений (9.6).
Выражение (9.8) дифференцируется в предположении, что [v(x)] и {γ(x)} – достаточно гладкие (дифференцируемые) функции,
[v′(x)]T {u(x)}+ [v(x)]T {u′x (x)}= {γ′(x)}.
195

С учетом исходной системы уравнений (9.6) из приведенного соотношения получается
[v′(x)]T {u(x)}+ [v(x)]T ({f (x)}− [A(x)]{u(x)}) ={γ′(x)}, ([v′(x)]T − [v(x)]T [A(x)]){u(x)}={γ′(x)}− [v(x)]T {f (x)}.
Последнее выражение будет справедливо для любых функций {u(x)}, например, при выполнении условий
[v′x (x)]T − [v(x)]T [A(x)]= 0, {γ′x (x)}− [v(x)]T {f (x)}= 0.
Отсюда получается система n × n + n обыкновенных дифференциальных
уравнений относительно [v(x)] и {γ(x)}, |
|
[v′x (x)]− [A(x)]T [v(x)]= 0, |
(9.10) |
{γ′x (x)}− [v(x)]T {f (x)}= 0. |
(9.11) |
В соответствии с выражением (9.7) в первой точке |
x1 = a заданы p1 гра- |
ничных условий. В (9.10) и (9.11) выбираются подходящие дифференциальные уравнения (таких уравнений будет p1 × p1 + p1 ), для которых с помощью этих
граничных условий можно определить начальные условия, и интегрируются на отрезке [x1, x2]. Это позволит определить значения выбранных функций [v(x)] и {γ(x)} в следующей точке x2. Но в этой точке заданы еще p2 граничных условий исходной задачи, что, в свою очередь, позволяет выбрать еще p2 × p2 + p2
дифференциальных уравнений из систем (9.10), (9.11) и проинтегрировать их вместе с первым набором уравнений на втором участке. Последовательно выполняя эту процедуру для всех отрезков [xk , xk+1 ], k =1,m −1, в конечном итоге
можно получить значения всех функций [v(xm)] и {γ(xm)} для последней точки отрезка xm = b. Наконец, решением системы алгебраических уравнений (9.9)
определяются значения искомых функций {u(b)}, которые можно рассматривать как начальные условия задачи (9.6), то есть фактически производится переход к задаче Коши.
9.3. Метод моментов
Для решения дифференциального уравнения второго порядка
|
|
|
′ |
′′ |
|
F(x, y(x), y (x), y (x)) = 0, x [a,b] |
|||||
с граничными условиями |
|
|
|
|
|
α0 y(a) + α1 y′x (a)= A, |
|||||
|
|
|
|
|
|
|
β |
|
y(b) + β |
y′ (b)= B. |
|
|
0 |
||||
|
|
|
1 |
x |
|
(9.12)
(9.13)
196

рассматриваются две специальные системы функций. Первая система функций {ψk }, k =1,2,…, называемых взвешивающими, удовлетворяет следующим
требованиям:
1) ψk C[a,b], k =1,2,…;
2) ψk , k =1,2,… образуют полную1 на [a, b] систему функции. Согласно [20] полными являются, например, системы функций:
– тригонометрических: 1, cos(nt), sin(nt), n = 1,2, … на отрезке [–π, π];
–полиномиальных: 1, t, t2 , … на любом произвольном отрезке [a, b];
–Эрмита2: Hk (t)e−t2 2 , k = 0, 1, 2, … на (–∞, ∞),
2 , k = 0, 1, 2, … на (–∞, ∞),
|
где H1 (t)= 2t , |
|
|
H2 (t) = 4t 2 − 2 , |
|
|
H3 (t)=8t3 −12t , |
|
– Лагерра3: Lk (t)e−t , |
H4 (t)=16t 4 − 48t 2 +12 , …; |
|
k = 0,1, 2, … на ( 0, ∞), |
||
|
где L1 (t) = −t +1, |
|
|
L (t)= t2 |
− 4t + 2 , |
|
2 |
|
|
L (t)= −t3 + 9t2 |
−18t + 6 , |
|
3 |
|
L (t) |
= t4 −16t3 + 72t 2 − 96t + 24 , … . |
|
4 |
|
|
1 Согласно [17] в гильбертовом пространстве L2 с нормой 
 x
x
 = (x, x)1
= (x, x)1 2 , порожденной
2 , порожденной
b
скалярным произведением (x, y) = ∫ x(t)y(t)dt , система элементов {ψk }, k =1,2,… является
a
полной, если не существует отличного от нуля элемента, ортогонального на [a, b] каждому
b
элементу ψk системы. Иначе, из условия ∫ y(t)ψk (t)dt = 0 следует, что y(t) = 0 t [a,b].
a
2Эрмит Шарль [24.12.1822 – 14.1.1901] – французский математик, был иностранным членом-корреспондентом и иностранным почетным членом Петербургской академии наук, членом Парижской академии наук и Лондонского королевского общества, профессором Парижского университета. Выполнил исследования в области классического анализа, алгебры, теории чисел, эллиптических функций, ортогональных многочленов.
3Лагерр Эдмон Никола [9.4.1834 – 13.8.1886] – французский математик, член Парижской академии наук. Основные труды выполнены в области геометрии, теории функций комплексного переменного, ортогональных многочленов.
197

Для второй системы пробных функций ϕk , k = 0,1,2,…, должны выполняться следующие условия:
1) ϕk C[2a,b], k = 0,1,2,…;
2)ϕk являются линейно независимыми на [a, b];
3)ϕ0 удовлетворяет граничным условиям (9.13),
α1ϕ0 (a)+ α2ϕ′0,x (a)= A, |
|||
|
|
||
|
|
||
β1ϕ0 (b)+ β2ϕ′0,x (b)= B; |
|||
|
|
||
остальные функции этой системы – однородным граничным условиям |
|||
α1ϕk (a)+ α |
2ϕ′k ,x (a)= 0, |
||
|
|
||
|
ϕ′k ,x (b)= 0, k =1, 2,…, |
||
β1ϕk (b)+ β2 |
|||
|
|
||
то есть |
|
||
k =1,2,... ϕk G ={v(x) C[2a,b] |
|
|
α1v(a) + α2v′x (a) = 0, β1v(b)+ β2v′x (b)= 0}. |
|
|||
4) ϕk , k = 0,1,2,…, образуют в G замкнутую1 систему функций. Для рассматриваемого случая это означает, что η G отыщется линейная комбинация функций ϕk , приближающая функцию η и ее производные сколь угодно
точно.
Решение задачи (9.12)–(9.13) разыскивается в виде разложения в ряд по пробным функциям ϕk , k = 0,1,2,…,
m |
|
ym (x) = ϕ0 (x) + ∑ak ϕk (x). |
(9.14) |
k=1 |
|
Нетрудно проверить, что функция ym (x) удовлетворяет граничным усло- |
|
виям (9.13) при любых значениях коэффициентов ak , k =1,m . В общем случае подстановка выражения (9.14) в уравнение (9.12) не обращает его в тождество:
F(x, ym , ym′ ,x , y′m′,xx )≠ 0
1 Согласно [14] замкнутой является такая система элементов {ϕk }, k = 0,1, 2,..., нор-
мированного пространства G, что любой элемент x G можно сколь угодно точно приблизить конечной линейной комбинацией элементов ϕk . Иными словами, ε > 0 найдутся та-
m
кие скаляры a1 ,a2 , …, an , что имеет место неравенство 
 x − ∑ak ϕk
x − ∑ak ϕk 
 < ε.
< ε.
k =1
198

в силу произвола в выборе коэффициентов ak , |
k = |
|
. Полученная невязка |
1,m |
|||
взвешивается в области [a, b] с помощью введенных функций ψ j , j =1,2,…, |
|||
b |
|
|
|
′ ′′ |
j =1, 2, … . |
||
μ j = ∫ F(x, ym , ym,x , ym,xx )ψ j dx, |
|||
a |
|
|
|
После интегрирования моменты μj являются функциями коэффициен- |
|||
тов ak , k =1,m , разложения (9.14) решения исходной задачи по пробным функциям. Полагая все μ j = 0 , получаемое выражение
b |
|
|
|
′ |
′′ |
… |
(9.15) |
∫ F(x, ym , ym,x , ym,xx )ψ j dx = 0, j =1, 2, |
|||
a
можно рассматривать как систему алгебраических уравнений, в общем случае нелинейных, относительно коэффициентов разложения решения дифференциальной задачи (9.12)–(9.13) в ряд (9.14) по замкнутой системе функций. Благодаря свойству полноты системы функций ψ j , j =1,2,…, условие (9.15) озна-
чает, что при m → ∞ невязка F (x, ym , y′m,x , y′m′,xx )= 0. Но это, в свою очередь,
приводит к тому, что ym → y, то есть разложение (9.14) сходится к реше-
m→∞
нию исходного дифференциального уравнения.
На практике ограничиваются решением конечной системы m алгебраических уравнений (9.15) c m неизвестными. Понятно, что повышение точности получаемого приближенного решения связано с повышением числа m слагаемых, удерживаемых в представлении (9.14).
Пример 9.2. Решить уравнение стационарной теплопроводности
(λθ′x (x))′x + J (x) = 0
для стержня единичной длины, теплоизолированного с боковой поверхности; полагается, что на левом и правом торцах поддерживается заданная температу-
ра θ(0) = θ0 , θ(1)= θ1 ; λ = const, J = const.
Система пробных функций строится на основе полиномов. В качестве «нулевой» выбирается линейная функция ϕ0 (x)= G + Hx. Коэффициенты G и H
подбираются |
из условия удовлетворения заданным граничным условиям |
||||
ϕ |
0 |
(0)= θ0 , ϕ |
(1)= θ1 |
, что позволяет определить G = θ0 |
и H = θ1 − θ0 . Таким об- |
|
1 |
|
|
||
разом, ϕ0 (x)= θ0 + (θ1 − θ0 )x.
199

Остальные пробные функции представляются в форме, удовлетворяющей однородным условиям задачи, например:
ϕ |
(x) = (x −1)x , ϕ |
2 |
(x)= (x −1)x2 , ϕ |
(x)= (x −1)x3 , …, |
ϕ |
k |
(x)= (x −1)xk. |
1 |
|
3 |
|
|
|
Понятно, что такое представление является неединственным. Для упрощения принято, что m = 3. Приближенное решение
y3 (x) = ϕ0 (x)+ a1ϕ1 (x)+ a2ϕ2 (x)+ a3ϕ3 (x)
подставляется в исходное дифференциальное уравнение:
F(x,y3 ,y3′,x ,y3′′,xx )= λ[2a1 + a2 (6x − 2) + a3 (12x2 − 6x)]+ J ≠ 0.
В качестве взвешивающих функций выбираются три первые элемента системы тригонометрических функций: 1, cos(t), sin(t).
Вычисляются значения моментов:
μ1 = ∫1 [2a1λ + a2λ(6x − 2)+ a3λ(12x2 − 6x)+ J ] 1dx = λ(2a1 + a2 + a3 )+ J ,
0
μ2 = ∫1 [2a1λ + a2λ(6x − 2)+ a3λ(12x2 − 6x)+ J ]cos(x)dx =
0
= 2a1λsin(1)+ a2λ[6cos(1)+ 4sin(1)− 6]+ a3λ[18cos(1) + 6sin(1) + 6]+ J sin(1),
μ3 = ∫1 [2a1λ+a2λ(6x −2)+a3λ(12x2 −6x)+ J]sin(x)dx =
0
= 2a1λ[1−cos(1)]+a2λ[6sin(1)−4cos(1)−2]+6a3λ[3sin(1)+3cos(1)−4]+ J[1−cos(1)].
Система линейных алгебраических уравнений (9.15) для рассматриваемой задачи принимает вид
2a1 + a2 + a3 = −J λ, |
|
|
|
|
|||||
|
|
|
[6cos(1) |
+ 4sin |
(1)− 6]+ a |
[18cos(1)+ 6sin(1)+ 6]= −J sin(1) λ, |
|||
2a sin(1)+ a |
2 |
||||||||
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
[6sin(1) − 4cos(1)− 2]+ 6a |
[3sin(1) + 3cos(1)− 4]= J[cos(1) −1] λ. |
|||
2a [1 − cos s(1)]+ a |
2 |
||||||||
|
1 |
|
|
|
|
|
3 |
|
|
Решением этой системы являются коэффициенты a1 = −J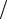 2λ, a2 = 0, a3 = 0 ,
2λ, a2 = 0, a3 = 0 ,
позволяющие представить решение в виде
y3 (x) = θ0 + (θ1 − θ0 )x − J (x −1)x 2λ = θ0 + (θ1 − θ0 + J 2λ)x − Jx2 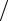 2λ.
2λ.
Полученное решение является точным для поставленной задачи.
200
