
mu_po_oformleniyu_mat_razdela_k_i_dp
.pdf
21
3. Введем рабочее множество P = {pi,jmin} объемов груза, поставляемого от поставщиков заказчикам при минимальной стоимости транспортировки. Множество (список) Р и есть начальный план перевозок, который в дальнейшем можно оптимизировать. Исходные значения перевозок: (i [1,m]) (j [1,n])
( pij = 0).
4. Вычислим суммарное количество запасов и заказов:
sa |
m tai ; sb |
n |
tbj . |
|
i 1 |
j |
1 |
5. Цикл пока (sa > 0) (sb > 0) не все запасы распределены и не все потребности удовлетворены:
5.1.Цикл i = 1..m по поставщикам:
5.1.1.Цикл пока tai > 0 – у i-того поставщика есть запас:
|
|
5.1.1.1. Зададим начальные значения: |
||
|
|
сmin = c11 – |
минимальная стоимость перевозок от |
|
|
|
i-того поставщика; |
||
|
|
jmin = 1 – координата cmin. |
||
|
|
5.1.1.2. Цикл j = 1..n поиска в i-той строке минималь- |
||
|
|
ной стоимости перевозки cmin и еѐ координаты jmin: |
||
|
|
если (tbj > 0) |
(cmin > ci,j), |
|
|
|
то cmin := сi,j, jmin:= j. |
||
|
|
5.1.1.3. Если tai |
tbjmin, |
|
|
|
то pi,jmin := tai, tbjmin := tbjmin – tai; tai := 0, |
||
|
|
иначе pi,jmin := tbjmin, tai := tai – tbjmin, tbjmin := 0. |
||
|
5.2. Вычислим остатки запасов и потребностей: |
|||
sa |
m tai ; sb |
n |
tbj . |
|
|
i 1 |
j |
1 |
|
Расчет потенциалов. В процессе решения после каждой итерации проверяется количество k загруженных клеток в таблице перевозок P:
k = 0; (i [1..m]) (j [1..n])(pi,j > 0) k := k + 1, т.е. для всех i от 1
до m и j от 1 до n, если pi,j > 0, то увеличить k на 1.
Если k m + n – 1, то план называется вырожденным и дальнейший расчет не возможен.
Потенциалы – это вспомогательные переменные, вводимые для проверки оптимальности плана.
Расчет потенциалов выполняют по загруженным клеткам, для которых должно выполняться следующее равенство:
i j cij ,
где i - потенциал i-того поставщика, j - потенциал j-того заказчика.
Алгоритм расчета потенциалов заключается в следующем:

|
|
|
|
22 |
|
|
1. |
Установим начальные значения потенциалов поставщиков: |
|||||
ALFA = { i}, i |
[1,m] такие, что |
( |
i |
ALFA) ( i = 0). |
||
2. |
Установим начальные значения потенциалов заказчиков: |
|||||
BETTA = { j}, j [1,n] такие, что |
( |
j |
BETTA) ( j = 0). |
|||
3. |
Установим начальные значения флажков, сигнализирующих о том, что |
|||||
потенциал поставщика уже рассчитан: |
|
|
|
|||
ZA = {zai}, i |
[1,m] такие, что |
(zai |
|
ZA) ( zai = 0). |
||
4. |
Установим начальные значения флажков, сигнализирующих о том, что |
|||||
потенциал заказчика уже рассчитан: |
|
|
|
|
||
ZB = {zbj}, j |
[1,n] такие, что |
(zbj |
|
ZB) ( zbj = 0). |
||
5. |
Установим начальные значения: |
|
|
|||
za1 = 1 – флажок потенциала первого поставщика;
k = 0 – количество загруженных клеток в плане перевозок.
6. Цикл пока k m + n.
6.1. Потенциал заказчика равняется стоимости первой перевозки к нему, уменьшенной на потенциал поставщика, если между ними есть перевозка и потенциал заказчика не вычислен и потенциал поставщика вы-
числен: |
|
|
|
|
|
|
|
|
|
(i |
[1,m]) |
(j |
[1,n]) (pij > 0) |
(zbj |
= 0) |
(zai |
= 1) |
||
( |
j = cij |
i) |
(zbj = 1) |
( k := k+1). |
|
|
|
||
6.2. Потенциал поставщика равняется стоимости первой перевозки |
|||||||||
от него, уменьшенной на потенциал заказчика, если между ними есть пе- |
|||||||||
ревозка и потенциал поставщика не вычислен, а потенциал заказчика вы- |
|||||||||
числен: |
|
|
|
|
|
|
|
|
|
(i |
[1,m]) |
(j |
[1,n]) (pij |
> 0) |
(zai = 0) |
(zbj |
= 1) |
||
( i = cij – j) ( zai = 1) ( k := k+1). |
|
|
|
||||||
Таким образом, если есть перевозка pij, то |
i = cij - |
j, |
j |
= cij - i , т.е. и то |
|||||
и другое равняется cij. |
|
|
|
|
|
|
|
|
|
Если нет ни одной перевозки от i-того поставщика, то |
|
i = 0, т.е. постав- |
|||||||
щик не загружен. |
|
|
|
|
|
|
|
|
|
Если нет ни одной перевозки от j-того поставщика, то |
|
j = 0, т.е. заказчик |
|||||||
не обслужен. |
|
|
|
|
|
|
|
|
|
Проверка плана на оптимальность. План считается оптимальным, если во всех его незагруженных клетках (в которых перевозки отсутствуют) выпол-
няется условие |
i + j |
cij, т.к. и поставщик и заказчик загружены: |
||
Flag=true; |
(i |
[1,m]) (j |
[1,n]) (pij = 0) |
( i + j > cij) |
(Flag=false). |
|
|
|
|
Если план не оптимален, то нужно продолжить вычисление. |
||||
Поиск звена максимальной неоптимальности. Звено максимальной не- |
||||
оптимальности находится как max( i + |
j - сi,j) среди незагруженных клеток. |
|||

23
Эту клетку необходимо загрузить за счет перераспределения ресурсов из других загруженных клеток. Клетку в таблице помечаем знаком "+", так как здесь в начальном плане находится вершина максимальной неоптимальности:
МЗН = c11; im = 1; jm = 1; |
|
||
(i [1,m]) |
(j |
[1,n]) ( i + j |
- cij > МЗН) |
(МЗН = |
i + |
j - cij) (im = i) |
(jm = j). |
Составление контура перераспределения ресурсов. Контур перерас-
пределения представляет собой многоугольник со сторонами, параллельными строкам и столбцам матрицы, и удовлетворяет следующим правилам:
1)все углы контура прямые;
2)в каждой вершине контура встречаются только два звена;
3)число вершин контура четное;
4)все вершины лежат на загруженных клетках, кроме клетки максимальной неоптимальности;
5)в каждой строке (столбце) матрицы имеются только две вершины: одна
-загружаемая, другая – разгружаемая.
Контур перераспределения ресурсов (КПР):
KR = {krk}, k [1,l], kr = <uik, ujk>,
где uik – i-координата k-той вершины контура; ujk – j-координата k-той вершины контура.
Введем функцию
true, если в i той строке и в j том столбце есть хотя бы ALL(i, j) одна загруженная клетка, кроме pij
false, иначе.
Алгоритм построения контура перераспределения ресурсов (КПР):
1. Введем рабочее множество TP = {tpij}, i [1,m], j [1,n], элементы которого в исходном состоянии совпадают с элементами множества P перевозок:
(i [1,m]) (j [1,n]) ( tpij = pij).
2.Установим Flag=false – флаг, сигнализирующий, что в таблице остались только вершины КПР.
3.Цикл пока Flag=false – для исключения перевозок, которые не могут быть перераспределены:
3.1.Переустановка Flag=true.
3.2.Обнуление перевозок, которые не могут быть перераспределены вдоль своей строки или столбца:
(i [1,m]) (j [1,n]) (tpij > 0) (ALL(i,j) = false) (tpij = 0)  (Flag=false).
(Flag=false).
4. Первая вершина КПР совпадает с элементом максимальной неопределенности
k = 1; ui1 = im; uj1 = jm.

|
24 |
5. Цикл пока (uik+1 |
im) (ujk+1 jm ) – пока не вернемся в точку нача- |
ла.
5.1.Увеличиваем индекс вершины КПР: k := k +1.
5.2.Если k – четное
то смещение вдоль строки i = uik-1, uik = i,
(j |
[1,n]) (tpij > 0) |
( ujk = j) – нашли перевозку, |
иначе смещение вдоль столбца: j= ujk-1, ujk = j, |
||
(i |
[1,m]) (tpij > 0) |
(uik = i) – нашли перевозку. |
6. Длина контура перераспределения l = k 1.
Поиск минимального элемента в контуре перераспределения. Пере-
распределение ресурсов по контуру осуществляется с целью получения оптимального плана. В процессе перераспределения ресурсов по контуру в соответствии с условием неотрицательности переменных х, ни одно из этих значений не должно превратиться в отрицательное число. Поэтому анализируют только разгружаемые клетки, из которых выбирают клетку с минимальным объемом перевозок (минимальный элемент в контуре):
MINEL = tpui1,uj1 ;
(k [2,l]) (MINEL > tpui |
,uj ) |
(MINEL = tpui |
,uj ). |
k |
k |
k |
k |
Перераспределение ресурсов по контуру производится очень просто:
при движении по столбцу от имеющихся компонентов плана надо отнимать минимальный элемент в контуре, а при движении по строке наоборот, прибавлять минимальный элемент в контуре:
(k [1,l]) ( pui |
,uj |
= pui |
,uj + MINEL Sign(k)), |
k |
k |
k |
k |
где функция Sign(k)
1, если k четное, 1, иначе.
5.3. Описание контрольного примера
Для описания контрольного примера возьмем процесс построения оптимального плана поставки продукции, выполняемый нашей программой и проведем его вручную.
Фирма имеет 3 склада на которых хранится картофель. С этой фирмой заключили договор на поставку картофеля 4 крупных магазина. Первому магазину необходимо 10 тонн картофеля, второму – 30, третьему – 70, четвертому – 30. На первом складе фирмы хранится 20 тонн картофеля, на втором – 40 тонн, на третьем 80 тонн. Необходимо получать оптимальный план поставки картофеля потребителям. Так же на основе статистических исследований известна стоимость доставки (в сот. руб.) из каждого склада в каждый магазин. Итак, мы имеем начальные данные, которые представлены в таблице 4.

25
|
|
|
|
|
Таблица 4 |
|
|
Исходные данные |
|
|
|
|
|
|
|
|
|
ПН |
|
|
|
|
Запасы |
ПО |
В1 |
В2 |
В3 |
В4 |
аi |
А1 |
4 |
2 |
4 |
3 |
|
|
|
|
|
|
20 |
А2 |
2 |
3 |
1 |
6 |
|
|
|
|
|
|
40 |
А3 |
3 |
4 |
5 |
2 |
|
|
|
|
|
|
80 |
Заявки |
|
|
|
|
|
bj |
10 |
30 |
70 |
30 |
140 |
Методом минимальной стоимости по строке определяем начальный план: Таблица 5
Начальный план
ПН |
|
|
|
|
Запасы |
ПО |
В1 |
В2 |
В3 |
В4 |
аi |
А1 |
4 |
2 |
4 |
3 |
|
|
|
20 |
|
|
20 |
А2 |
2 |
3 |
1 |
6 |
|
|
|
|
40 |
|
40 |
А3 |
3 |
4 |
5 |
2 |
|
|
10 |
10 |
30 |
30 |
80 |
Заявки |
|
|
|
|
|
bj |
10 |
30 |
70 |
30 |
140 |
Расчет потенциалов загруженных и незагруженных клеток: Таблица 6
Расчет потенциалов
ПН |
|
|
|
|
|
|
ПО |
В1 |
В2 |
В3 |
В4 |
|
i |
А1 |
4 |
2 |
4 |
3 |
|
0 |
|
с = 1 |
20 |
с =3 |
с =0 |
|
|
А2 |
2 |
3 |
1 |
6 |
|
-2 |
|
с = 1 |
с = 0 |
40 |
с = |
2 |
|
А3 |
3 |
4 |
5 |
2 |
|
2 |
|
10 |
10 |
30 |
30 |
|
|
j |
|
|
|
|
|
|
|
1 |
2 |
3 |
0 |
|
|
|
|
|
|
|
|
|
Проверка плана на оптимальность по незагруженным клеткам:
26
|
План оптимальный, т.к для всех незагруженных клеток выполняется |
i |
j cij . |
Общие транспортные издержки:
Z = 360 сот. руб.
Итак, в результате построения плана поставки мы выяснили что мы достигнем минимальных транспортных издержек в том случае если:
Из 1-го склада доставим во 2-й магазин 20 тонн картофеля. Из 2-го склада доставим 40 тонн в 3-й магазин.
Из 3-го склада доставим в 1-й магазин 10 тонн, во 2-й магазин 10 тонн, в 3-й магазин 30 тонн, в 4-й магазин 30 тонн. При этом общие транспортные издержки составят 360 сот. руб.
6. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ НАХОЖДЕНИЯ МАКСИМАЛЬНОЙ ПЛОЩАДИ ОКРУЖНОСТИ ВНУТРИ ЧЕТЫРЕХУГОЛЬНИКА
Найти площадь максимальной окружности, которую можно нарисовать внутри произвольного четырехугольника.
Дано:
A, B, C, D T,
где T = {(x, y) | x, y 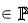 } – множество точек евклидовой плоскости, на которой задана декартова прямоугольная система координат xOy.
} – множество точек евклидовой плоскости, на которой задана декартова прямоугольная система координат xOy.
Q = (A, B, C, D) – четырехугольник ABCD, где A, B, C, D T (рис. 6.1).
Рис. 6.1
Найти:
S – максимальная площадь окружности, которую можно нарисовать внутри четырехугольника ABCD, S 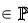 .
.

27
Далее приведен метод решения задачи в аналитической форме и в алгоритмической.
6.1. Аналитическая форма представления метода
Искомое значение максимальной площади S окружности, которая лежит внутри четырехугольника ABCD, можно получить в результате ряда экспериментов:
|
|
|
S = max Square(Oi), |
|
|
|||
|
|
|
|
|
i |
|
|
|
где |
Oi = ( i, |
i) – окружность, i = 0, ... n, n – количество произведенных экспе- |
||||||
риментов, n |
; |
|
|
|
|
|
|
|
|
i – центр окружности Oi, |
i |
|
T, Inside( i, Q) = 1; |
|
|||
|
|
1, если t расположена внутри геометрической фигуры F; |
||||||
|
Inside (t, F)= 0, если t расположена вне геометрической фигуры F. |
|||||||
|
t T, F = (pt1, pt2, …, ptm) – геометрическая фигура, вершинами которой |
|||||||
являются точки pt1, pt2, …, ptm |
T, m |
; |
|
|
|
|||
|
i – радиус окружности, |
i |
. |
|
|
|
||
|
Окружности Oi находятся внутри четырехугольника Q: |
|||||||
|
|
( s T)(Inside(s,Oi)=1) |
(Inside(s,Q)=1). |
|||||
|
Функция, возвращающая площадь окружности Oi = ( |
i, i): |
||||||
|
|
Square (Oi) = |
i2, i = 0, ... n. |
(6.1) |
||||
|
Определим функцию Inside(t, Q), характеризующую положение точки t |
|||||||
T по отношению к четырехугольнику Q: |
|
|
|
|||||
Inside(t, Q) = Inside(t, QT1) Inside(t, QT2), где QT1 |
и QT2– треугольники такие, |
|||||||
что QT1 = (q , q mod 4 + 1, q( +1) mod 4 + 1), QT2 = (q , q( +1) mod 4 +1, q( +2) mod 4 + 1), |
||||||||
где |
– такое натуральное число от 1 до 4, что u > 180 , если Q – невыпуклый |
|||||||
четырехугольник, или произвольное натуральное число от 1 до 4, если Q – вы- |
||||||||
пуклый четырехугольник (рис. 6.2). |
|
|
|
|
|
|||
|
Углы четырехугольника: U=( |
|
DAB, |
ABC, |
BCD, |
CDA). |
||
|
Вершины четырехугольника qj |
Q = (A, B, C, D), j = 1, …, 4. |
||||||
Пусть вершины треугольника Tr имеют координаты (x1,y1), (x2,y2), (x3,y3). Значение функции Inside (t, Tr), характеризующее принадлежность точки t треугольнику Tr, определяется как истинность равенства площади Tr сумме площадей трех треугольников, образованных точкой t и каждой из трех сторон Tr
(рис. 6.3):
1, если Square (Tr) = Square (t, (x1, y1), (x2, y2)) +
Inside(t, Tr) = |
+ Square (t, (x2, y2), (x3, y3)) + Square (t, (x3, y3), (x1, y1)); |
|
0, иначе, |
где Square (Tri) – функция, возвращающая площадь треугольника Tri = (pt1, pt2, pt3), pt1, pt2, pt3 T:
Square (Tri) = 
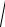 p p a p b p c .
p p a p b p c .
28
Длины сторон треугольника: a = length(pt1, pt2), b = length(pt2, pt3), c = length(pt3, pt1),
где length(l) – функция, возвращающая длину отрезка l = (pt1, pt2), pt1, pt2
T. Вершины треугольника – точки pt1 |
и pt2 имеют координаты (x1, y1) и (x2, |
|||
|
|
|
|
|
y2) соответственно. Тогда length(l) = (x2 |
x1)2 |
(y2 y1)2 . |
||
Полупериметр треугольника Tri: p |
a b |
c . |
||
|
|
2 |
|
|
Рис. 6.2
Рис. 6.3
Определим значение функции Inside (t, Oi), характеризующей положение точки t T по отношению к окружности Oi = ( i, i), i = 0, … n:
1,
Inside (t, Oi)= 0,
если length( i, t) ≤ i;
иначе.
Пусть окружность максимального радиуса была получена в результате n- го эксперимента: S = Square (On). Square(On) = 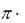 n2, из чего следует, что внутреннюю для четырехугольника окружность максимальной площади можно искать как внутреннюю окружность максимального радиуса. Рассмотрим порядок непосредственного нахождения значения максимального радиуса n внутренней окружности для четырехугольника Q.
n2, из чего следует, что внутреннюю для четырехугольника окружность максимальной площади можно искать как внутреннюю окружность максимального радиуса. Рассмотрим порядок непосредственного нахождения значения максимального радиуса n внутренней окружности для четырехугольника Q.

29
Проверим выпуклость четырехугольника Q. Один из критериев выпуклости многоугольника – одинаковый знак определителей всех пар его смежных сторон. Основываясь на этом свойстве, рассмотрим возможные значения суммы этих определителей
sign |
|
|
xA |
xD |
yA |
yD |
|
sign |
|
|
xB |
xA |
yB |
yA |
|
|
|||
|
|
|
|
|
|
|
|||||||||||||
|
|
xB |
xA |
yB |
yA |
|
|
|
xC |
xB |
yC |
yB |
|
(6.2) |
|||||
sign |
|
xC |
xB |
yC |
yB |
|
|
sign |
|
xD |
xC |
yD |
yC |
|
, |
||||
|
|
|
|
|
|
||||||||||||||
|
|
xD |
xC |
yD |
yC |
|
|
|
|
xA |
xD |
yA |
yD |
|
|
|
|||
где (xA, yA), (xB, yB), (xC, yC), (xD, yD) – координаты точек A, B, C и D соответственно.
Выпуклый четырехугольник (| | = 4). Случаю выпуклости четырех-
угольника Q соответствует значение | | = 4 (все определители (6.2) имеют одинаковый знак).
Для выпуклого четырехугольника внутренняя окружность максимального радиуса касается минимум трех его сторон (рис. 6.4). Следовательно, центр такой окружности лежит на пересечении биссектрис двух углов, имеющих общую сторону. Радиус окружности с центром в этой точке определяется как минимальное из расстояний от этой точки до каждой из сторон.
|
|
|
|
yq |
yq |
xM |
xq |
xq |
yM |
xq |
yq |
xq |
yq |
|
||
|
|
max |
min |
k |
k mod 4 1 |
|
ij |
k mod 4 1 |
k |
ij |
k |
k mod 4 1 |
k mod 4 1 |
k |
, (6.3) |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
i, j |
1...4 ; |
k 1 4 ; |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
j |
i |
1, 1 i 3; |
Inside(Mij ,Q) 1 |
|
|
|
xqk mod 4 1 xqk |
|
yqk mod 4 1 |
yqk |
|
|
|
|||
1, i 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где Mij – точка пересечения биссектрис углов ui и uj четырехугольника Q, та-
кая, что Inside(Mij, Q) = 1;
qp – вершины четырехугольника Q = (A, B, C, D), p = 1, …, 4;
xpt, ypt – координаты точки pt T, xpt, ypt 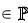 .
.
Уравнение биссектрисы угла, образованного поворотом прямой, заданной нор-
мированным уравнением xcos |
1 + ysin |
1 – |
1 = 0;, против часовой стрелки до |
||
положения xcos 2 + ysin 2 – 2 = 0, где |
, |
, |
{1, 2}, определяется как |
||
(xcos 1 + ysin |
1 – 1) + (xcos |
2 + ysin 2 – 2) = 0. |
(6.4) |
||
На рис. 6.4 представлен пример построения внутренней окружности максимального радиуса при i = 1, j = 2.

30
Рис. 6.4
Четырехугольник с самопересечением (| | = 0). Случаю четырехуголь-
ника с самопересечением (рис. 6.5) соответствует значение | | = 0 (два определителя (6.2) положительны, два – отрицательны).
Рис. 6.5
Назовем такое натуральное число из множества {1, 2}, что
( L T) L = CrossingPoint ((q , q |
mod 4 + 1), (q( |
+ 1) mod 4 + 1, q( |
+ 2) mod 4 + 1)), (6.5) |
|||||||
где qj – вершины четырехугольника Q = (A, B, C, D), j = 1, …, 4, |
|
|||||||||
CrossingPoint((eн1, eк1), (eн2, eк2)) – функция, возвращающая точку пересе- |
||||||||||
чения отрезков (eн1, eк1) и (eн2, eк2); eн1, eк1, eн2, eк2 |
T. |
|
|
|
|
|
|
|||
Определим порядок нахождения точки пересечения: |
|
|
|
|
|
|||||
(–1, –1) (отрезки не пересекаются), |
|
|||||||||
если |
|
xeн2 |
xeк2 |
yeн2 |
yeк2 |
|
=0 |
( |
1 [0; 1]) |
|
Det |
|
|||||||||
|
|
xe1к |
xe1н |
ye1к |
ye1н |
|
|
|
|
|
CrossingPoint((eн1,eк1),(eн2,eк2))= |
( |
2 |
[0; 1]) = 0; |
|
|
|
|
|
||
x 1 |
1 x 1 |
|
x 1 |
, y 1 |
1 |
y 1 |
y 1 |
, |
||
eн |
eк |
|
eн |
eн |
|
eк |
|
eн |
|
|
если (Det |
0) |
( |
1 [0; 1]) |
( |
|
2 |
[0; 1]) = 1, |
|||
