2.7.Зависимость теплоёмкости от температуры. Истинная и средняя теплоёмкости.

Опытные значения теплоёмкостей при различных температурах представляются в виде таблиц, графиков и эмпирических функций.

Различают истинную и среднюю теплоемкости.

Истинная теплоемкость C-это теплоемкость для заданной температуры.

В инженерных расчетах часто используется среднее значение теплоемкости в заданном интервале температур (t1;t2).

Средняя теплоемкость обозначается двояко: ,.

Недостаток последнего обозначения является незаданность диапазона температур.

Истинная и средняя теплоемкости связаны соотношением:

(81)

Истинная теплоемкость-это предел, к которому стремится средняя теплоемкость, в заданном диапазоне температур t1…t2, при ∆t=t2-t1

Как показывает опыт, у большинства газов истинные теплоемкости возрастают с ростом температуры. Физическое объяснение этого возрастания заключается в следующем:

Известно, что температура газа не связана колебательным движением атомов и молекул, а зависит от кинетической энергии E_k поступательного движения частиц. Но по мере роста температуры подводимая к газу теплота всё более и более перераспределяется в пользу колебательного движения, т.е. рост температуры при одинаковом подводе теплоты по мере роста температуры замедляется.

Типичная зависимость теплоемкости от температуры:

c=c₀ + at + bt² + dt³ + … (82)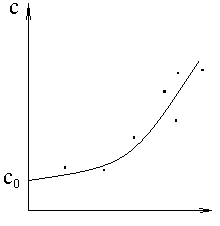

где c₀, a, b, d – эмпирические коэффициенты.

c – Истинная теплоёмкость, т.е. значение теплоёмкости для заданной температуры T.

Для теплоемкости битоппроксимирующей кривой- это полином в виде ряда по степеням t.

Аппроксимирующая кривая проводится с использованием специальных методов, например, методом наименьших квадратов. Суть этого метода в том, что при его использовании все точки примерно равноудалены от аппроксимирующей кривой.

Для инженерных расчётов, как правило, ограничиваются двумя первыми слагаемыми в правой части, т.е. полагают зависимость теплоёмкости от температуры линейной c=c₀ + at (83)

_{Средняя теплоемкость графически определяется как средняя линия заштрихованной трапеции, как известно средняя линия трапеции определяется как полусумма оснований.}

Формулы применяются, если известна эмпирическая зависимость.

В тех случаях, когда зависимость теплоёмкости от температуры не удаётся удовлетворительно аппроксимировать к зависимости c=c₀+at, можно воспользоваться следующей формулой:

(85)

Эта формула применяется в тех случаях, когда зависимость c от t существенно нелинейна.

Из молекулярно-кинетической теории газов известно

U_ = 12,56T ,U_ - внутренняя энергия одного киломоля идеального газа.

Ранее было получено для идеального газа:

, ,

_{Из полученного результата следует, что теплоемкость, полученная с использованием МКТ, от температуры не зависит.}

Уравнение Майера: c_p-c_v=R_,

c_p=c_v+R_=12,56+8,31420,93.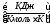

Как и предыдущем случае по МКТ газов молекулярная изобарная теплоемкость от температуры не зависит.

Понятию идеального газа в наибольшей степени соответствуют одноатомные газы при малых давлениях, на практике приходится иметь дело с 2-х, 3-х … атомными газами. Например, воздух, который по объёму состоит из 79% азота (N₂), 21% кислорода (O₂) (в инженерных расчетах инертные газы не учитываются в силу малости их содержания) .

Можно для оценочных расчётов пользоваться следующей таблицей:

Газ	cv	cp,
одноатомный	12,56	20,93
двухатомный	20,93	29,31
трехатомный	29,31	37,68

У реальных газов, в отличие от идеального, теплоёмкости могут зависеть не только от температуры, но и от объёма и давления системы.