17. Системы лду с постянными коофицентами.

18. Лоду н-го порядка с постоянными коофицентами. Уравнения Эйлера.

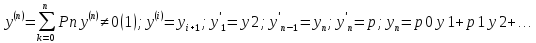
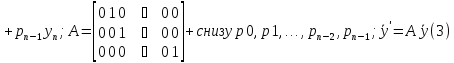
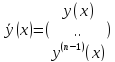(2) (5) – ФСР сист 2 и 3

=

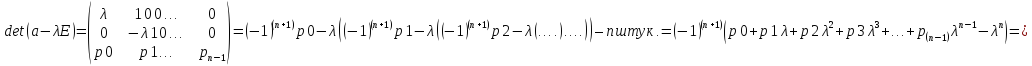
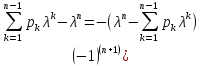
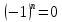
(𝜆)=0 (6); (𝜆)=𝜆^n-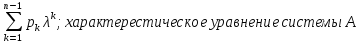

Ly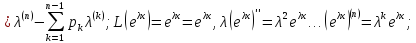

=

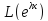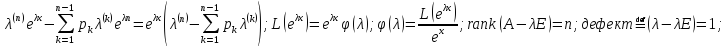
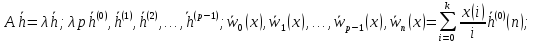
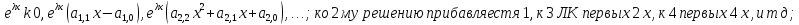
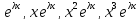
1 вывод

Если -корень характерестического уравнения ЛОДУ с постоянными коофицентами, кратности р, то ФСР ЛОДУ ему соответствует функция 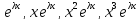, если𝜆-действительн переменнаяБ то все ОК

Если комплексная, то комплексному корню сооответсвует сопряженный корень.

Полученны пары комплексно-сопряженных решений.

Переход от Комплексного к действительному решению.

Пусть u(x)+v(x)i

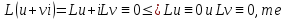
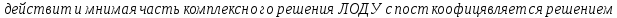
Вывод.

В паре комплексно-сопряженных корней

; кратность р ФСР ЛОДУ ур (1) соответсвует функции

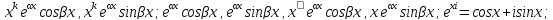
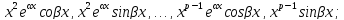
Уравнение Эйлера

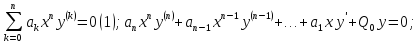
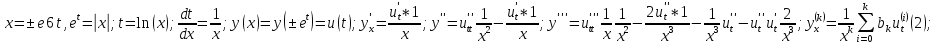
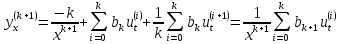
(2) оправдано при k=0 1, 2 ,3. При к произвольном следует его справедливость для k+1=>2 верно для любого

()

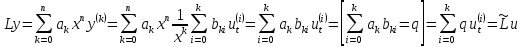
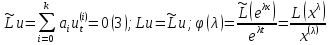
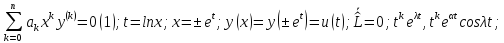
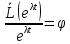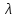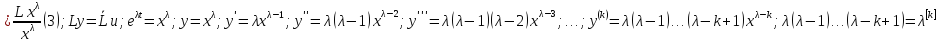
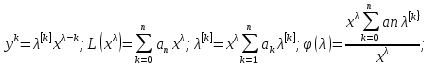
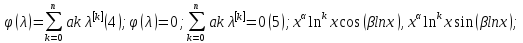
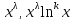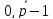Если 𝜆 –действительный корень характерестического уравнения (5)б уравнениеЭйлера (1), кратности р, то ему соответсвует ФСР ур (1), соответсвует функцииk=; 𝜆=

Характерестическое уравнение (5) в ФСР ур (1) соответсвует функц

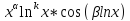
; k=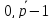

19.Вроонскиан, теоремы о вронскианал. Построение лоду по фср

20.Формулировки Лиувилля и Остроградского Лиувилля.

21. Решение системы неоднородных ЛНДУ методом Лагранжа, формула Коши, матрица коши.

22.Решение ЛНДУ н-го порядка методом Лагранжа, функция Коши, формула Коши.

Опред.Функция Коши ЛОДУ (10) называется функцией K(x,s) в кот при каждом фиксированном s, каждая ф-ция является решением однородного ЛОДУ (10) удволетворяющего условиям.

23. Функция Коши. Ее построение по ФСР.

Функция Коши ;См билет выше;

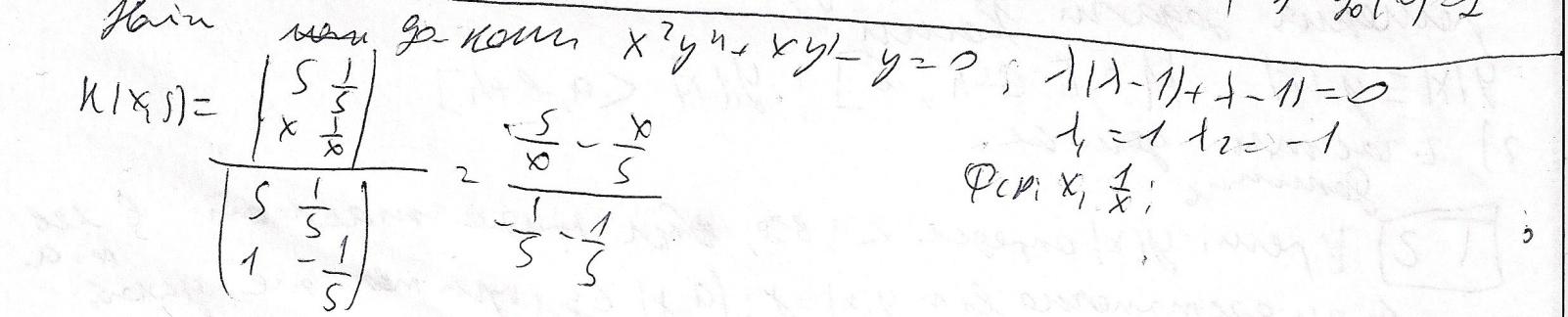
24. Метод неопрделенных коофицентов при в=0, они вместе там искать надо,

25 Метод неопрделенных коофицентов при в≠0

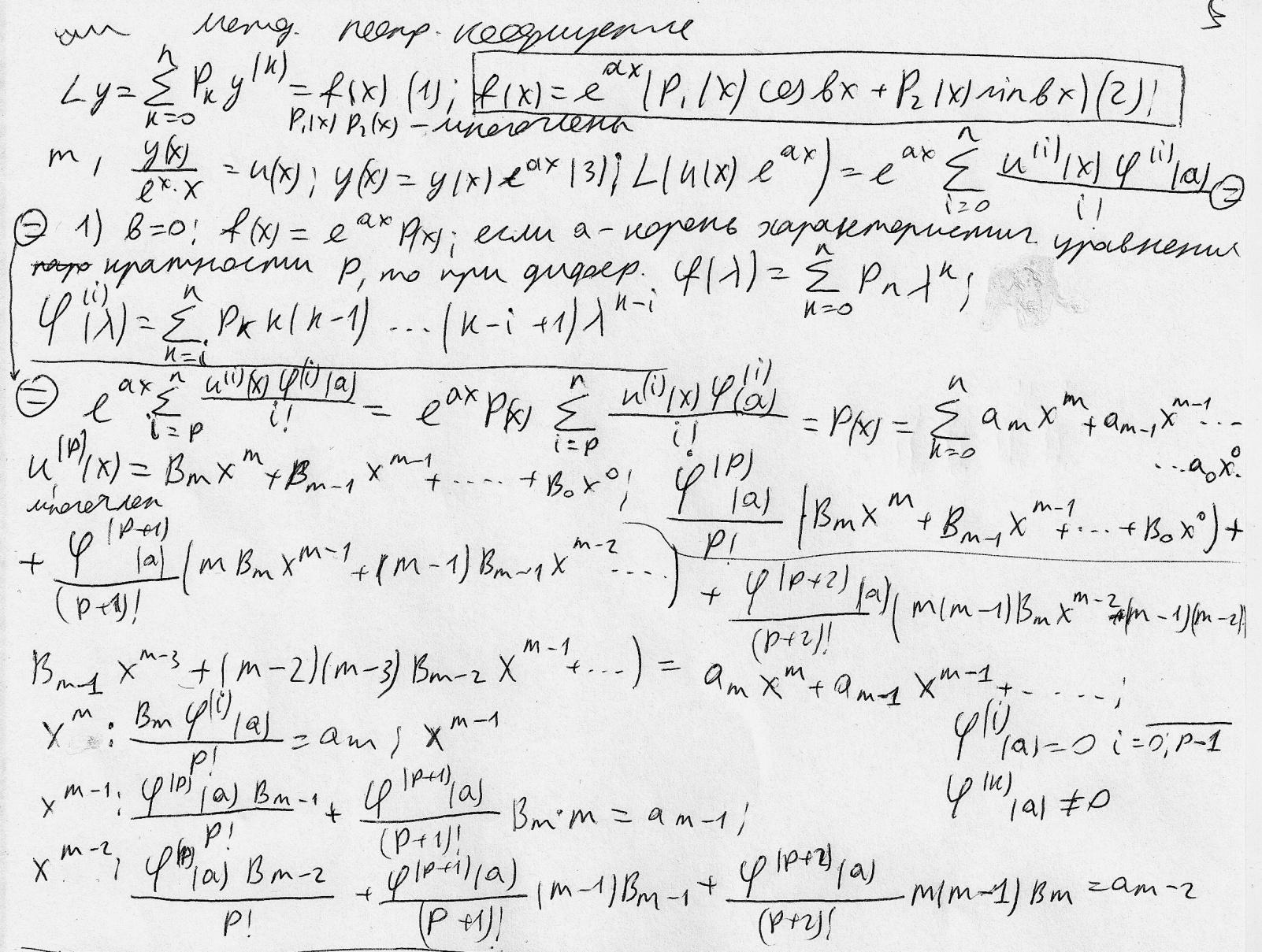
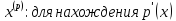­.придется интегрировать р-раз,пологая,при каждом интегрировании пр-я=0;молучим многочлен с младшим членом 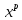,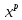можно вынести.

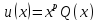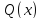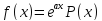;- многочлен степениn; ур 1 с прав частью ;многочлен степениm; имеет частное решение вида-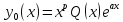

p –кратность а; как корня характерестического уравнения.

Всё это пригодно и для комплексных чисел.

ЛНДУ со свобод. Вида 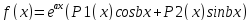имеет частное решение

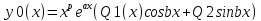p –кратность s=a+bi; как корня характерестического уравнения.

26. Продолжение решений ду, условие продолжимотти., непродолжаемые решения.

Опред: Решение y(x) ур(1) опр на <а, b >, называется непродолжающимся если не существует его продолжения y1(x) на <a,b>

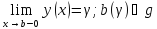
2 Часть доказательства.

Пусть решение

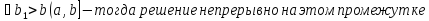
Значит 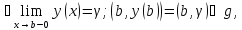иначе y(x) не может удволетворять уравнению в т b. Теорема доказана.

Т2. Для всех y(x) опред на <a,b>, былпрололжаем в лев. т. А, необходимо и достаточно, чтобы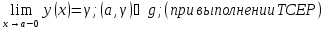

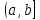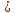Док-во. По Т1 получим, что если решение определено на , то решение продолжается вправо, а еслито решение продолжается влево (к точке а)

Следствие

Если условие ТСЕР выполняется в открытой области,то макс. Промежутком непродолжит. решения может быть только интервал.

27. Теорема о существовании непродолжаемого решения задачи Коши.

Что [x-h,x+h] ур (1) имеет единственоое решение удволетворябщее условию y(x)=y1

. Т к y(x) непродолж решение, то ;

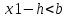
конец.

29.Собственные значения и собственные функции краевых задач.