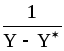2) Для определения числа единиц переноса методом графического интегрирования по данным табл. 1.4 и рис. 1.6 составляем табл. 1.5.

По данным последней таблицы строим график 1/(Y-Y)=f(Y) -рис. 1.7. Подсчитываем на этом графике отмеченную штриховкой площадь (например методом трапеций)

Т а б л и ц а 1.5

X	Y	Y	Y-Y
0	0,003	0	0,003	333
0,005	0,0097	0,0045	0,0052	193
0,010	0,0165	0,0102	0,0063	159
0,0125	0,0200	0,0138	0,0062	161
0,015	0,0234	0,0183	0,0051	196
0,020	0,0300	0,0273	0,0027	371

Величина этой площади (5,83) дает значение интеграла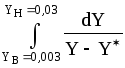, т. е. число единиц переноса n_0у.

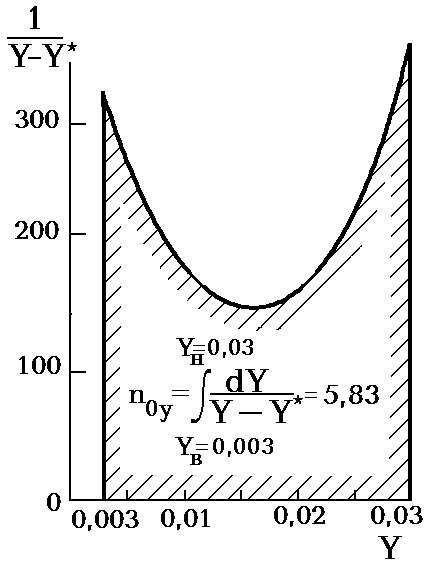
Рис 1.7 Определение числа единиц переноса методом графического интегрирования (к примеру 1.10).

Пример 1.11. Определить теоретически минимальный расход жидкого поглотителя с мольной массой 224 кг/кмоль, необходимый для полного извлечения пропана и бутана из 1000 м³/ч (считая при нормальных условиях) газовой смеси. Содержание пропана в газе 15% (об.), бутана 10% (об.). Температура в абсорбере 30С, абсолютное давление 3 кгс/см² (294 кПа). Растворимости бутана и пропана в поглотителе характеризуются законом Рауля.

Р е ш е н и е . Максимальная концентрация (мольная доля) пропана в поглотителе, вытекающем из скруббера (равновесная с входящим газом), определяется по уравнению (1.8):

,

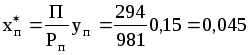где Р_п=981 кПа (10 кгс/см²)-давление насыщенного пара пропана при 30С.

Количество содержащегося в газовой смеси пропана, которое требуется поглощать:

G_п=Vy_п/22,4=10000,15/22,4=6,7 кмоль/ч.

Минимальный расход поглотителя для поглощения пропана определяется из уравнения:

,

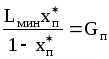откуда

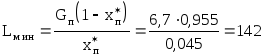кмоль/ч,

или 142224=31 800 кг/ч.

Наибольшая возможная концентрация бутана в поглотителе, вытекающем внизу из скруббера:

,

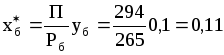где Р_б=265 кПа (2,7 кгс/см²)- давление насыщенного пара бутана при 30С.

Количество поглощаемого бутана:

G_б=Vy_б/22,4=10000,1/22,4=4,47 кмоль/ч.

Минимальный расход поглотителя для поглощения бутана:

L_мин=G_б(1-х_б)/х_б=4,470,89/0,11=36,1 кмоль/ч.

Минимальный расход поглотителя для полного поглощения бутана значительно меньше, чем для поглощения пропана, следовательно, найденным выше количеством поглотителя (142 кмоль/ч) бутан будет полностью уловлен.

Пример 1.12. Определить коэффициент массоотдачи для газовой фазы в насадочном абсорбере, в котором производится поглощение диоксида серы из инертного газа (азота) под атмосферным давлением. Температура в абсорбере 20С, он работает в пленочном режиме. Скорость газа в абсорбере (фиктивная) 0,35 м/с. Абсорбер заполнен кусками кокса (=42 м²/м³, V_св=0,58 м³/м³).

Р е ш е н и е . По уравнению (1.45):

,

где

;

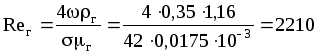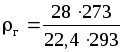=1,16 кг/м³; _г=0,17510^-3 Пас (рис. VI).

Коэффициент диффузии D_г принимаем такой же, как в воздухе.

Имеем:

D_г=10,310^-6(293/273)^1,5=11,4510^-6 м²/с (табл. XLII);

.

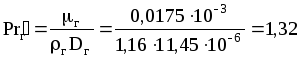Диффузионный критерий Нуссельта:

Nu_г=_гd_э/D_г=0,4072210^0,6551,32^0,33=69.

Эквивалентный диаметр:

d_э=4V_св/=40,58/42=0,055 м.

Коэффициент массоотдачи:

_г= Nu_гD_г/d_э =6911,4510^-6/0,055=14410^-4 м/с.

Пример 1.13. Из критериального уравнения (1.45) вывести расчетную формулу для определения высоты единицы переноса по газовой фазе.

Р е ш е н и е . Из уравнения (1.12)

,

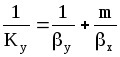В котором К_у, _у и _х выражены в кмоль/(м²с), получаем

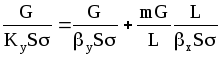
или в соответствии с уравнением (1.43) при =1

.

Здесь G и L -мольные расходы газа и жидкости, кмоль/с; S-поперечное сечение абсорбера, м²; -удельная поверхность насадки, м²/м³; h_y=G/(_yS)-высота единицы переноса для газовой фазы, м; h_x= L/(_xS)-то же для жидкой фазы, м.

В критериальном уравнении (1.45)

Nu_г=0,407Re_г^0,65(Pr_г)^0,33,

где 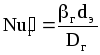, коэффициент массоотдачи _г выражен в 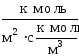=м/с.

Соотношение между _у и _г находим из уравнения:

_уу=_гС_у,

откуда

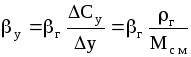(см табл. 1.2.)

Тогда

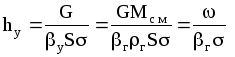и ,

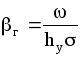где 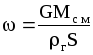- фиктивная скорость, м/с.

Подставляя найденное значение _г в выражение для диффузионного критерия Нуссельта, получаем:

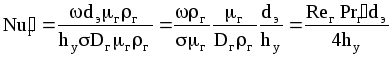
и из уравнения (1.45):

h_y=0,615d_эRe_г^0,345(Pr_г)^0,67.

Пример 1.14. В скруббере с насадкой из керамических колец 50  50  5 мм (навалом) производится поглощение диоксида углерода водой из газа под давлением р_абс=16 кгс/см² (1,57 Мпа) при температуре 22С. средняя мольная масса 20,3 кг/моль, динамический коэффициент вязкости газа при рабочих условиях 1,3110^-5 Пас, коэффициент диффузии СО₂ в инертной части газа 1,710^-6 м²/с. Средняя фиктивная скорость газа в скруббере 0,041 м/с, плотность орошения (фиктивная скорость жидкости) 0,064 м³/(м²с). Определить общую высоту единицы переноса h_0у, принимая коэффициент смоченности насадки  равным единице.

Р е ш е н и е . Общая высота единицы переноса (см. предыдущий пример):

.

Находим h_y-высоту единицы переноса для газовой фазы:

h_y=0,615d_эRe_г^0,345(Pr_г)^0,67.

Характеристики насадки V_св=0,785 м³/м³ и =87,5 м²/м³ берем из табл. XVII. Таким образо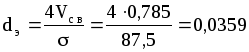м,

м;

.

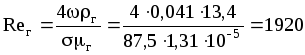Здесь

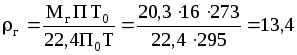кг/м³;

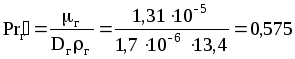
Высота единицы переноса для газовой фазы:

h_y=0,6150,03591920^0,3450,575^0,67=0,205 м.

Находим h_x -высоту единицы переноса для жидкой фазы по формуле

h_х=119_прRe_ж^0,25(Pr_ж)^0,5,

полученной из уравнения (1.46) так же, как в предыдущем примере из уравнений (1.45) получено выражение для h_y.

Значения физико-химических свойств для воды при 22С: _ж=1000 кг/м³; _ж=0,95810^-3 Пас (пз табл. VI); D_ж=1,8710^-9 м²/с (табл. XLIII).

Приведенная толщина жидкой пленки:

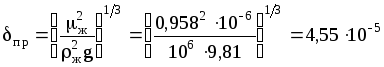м.

По условию плотность орошения:

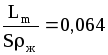м³/(м²с),

где L_m-массовый расход жидкости, кг/с.

Массовая плотность орошения:

L_m/S=0,064_ж=64 кг/(м²с).

По уравнению (1.50):

.

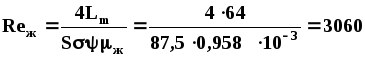
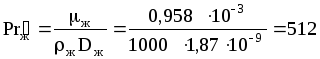Высота единицы переноса для жидкой фазы:

h_x=1194,5510^-53060^0,25512^0,5=0,91 м.

Находим отношение мольных расходов газа и жидкости G/L. Из уравнения расхода для газа =GM_г/(_гS) получаем:

G/S=_г/M_г=0,04113,4/20,3=0,0271 кмоль/(м²с).

Для жидкости:

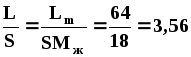кмоль/(м²с).

Отсюда

G/L=0,0271/3,56=0,00761.

Коэффициент распределения m в уравнении (1.12):

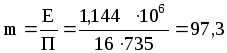-см. уравнение (1.3),

где коэффициент Генри Е=1,14410⁶мм рт. ст. (при 22С) получен интерполяцией данных табл. XLI.

Общая высота единицы переноса:

h_0y=h_y+ h_x⁼0,205+97,30,007610,91=0,205+0,675=0,88 м.

Пример 1.15. По данным примера 1.8 определить число единиц переноса в абсорбере с учетом обратного (продольного) перемешивания.

Р е ш е н и е. Число единиц переноса для условий идеального вытеснения, т. е. без учета обратного перемешивания, составляет:

n_0y=(Y_н-Y_в)/Y_ср=(0,0639-0,00128)/0,0079=7,93.

Искомое число единиц переноса с учетом обратного перемешивания n_0y находим из уравнения

,

в котором поправка на обратное перемешивание n_обр равняется:

.

где А= ; Ф=1-.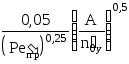

Значение критерия Pe_пр вычисляют по уравнению:

.

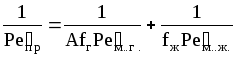Здесь 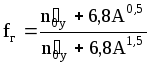; ; 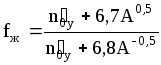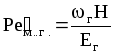, Pe_м.ж=_жН/Е_ж - модифицированные критерии Пекле для газа и жидкости; _г, _ж - скорости потоков газа и жидкости, м/с; Е_г ,Е_ж - соответствующие коэффициенты обратного перемешивания, м²/с; Н - рабочая длина аппарата, высота слоя насадки, м.

По данным примера 1.8 находим:

,

;

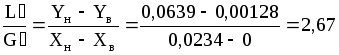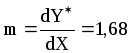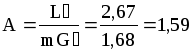
Примем предварительно n_0y=9. Тогда

; .

Для определения скоростей газа и жидкости (_г и _ж) необходимо найти доли поперечного сечения абсорбера, занимаемые каждым потоком в отдельности. Долю объема насадки , занятую жидкостью, рассчитаем по уравнению:

=4,8310^-4Г^0,435/d_э^0,24,

в котором

Г= кг/(см)

d_э=4V_св/=40,74/204=0,0145 м.

Подставляя эти значения, находим:

=4,8310^-42040,0114^0,435/0,0145^0,.24=0,039.

Скорость течения жидкости в слое насадки:

м/с

Скорость газа:

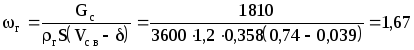
м/с.

Величины коэффициентов обратного перемешивания Е_ж и Е_г находят опытным путем. для ориентировочного их определения в насадочном абсорбере воспользуемся критерильными уравнениями.

Для жидкой фазы:

_жd_н/Е_ж=7,5810^-3Re_ж^0,703.

Для газовой фазы:

_гd_н/Е_г=2, 4.

В этих уравнениях:

; ,

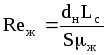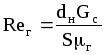где d_н - номинальный размер элементов насадки, м.

В нашем случае:

;

.

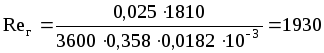Для жидкой фазы:

_жd_н/Е_ж=7,5810^-3 58^0,703=13010^-3.

Коэффициент обратного перемешивания в жидкой фазе:

Е_ж=_жd_н/0,13=0,060,025/0,13=0,0116 м²/с;

Pe_{м. ж.}=_жН/Е_ж=0,0616,8/0,0116=87.

Для газовой фазы:

.

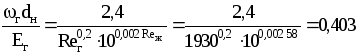Коэффициент обратного перемешивания в газовой фазе:

Е_г=_гd_н/0,403=1,670,025/0,403=0,104 м²/с;

Pe_{м. г.}=_гН/Е_г=1,6716,8/0,104=270.

Приведенный критерий Пекле:

;

.

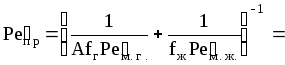
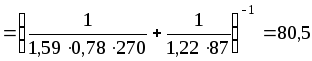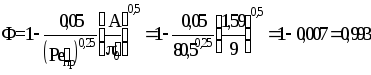Поправки на обратное перемешивание:

.

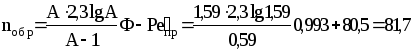
Число единиц переноса с учетом обратного перемешивания:

,

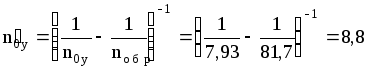что близко к значению n_0y=9, принятому в начале расчета.

* Коган В.Б. и др. Равновесие между жидкостью и паром. Кн 1,2/В.Б.Коагн, В.М.Фридман, В.В.Кафаров. – М.; Л.; Наука, 1966. 640-786 с.

 См., например, данные о равновесных концентрациях в табл. XLVII.

^ Иногда пишут или



 При расчете мольного объема химического соединения величину соответствующей структурной постоянной надо прибавить к сумме атомных объемов.

* Рамм В. М. Абсорбция газов.-М.: Химия, 1976. 655с.

* ^* Рамм В. М. Абсорбция газов.-М.: Химия, 1976. 655с.

5