6

Курс лекций “Математическое моделирование”

1. Модели и моделирование

Лекция 3

1.6. Классификация математических моделей

Лавинообразное развитие методов математического моделирования и многообразие областей их использования привели к появлению огромного количества моделей самого разного типа.

Математические модели разделяются на классы в зависимости:

• от сложности объекта моделирования;

• от оператора модели;

• от входных и выходных параметров;

• от цели моделирования;

• от метода исследования модели.

1.6.1. Классификация в зависимости от сложности объекта моделирования

В качестве объекта моделирования может выступать как некоторое материальное тело или конструкция, так и природный, технологический или социальный процесс или явление. Все объекты моделирования можно разделить на две группы: простые и объекты-системы (см. рис.1.9).

Рис. 1.9. Классификация объектов моделирования

Напомним, что система есть совокупность множества объектов с набором связей между ними и между их свойствами, в определенном смысле обособленная от окружающей среды и взаимодействующая с ней как целое.

Для сложных систем характерно наличие большого числа взаимно связанных, взаимодействующих между собой элементов. При этом связь между элементами и системы может отличаться от связи между элементами и . Если система имеет элементов, и каждый элемент связан с каждым, то общее число связей равно . Если все элементов имеют по состояний, то общее число состояний для такой системы равно . Например, для системы при и имеем состояний.

Максимальное число связей в подобной системе равно 6. Если поведение системы описывается процессом перехода из одного состояния в другое, то общее число сценариев возможного поведения системы равно . В нашем случае число сценариев возможного поведения системы равно 64.

Поведение системы быстро усложняется с ростом числа элементов системы. Так для системы из 10 элементов при число состояний , а число сценариев 1 048 576. Данное обстоятельство, с одной стороны, говорит о сложности систем и многовариантности их поведения. С другой стороны, следует ожидать наличия больших трудностей, возникающих при изучении и моделировании систем.

Деление объектов исследования на “простые” и “сложные” условно. Все зависит от уровня детализации объекта.

Модели объектов-систем, учитывающие свойства и поведение отдельных элементов, а также взаимосвязи между ними, называются структурными.

1.6.2. Классификация в зависимости от оператора модели

Классификация математических моделей в зависимости от вида оператора представлена на рис.1.10.

Рис. 1.10. Классификация в зависимости от оператора модели

Оператор модели может быть линейным и нелинейным, алгоритмом, или определяться совокупностью уравнений (алгебраических, обыкновенных дифференциальных уравнений (ОДУ), систем ОДУ (СОДУ), дифференциальных уравнений в частных производных (ДУЧП), интегродифференциальных уравнений (ИДУ) и др.)

Линейные модели более просты для анализа. Например, из свойств линейности следует свойство суперпозиции решений, т.е. если известны решения при и при , то решение для входных параметров есть . Предельные значения для линейных моделей достигаются, как правило, на границах областей допустимых значений входных параметров.

Линейное поведение свойственно относительно простым объектам. Системам, как правило, присуще нелинейное многовариантное поведение. Анализ подобных моделей намного сложнее.

В качестве примера простых моделей можно привести закон Гука, закон Ома, законы Ньютона и т.д.

В ряде случаев можно построить некий имитатор поведения и свойств объекта с помощью алгоритма не прибегая к математическим соотношениям. Например, если в результате наблюдения за объектом получена таблица соответствия между входными и выходными значениями параметров, то определить оператор зачастую бывает проще с помощью алгоритма.

1.6.3. Классификация в зависимости от параметров модели

Классификация моделей в зависимости от параметров модели представлена на рис. 1.11.

Рис. 1.11. Классификация в зависимости от параметров модели

В общем случае параметры, описывающие состояние и поведение объекта моделирования, разбиваются на ряд непересекающихся подмножеств:

• совокупность входных (управляемых) воздействий на объект ;

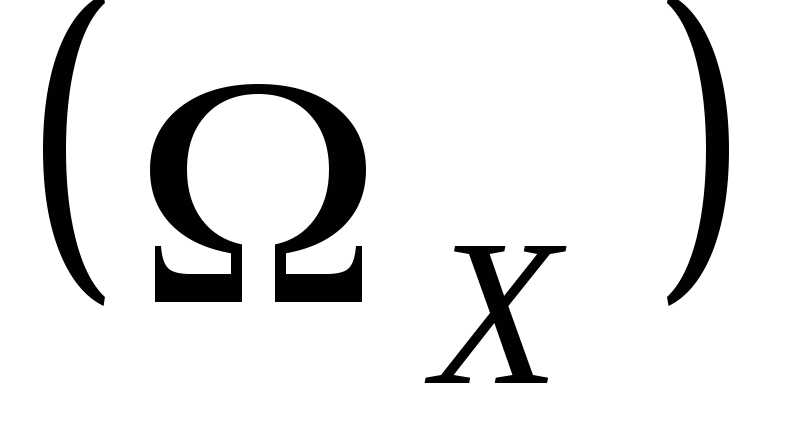• совокупность воздействий внешней среды (неуправляемых) ;

• совокупность внутренних (собственных) параметров объекта ;

• совокупность выходных характеристик .

Следует отметить, что количество параметров всех типов в математических моделях, как правило, конечно. При этом каждый из параметров может иметь различную математическую природу: быть постоянной величиной или функцией, скаляром или вектором (или тензором второго, третьего и т.д. ранга), четким или нечетким множеством и т.д.

По своей природе характеристики объекта могут быть как качественными, так и количественными. Кроме того, количественные значения параметра могут выражаться дискретными или непрерывными величинами. Качественные характеристики находятся, например, с помощью метода экспертных оценок.

При построении модели описание неопределенности параметров может быть осуществлено следующими способами:

1. детерминированное. Данный способ соответствует полной определенности всех параметров;

2. стохастическое – значение всех или отдельных параметров определяется случайными величинами, заданными плотностями вероятности;

3. случайное – значение всех или отдельных параметров устанавливаются случайными величинами, заданными оценками плотностей вероятности, полученными в результате обработки ограниченной экспериментальной выборки данных параметров. Данная форма описания тесно связана с предыдущей. Однако в данном случае получаемые результаты моделирования будут существенным образом зависеть от точности оценок моментов и плотностей вероятности случайных параметров, от постулируемых законов распределения, объема выборок;

4. интервальное – значение всех или отдельных параметров модели описываются интервальными величинами, заданным интервалом, образованным минимальным и максимально возможными значениями параметра;

5. нечеткое – значение всех или отдельных параметров модели описываются функциями принадлежности соответствующему нечеткому множеству. Такая форма используется, когда информация о параметрах модели задается экспертом на естественном языке, а следовательно, в “нечетких” (с позиции математики) терминах типа “много больше единицы”, “около нуля” и т. д.

Совокупность значений параметров модели в некоторый момент времени или на данной стадии называется состоянием объекта.

Если параметры модели не зависят от времени, то говорят, что такая модель является стационарной, и наоборот – нестационарной.

Разделение моделей на нульмерные, одномерные, двумерные и трехмерные применимо для моделей, в число параметров которых входят координаты пространства. С ростом размерности сложности реализации модели усложняется на порядки. Поэтому при разработке модели стараются (если это возможно) понизить размерность. Однако необоснованное понижение размерности модели может существенно исказить результаты моделирования. Например, если для исследования движения брошенного мяча в вертикальной плоскости использование двумерной модели может быть оправдано, то для исследования движения бумеранга двумерную модель строить бесполезно.