
- •1. Программирование.
- •1.1. Программное обеспечение. Основные этапы решения задач на эвм. Жизненный цикл программного средства
- •Каскадная модель.
- •1.2. Характеристика объектно-ориентированного программирования.
- •1.3. Использование инкапсуляции в ооп.
- •1.4. Использование наследования объектов в ооп.
- •1.5. Использование полиморфизма в ооп.
- •2. Математическая логика и теория алгоритмов.
- •2.1. Логические операции. Таблицы истинности.
- •2.2. Логика высказывани и предикатов.
- •Организация эвм и систем.
- •Принцип программного управления
- •Структуры вычислительных машин
- •Структуры вычислительных систем.
- •Cisc и risc процессоры
- •Иерархическая система памяти эвм. Общие сведения и классификация памяти эвм.
- •Классификация зу по принципу организации.
- •Вычислительные системы (вс). Уровни параллелизма. Классификация вс Флинна. Закон Амдала.
- •4. Операционные системы.
- •Классификация ос.
- •Средства синхронизации и взаимодействия процессов.
- •Файловая система.
- •Сегментно-страничное распределение памяти.
- •Страничное распределение памяти
- •Сегментное распределение памяти.
- •Сегментно-страничное распределение.
- •5. Базы данных.
- •База данных. Субд.
- •Реляционная модель данных.
- •Нормальные формы.
- •2) Вторая нормальная форма.
- •3) Третья нормальная форма.
- •Физическая организация данных.
- •6. Компьютерная графика.
- •Растровые (матричные) изображения.
- •Векторные модели изображений.
- •3D-изображения. Геометрия проецирования. Однородные координаты.
- •Представление геометрических моделей в программе и базе данных.
- •Графические библиотеки
- •Информационные технологии.
- •Информационная технология как составная часть информатики.
- •Базовая ит. Концептуальный уровень.
- •Структура базовой ит. Логический уровень.
- •Базовая ит. Физический уровень. Преобразование информации в данные.
- •Графические модели ит.
- •8. Сети эвм и телекоммуникации.
- •Структура и характеристики вычислительных сетей.
- •Топологии вычислительных сетей
- •Кольцо.
- •Архитектура сетей Ethernet.
- •Стандарт 10BaseT
- •Стандарт 10Base2
- •Стандарт 10Base5
- •8.4. Сети 802.11
- •Режимы работы 802.11
- •8.5. Сетевые операционные системы.
- •1. Программирование
2.2. Логика высказывани и предикатов.
Логическое высказывание – связанное повествовательное предложение, о котором можно сказать истинно оно или ложно (На улице идёт дождь – высказывание, какая хорошая погода – не высказывание). В логике высказываний нас интересует не содержание, а истинностное значение высказываний (0 – Ложь, 1 – Истина).
Высказывания
А и В равносильны тогда и только тогда,
когда истинностные значения А и В
совпадают (![]() ).
).
Основные операции над логическими высказываниями: (см. вопрос 2.1).
Логика предикатов –логическая система, средствами которой можно исследовать структуру высказываний.
Предикат – свойство объекта (отношения между объектами). Быть чётным, быть простым, делиться, быть больше.
![]() – унарный.
– унарный.
![]() – бинарный.
– бинарный.
![]() – трёхместный.
– трёхместный.
Предикат
– функция, высказывательные переменные
которой принимают значения из некоторого
множества ![]() ,
а сама функция принимает значения {0;
1}.
,
а сама функция принимает значения {0;
1}.
![]()
Для задания предиката должно быть задано:
Область определения
 ,
состоящая из множества предметных
переменных.
,
состоящая из множества предметных
переменных.Множество
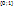 – область значений предиката.
– область значений предиката.Правило, по которому каждому элементу из множества
 ставится в соответствие элемент из
множества
ставится в соответствие элемент из
множества  .
.
Способы задания предиката.
Графический.

![]()
![]()
![]()
![]()
![]()
Табличный
1
2
4
5

1
0
0
0
Словесный
Предикат
![]() выполняется при
выполняется при ![]() и не выполняется во всех остальных
точках x
области определения и не выполняется
при n
= 2,4,5.
и не выполняется во всех остальных
точках x
области определения и не выполняется
при n
= 2,4,5.
Формульный (аналитический).
![]()
![]()
![]()
В логике предикатов для образования предложений можно использовать те же логические операции, что и в логике высказываний, т.е. дизъюнкцию, конъюнкцию, эквиваленцию, в результате получаются новые предикаты.
![]()
![]()
![]()
Кванторы.
Квантор общности.
 .
Пусть
.
Пусть 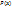 –некоторый
предикат, под выражением
–некоторый
предикат, под выражением  будем подразумевать высказывание,
истинное когда
будем подразумевать высказывание,
истинное когда  истина для любого
истина для любого  из множества
из множества  и
ложное в противоположном случае.
и
ложное в противоположном случае.Квантор существования.
 .
Пусть
.
Пусть  –некоторый
предикат, под выражением
–некоторый
предикат, под выражением  будем подразумевать высказывание,
истинное когдасуществует элемент из
множества
будем подразумевать высказывание,
истинное когдасуществует элемент из
множества  ,
для которого
,
для которого  истинно и ложное в противоположном
случае.
истинно и ложное в противоположном
случае. .
Существует
такое x,
которое кратно 2 и кратно 3.
.
Существует
такое x,
которое кратно 2 и кратно 3.
Операции, уменьшающие местность предиката.
Фиксация значений переменной.
![]()
![]()
![]()
![]()
Операция связывания квантором
![]()
![]()
![]()
![]()
Обобщение логических операций с помощью квантора.
Пусть
![]() – одноместный предикат, который определён
на конечном множестве
– одноместный предикат, который определён
на конечном множестве ![]() .
.
![]() .
Квантор общности определяет операцию
конъюнкция.
.
Квантор общности определяет операцию
конъюнкция.
Квантор существования обобщает операцию дизъюнкция.
Основные равносильности алгебры предикатов, содержащие кванторы.
Законы де Моргана.
 ,
,
 (перенос отрицания).
(перенос отрицания).Перестановка одноимённых кванторов (коммунитативные законы).
 ,
,
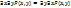 .
.Дистрибутивные законы.
 ,
,

Законы ограничения действия кванторов
 ,
,
 ,
,
 ,
,
 .
.
Все законы, которые работают в алгебре высказываний, переносятся в алгебру предикатов.
ИНТУИТИВНОЕ И ФОРМАЛЬНОЕ ОПРЕДЕЛЕНИЕ АЛГОРИТМА.
Алгоритм – эффективная процедура, однозначно приводящая к результату.
Основные требования к алгоритму: 1. Каждый алгоритм должен иметь данные: входные, выходные и промежуточные; 2. Данные для своего размещения требуют внутреннюю и внешнюю память; 3. Алгоритм состоит из отдельных элементарных шагов количество, которое конечное; 4. Последовательность шагов алгоритма детерминировано, то есть после каждого шага либо указывается какой шаг делать дальше либо дается команда остановки; 5. Результативность – остановка после конечного числа шагов с указанием того что считать результатом.
Алгоритмическая модель – формализация понятия алгоритма. Она является универсальной, то есть допускается описание любых алгоритмов. Выделяют 3 основных типа алгоритмической модели:1. Рекурсивные функции – вычисление и числовые функции; 2. Машина Тьюринга – прообраз современной ЭВМ. В основе лежит представление, а в алгоритме как в некотором детерминированном устройстве способном выполнять в каждый отдельный момент времени лишь примитивные операции; 3. Каноническая система Поста и нормальные алгоритмы Маркова. Преобразование слов в произвольных алфавитах в кот. элементарные операции это подстановки, то есть замены части слова другим словом.
Машина Тьюринга представляет собой автомат, с конечным числом состояний, соединенный с внешней памятью – лентой, разбитой на ячейки, в каждой из которых записан один из символов конечного алфавита А= { a1, ... am}. Автомат связан с лентой с помощью головки, которая в каждый момент времени обозревает одну ячейку ленты, и в зависимости от символа в этой ячейке и состояния управляющего устройства записывает в ячейку символ (совпадающий с прежним или пустой), сдвигается на ячейку вправо или влево или остается на месте. Среди состояний управляющего устройства выделим начальное состояние q1 и заключительное состояние qz. В начальном состоянии машина находится перед началом работы. Попав в заключительное состояние, машина останавливается. Т.о. память машины Т – это конечное множество состояний (внутренняя память) и лента (внешняя память). Лента бесконечна в обе стороны, однако в любой момент времени лишь конечный отрезок ленты будет заполнен символами. Поэтому важна не фактическая бесконечность ленты, а ее неограниченность, т.е. возможность писать на ней сколь угодно длинные, но конечные слова.
Данные в машине Т – это слова в алфавите ленты; на ленте записываются и исходные данные и окончательные результаты. Элементарные шаги – это считывание и запись символов, сдвиг головки на ячейку влево или вправо, а также переход управляющего устройства в следующее состояние.
Детерминированность машины Т определяется следующим образом: для любого внутреннего состояния qi и символа aj однозначно заданы
а) следующее состояние qi`
б) символ aj`, который надо записать в ту же ячейку вместо aj (стирание – это запись пустого символа )
в) направление сдвига головки dk (L – влево, R – вправо, E – на месте).
Это задание может описываться либо системой правил
qi aj qi` aj` dk
либо таблицей, строкам которой соответствуют состояния, столбцам – входные символы, а на пересечении записана тройка символов qi` aj` dk.
либо блок-схемой (диаграммой переходов), в которой состояниям соответствуют вершины, а правилу вида (qi aj qi` aj` dk) – ребро, ведущее из qi в qi` .
ТЕОРИЯ СЛОЖНОСТИ В ТЕОРИИ АЛГОРИТМОВ.
Алгоритм имеет сложность O(f(n)), если при увеличении размерности входных данных N, время выполнения алгоритма возрастает с той же скоростью, что и функция f(N).
функции, которые чаще всего используются для вычисления сложности. Функции перечислены в порядке возрастания сложности. Чем выше в этом списке находится функция, тем быстрее будет выполняться алгоритм с такой оценкой. 1. C – константа 2. log(log(N)) 3. log(N) 4. N^C, 0<C<1 5. N 6. N*log(N) 7. N^C, C>1 8. C^N, C>1 9. N! Самый трудоемкий. Если мы хотим оценить сложность алгоритма, уравнение сложности которого содержит несколько этих функций, то уравнение можно сократить до функции, расположенной ниже в таблице. Например, O(log(N)+N!)=O(N!). Если алгоритм вызывается редко и для небольших объёмов данных, то приемлемой можно считать сложность O(N^2), если же алгоритм работает в реальном времени, то не всегда достаточно производительности O(N). Обычно алгоритмы со сложностью N*log(N) работают с хорошей скоростью. Алгоритмы со сложностью N^C можно использовать только при небольших значениях C. Вычислительная сложность алгоритмов, порядок которых определяется функциями C^N и N! очень велика, поэтому такие алгоритмы могут использоваться только для обработки небольшого объёма данных.
Классы сложности.
1. Класс P – задачи, которые могут быть решены за время, полиномиально зависящее от объёма исходных данных, с помощью детерминированной вычислительной машины (например, машины Тьюринга),
2. Класс NP — задачи, которые могут быть решены за полиномиально выраженное время с помощью недетерминированной вычислительной машины, то есть машины, следующее состояние которой не всегда однозначно определяется предыдущими. К классу NP относятся задачи, решение которых с помощью дополнительной информации полиномиальной длины, данной нам свыше, мы можем проверить за полиномиальное время. В частности, к классу NP относятся все задачи, решение которых можно проверить за полиномиальное время. Класс P содержится в классе NP. Классическим примером NP-задачи является задача о коммивояжёре.
Работу такой машины можно представить как разветвляющийся на каждой неоднозначности процесс: задача считается решённой, если хотя бы одна ветвь процесса пришла к ответу.
Поскольку класс P содержится в классе NP, принадлежность той или иной задачи к классу NP зачастую отражает наше текущее представление о способах решения данной задачи и носит неокончательный характер. В общем случае нет оснований полагать, что для той или иной NP-задачи не может быть найдено P-решение. Вопрос о возможной эквивалентности классов P и NP (то есть о возможности нахождения P-решения для любой NP-задачи) считается многими одним из основных вопросов современной теории сложности алгоритмов. Ответа на этот вопрос нет. Сама постановка вопроса об эквивалентности классов P и NP возможна благодаря введению понятия NP-полных задач. NP-полные задачи составляют подмножество NP-задач и отличаются тем свойством, что все NP-задачи могут быть тем или иным способом сведены к ним. Из этого следует, что если для NP-полной задачи будет найдено P-решение, то P-решение будет найдено для всех задач класса NP. Примером NP-полной задачи является задача о конъюнктивной форме.
