
Дискретка_Экзамен_Ответы / комб / 2 Теоремы о количестве комбинаторных объектов
..docxТеорема 2.1. Количество всех различных подмножеств n-элементно-го множества равно 2n.
Доказательство. Поставим в соответствие каждому подмножеству А множества В n-разрядный двоичный вектор, i-ый разряд которого равен единице только тогда, когда i-ый элемент множества В принадлежит подмножеству А. Для того, чтобы сформировать n-разрядный двоичный вектор, нужно выполнить одно за другим n действий: заполнить 1-ый разряд вектора, 2-ой разряд и так до n-го разряда. Каждое действие можно выполнить двумя способами (разряд двоичного вектора можно заполнить только нулём или единицей). По правилу произведения все n действий могут быть выполнены 22…2=2n способами, т.е. может быть получено 2n различных n-разрядных двоичных векторов, следовательно, количество всех различных подмножеств n-элементного множества равно 2n.
Теорема 2.2. Количество всех различных перестановок n-элемент-ного множества М (количество способов упорядочивания множества) определяется формулой Рn=n!.
Доказательство. Перестановку можно представить последовательностью из n мест. Для того чтобы получить одну перестановку, нужно выполнить одно за другим n действий: заполнить 1-ое место в последовательности, 2-ое место и так до n-го места. Для выполнения 1-го действия (заполнения 1-го места) можно взять любой элемент из множества М и поставить его на 1-ое место, т.е. его можно выполнить n-способами, и после этого в множестве М останется n-1 элемент. Для выполнения 2-го действия (заполнения 2-го места) можно взять любой элемент из оставшихся в множестве М и поставить его на 2-ое место, т.е. его можно выполнить n-1-способами, и после этого в множестве М останется n-2 элемента и т.д. По правилу произведения все n действий могут быть выполнены n(n-1)(n-2)...21=n! способами, следовательно, количество всех различных перестановок n-элементного множества равно n!.
Теорема 2.3. Количество всех различных размещений n-элементного множества М по k местам определяется формулой
 .
.
Доказательство. Размещение можно представить последовательностью из k мест. Для того чтобы получить одно размещение, нужно выполнить одно за другим k действий: заполнить 1-ое место в последовательности, 2-ое место и так до k-го места. Для выполнения 1-го действия (заполнения 1-го места) можно взять любой элемент из множества М и поставить его на 1-ое место, т.е. его можно выполнить n-способами, и после этого в множестве М останется n-1 элемент. Для выполнения 2-го действия (заполнения 2-го места) можно взять любой элемент из оставшихся в множестве М и поставить его на 2-ое место, т.е. его можно выполнить n-1-способами, и после этого в множестве М останется n-2 элемента и т.д. до k-го места. По правилу произведения все k действий могут быть выполнены
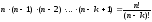 способами,
следовательно,
количество всех различных размещений
n-элементного
множества М по k
местам равно
способами,
следовательно,
количество всех различных размещений
n-элементного
множества М по k
местам равно
 .
.
Теорема 2.4. Количество всех различных размещений с повторениями n-элементного множества М по k местам равно nk.
Доказательство. Для того чтобы получить одно размещение с повторениями, нужно выполнить одно за другим k действий: заполнить 1-ое место в последовательности, 2-ое место и так до k-го места. Для выполнения каждого действия можно взять любой элемент из множества М и поставить его на соответствующее место, т.е. каждое из k действий можно выполнить n способами. По правилу произведения все k действий могут быть выполнены nn…n=nk способами, следовательно, количество всех различных размещений с повторениями n-элементного множества по k местам равно nk.
Теорема
2.5. Количество
всех различных сочетаний из n
элементов по k
определяется формулой
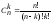 .
.
Доказательство.
Можно получить все
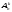 размещений,
упорядочив всеми возможными способами
каждое из
размещений,
упорядочив всеми возможными способами
каждое из
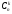 сочетаний. Количество способов
упорядочивания одного сочетания равно
k!,
следовательно
сочетаний. Количество способов
упорядочивания одного сочетания равно
k!,
следовательно
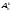 =
=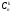 k!
. Отсюда
k!
. Отсюда
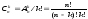 .
.
Теорема
2.6.
Число перестановок с повторениями для
мультимножества S={n1*s1,n2*s2,...,nk*sk}
выражается формулой
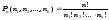 ,
где
,
где
 .
.
Доказательство. Рассмотрим одну перестановку мультимножества и заменим в ней все одинаковые элементы разными. Тогда, число различных перестановок, которые можно составить из рассматриваемой, равно n1!n2!…nk!. Проделав это для каждой перестановки, получим n! перестановок. Следовательно, Pn(n1,n2,…,nk)n1!n2!…nk!=n!. Отсюда
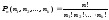
Теорема
2.7. Количество
различных сочетаний из n
элементов по k
с повторениями равно
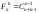 .
.
Доказательство. Каждое сочетание полностью определяется, если указать, сколько раз входит каждый элемент множества в сочетание. Поставим в соответствие каждому сочетанию последовательность нулей и единиц, составленную по следующему правилу: ставим подряд столько единиц, сколько раз входит первый элемент множества в сочетание, далее ставим нуль, и после него пишем столько единиц, сколько раз входит первый элемент множества в это сочетание и т.д. Например, написанным выше сочетаниям из трех элементов по два будут соответствовать такие последовательности:
1100, 1010, 1001, 0110, 0101, 0011.
Таким
образом, каждому сочетанию с повторениями
из n
по k
соответствует последовательность из
k
единиц и n-1
нулей. Количество таких последовательностей
равно числу способов, которыми можно
выбрать n-1
мест для нулей из n+k-1
общего числа мест (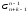 ),
или, то же самое, - числу способов выбора
k
мест для единиц из n+k-1
мест (
),
или, то же самое, - числу способов выбора
k
мест для единиц из n+k-1
мест ( ).
).
