
Дискретка_Экзамен_Ответы / мн-ва / 1 Методы доказательства теоретико-множественных тождеств
.docx1.5. Методы доказательства теоретико-множественных тождеств
Равенство, левая и правая части которого представляют собой выражения в алгебре подмножеств, верное для любых входящих в них множеств, называют теоретико-множественным тождеством . Рассмотрим различные методы доказательства теоретико-множественных тождеств.
1.5.1. Метод двух включений
Пусть левая часть теоретико-множественного тождества определяет множество X , а правая часть – множество Y . Чтобы доказать равенство множеств X и Y , достаточно доказать два включения XY и YX , т.е. доказать, что из предположения xX (для произвольного x) следует, что xY , и, наоборот, из предположения xY следует, что xX.
Докажем этим методом тождество:
АВ = (АВ)-(АВ).
Пусть xАВ. Тогда, согласно определению симметрической разности, x(A-B)(B-A). Это означает, что x(A-B) или x(В-А). Если x(A-B), то хА и хВ, т.е. хАB и при этом хАВ. Если же х(В\А), то хВ и хА, откуда хАB и хАВ. Итак, в любом случае из х(А-В)(В-А) следует хАB и хАВ, т.е. и х(АВ)- (АВ). Таким образом, доказано, что
АВ (АВ)-(АВ).
Покажем обратное включение (АВ)-(АВ) АВ.
Пусть х(АВ)-(АВ). Тогда хАВ и хАВ. Из хАВ следует, что хА или хВ. Если хА, то с учетом хАВ имеем хВ, и поэтому хА-В. Если же хВ, то опять-таки в силу хАВ получаем, что хА и хВ-А. Итак, хА-В или хВ-А, т.е. х(А-В) (В-А). Следовательно,
(АВ)-(АВ) АВ.
Оба включения имеют место и тождество доказано.
1.5.2. Метод эквивалентных преобразований
Теоретико-множественные тождества можно доказывать, используя свойства операций над множествами. Для этого нужно преобразовать левую часть в правую, или правую – в левую, или правую и левую часть в некоторое третье выражение.
Докажем этим методом тождество:
(AB)(AC)= A(BC).
Преобразуем левую часть к правой:
(AB)(AC)=((AB)(AC))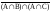 =(A(BC))(
=(A(BC))(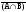
 )=(A(BC))(
)=(A(BC))(
 )
(
)
(
 )==(A(BC))(
(
)==(A(BC))(
( (
(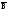
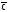 ))=((A(BC))
))=((A(BC)) )((A(BC))(
)((A(BC))(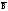
 ))
= ((A(BC))
(A(
))
= ((A(BC))
(A(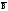
 ))=(A(BC))
(A
))=(A(BC))
(A )=
)=
= A((BC)
 )=
A((BC)-(BC))=
A(BC).
)=
A((BC)-(BC))=
A(BC).
1.5.3. Метод характеристических функций
Характеристическая функция А множества А для хU определяется следующим образом: А(x)=1, если xA и А(x)=0, если xA.
Для характеристической функции А множества А справедливо тождество:
А2(x)=А(x).
АВ(x)= А(x)*В(x).
АВ(x)= А(x)+В(x)-А(x)*В(x).
 (х)=1-А(x).
(х)=1-А(x).
А-В(x)= А(x)-А(x)*В(x),
АВ(x)= А(x)+В(x)-2*А(x)*В(x).
Докажем этим методом тождество:
(AB)C=(AC)(BC).
C одной стороны,
(AB)C(х)=(AB)(х)*C(х)=(A(х)+В(х)-2*A(х)*В(х))*С(х)=A(х)*С(х)+В(х)*С(х)-2*A(х)*В(х)*С(х).
С другой стороны,
(AC)(BC)(x)=AC(x)+BC(x)-2*AC(x)*BC(x)=A(x)*C(x)+B(x)*C(x)-2*A(x)*C(x)*B(x)*C(x)=
=A(x)*C(x)+B(x)*C(x)-2*A(x)*B(x)*C(x).
1.5.4. Метод логических функций
В результате выполнения операций объединения, пересечения, разности, симметрической разности и дополнения из исходных множеств получаем новые множества, которые определяются следующим образом (см. п.1.3.“Операции над множествами“):
АВ = {x | xA или xB}
АВ = {x | xA и xB}
А-В = {x | xA и xB}
АВ = {x | xA и xB или xВ и xА}
 = {x
| xА}
= {x
| xА}
Из этих определений с учётом того, что xА = не xA , следует справедливость следующих равенств:
xАВ = xA или xB
xАВ = xA и xB
xА-В = xA и не xB
xАВ = xA и не xB или xВ и не xА
x = не xА
= не xА
Если полученные функции имеют одну и туже таблицу истинности, то тождество верно.
Докажем этим методом тождество:
(AB)C=(AC)(BC).
Для левой части,
x((AB)C) = x(AB) и xC = (xA и не xB или xВ и не xА) и xC
Для правой части,
x(AC)(BC) = x AC и не xBC или xВC и не xAC =
= xA и xС и не (xВ и xС) или xВ и xС и не (xA и xB)
Логические функции для левой и правой части тождества получены и их таблицы истинности (табл.1.2) совпадают, следовательно, тождество верно.
Таблица 1.2
Таблица истинности
|
XА |
xВ |
xС |
Левая часть |
Правая часть |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
1.5.5. Теоретико-множественный метод
Этот метод основан на вычислении теоретико-множественного тождества при определённых значениях входящих в него множеств, и, если при этих значениях множеств теоретико-множественное тождество истинно, то оно истинно и при любых других значениях входящих в него множеств.
Пусть теоретико-множественное тождество содержит n исходных множеств А1,А2, … ,Аn и каждая пара множеств находится в общем положении. Тогда универсум разбивается на множество В={В1,В2, … ,Вm} попарно-непересекающихся подмножеств. Каждому подмножеству Вj можно поставить в соответствие n-разрядный двоичный вектор, в котором i-ый разряд равен 1, если хотя бы один элемент множества Аi принадлежит подмножеству Вj , иначе i-ый разряд равен 0. Следовательно, количество m подмножеств, на которые разбивается универсум, равно количеству двоичных n-разрядных векторов, т.е. m=2n .
Определим множество Аi как множество, содержащее в себе в качестве элементов элементы множества В, объединение которых равно множеству Аi . Элемент ВjB будет принадлежать множеству Аi, если двоичный код числа j содержит единицу в i-ом разряде. Обозначим множество Bj натуральным числом j , тогда множество Аi будет представлять собой конечное множество натуральных чисел. Таким образом определим значения множеств А1,А2, … ,Аn и подставим их в левую и правую части тождества вместо исходных множеств А1,А2, … ,Аn . Вычислим множества, определяемые левой и правой частью тождества, и, если эти множества окажутся равными, то тождество верно.
Докажем этим методом тождество:
(AB)C=(AC)(BC).
Тождество содержит три исходных множества А, В и С, которые, в общем случае, разбивают универсум на 23 подмножеств, соответствующих 3-х разрядным двоичным векторам. В таблице 1.3 представлены двоичные вектора и соответствующие им номера подмножеств.
Находим значения множеств А, В и С.
Просматривая столбец таблицы 1.3, соответствующий множеству А, обнаруживаем единицы в строках, соответствующих подмножествам 1, 3, 5 и 7, т.е. А={1,3,5,7}. Аналогичным образом определяем значения множеств В и С: В={2,3,6,7}, С={4,5,6,7}.
Таблица 1.3
Разбиение универсума множествами А, В и С на подмножества
|
Исходные множества |
Номер Подмножества |
|||
|
С |
В |
А |
||
|
0 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
2 |
|
|
0 |
1 |
1 |
3 |
|
|
1 |
0 |
0 |
4 |
|
|
1 |
0 |
1 |
5 |
|
|
1 |
1 |
0 |
6 |
|
|
1 |
1 |
1 |
7 |
|
Разбиение универсума множествами А, В и С на подмножества показано на рис.1.2 с помощью кругов Эйлера.

А 1 3 2 В
5 7 6
0
4 С
Рис.1.2. Разбиение универсума множествами А, В и С
на подмножества
Далее в левую и правую части тождества вместо исходных множеств А, В и С подставляем значения множеств А, В и С:
левая часть
(AB)C=({1,3,5,7}{2,3,6,7}){4,5,6,7}= {1,5,2,6}{4,5,6,7}={5,6}
правая часть
(AC)(BC)= ({1,3,5,7}{4,5,6,7})({2,3,6,7}{4,5,6,7})={5,7}{6,7}={5,6}
Значения левой и правой части совпадают, следовательно, тождество верно.
