1.1.13. Эквипотенциальные поверхности

Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение эквипотенциальной поверхности.:.При перемещении по эквипотенциальной поверхности на отрезок потенциал не изменяется. Таким образом, касательная к поверхности составляющая вектораравна нулю. Тогда векторнаправлен по нормали к эквипотенциальной поверхности в каждой ее точке, а линии напряженности в каждой точке перпендикулярны к эквипотенциальным поверхностям.

Если эквипотенциальные поверхности построить таким образом, чтобы разность потенциалов для двух соседних поверхностей была одна и та же, то по густоте эквипотенциальных поверхностей можно судить о напряженности поля. Действительно, чем гуще эквипотенциальные поверхности, тем больше , тем больше.

Для однородного поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению поля.

Рассмотрим эквипотенциальную поверхность точечного заряда. Потенциал точечного заряда (рис.1.1.19) равен . Таким образом, эквипотенциальная поверхность этого заряда будет сферой радиусас центром в точке заряда. Силовые же линии, как мы установили ранее, расходятся радиально от заряда если он положительный, или сходятся к заряду, если онотрицательный. То есть векторперпендикулярен эквипотенциальным поверхностям.

Лекция 2

1.2. Диэлектрики в электрическом поле

1.2.1.Полярные и неполярные молекулы

Если диэлектрик внести в электрическое поле, то и поле, и диэлектрик претерпевают изменения. В составе атомов и молекул имеются положительные и отрицательные заряды (ядра, электроны). Электроны движутся в пределах атома или молекулы с огромной скоростью, их положения меняются, и действие каждого электрона на заряды будет таким, как если бы он находился в покое в некоторой точке, которая является усредненным положением электронов во времени.

Если расстояния превышают размеры молекулы, то действие всех электронов молекулы эквивалентно действию суммарного заряда, помещенного в некоторую точку внутри молекулы. Эта точка называется центром тяжести отрицательных зарядов, Действие же ядер эквивалентно действию их суммарного заряда, по­мещенного в центр тяжести положительных зарядов. Ясно, что центр положительных зарядов определяется радиус-вектором:

,

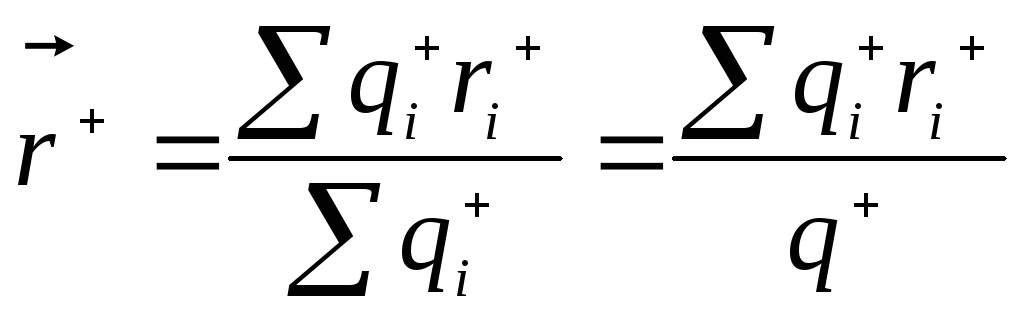где - радиус-вектор точки, в которой появляется-ый положительный заряд- суммарный положительный заряд молекулы.

Радиус-вектор центра тяжести отрицательных зарядов равен:

.

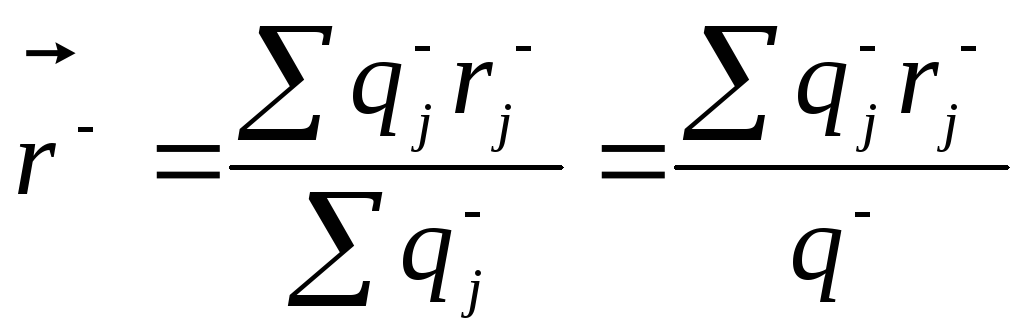Ясно, что суммарный положительный заряд молекулы равен суммарному отрицательному заряду, взятому с обратным знаком.

В отсутствие внешнего электрического поля центры положительных и отрицательных зарядов могут совпадать (молекула неполярна), либо не совпадать (молекула полярна, эквивалентна электрическому диполю). Полярная молекула обладает собственным электрическим моментом.

.

Если для положительных и отрицательных зарядов применить единую нумерацию, то

. (1.2.1)

Если система зарядов в целом нейтральна, то выражение (1.2.1) не зависит от выбора точки, относительно которой берутся радиус-векторы. Неполярные молекулы собственным электрическим моментом не обладают. Под действием внешнего электрического поля заряды в неполярной молекуле смещаются друг относительно друга: положительные по направлению поля, отрицательные - против поля. В результате молекула приобретает электрический момент, пропорциональный напряженности поля:

где - поляризуемость молекулы.

Явление, заключающееся в возникновении в каждом объеме диэлектрика макроскопического электрического дипольного момента, называется поляризацией.

Процесс поляризации неполярной молекулы можно объяснить, если представить, что положи­тельные и отрицательные заряды молекулы связаны друг другом силами, пропорциональными их смещению, то есть неполярная: молекула ведет себя как упругий диполь.

Действие внешнего поля на полярную молекулу сводится к стремлению повернуть молекулу так, чтобы ее электрический момент установился по направлению поля. На величину же электрического момента внешнее поле практически не влияет, то есть молекула ведет себя как жесткий диполь.