1.1.4.Принцип суперпозиции электрических полей

Основная задача электростатики заключается в том, чтобы по заданному распределению в пространстве и величине источников поля – электрических зарядов, найти величину и направление вектора напряженности в каждой точке поля.

Рассмотрим поле, созданное системой точечных зарядов . В механике рассматривался принцип независимости действия сил. Согласно этому принципу, результирующая сила, действующая со стороны исследуемого поля на пробный заряд, равна векторной сумме сил, приложенных к нему со стороны каждого из зарядов

. (1.1.1)

Однако известно, что ; и, где- напряженность результирующего поля;- напряженность поля, создаваемого одним зарядом. Тогда(выражение (1.1.1) разделили на) -напряженность электрического поля системы точечных зарядов равна векторной сумме напряженностей полей, создаваемых каждым из этих зарядов в отдельности.

Таким образом, результирующее поле можно найти простым наложением (суперпозицией) полей отдельных зарядов. В этом и состоит принцип суперпозиции полей, или принцип независимых действий электрических полей.

Пусть - радиус-вектор, проведенный из точечного зарядав исследуемую точку поля. Тогда напряженность, создаваемая этим зарядом в данной точке поля, а результирующая напряженность.

Каждое заряженное тело можно разбить на столь малые части, что каждая из них будет представлять собой точечный заряд. Поэтому формула эта пригодна для расчета любых электрических полей.

1.1.5. Примеры расчета полей на основе принципа суперпозиции. Электрическое поле диполя

Электрическим диполем называется система равных по величине и противоположных по знаку электрических зарядов и, расстояниемежду которыми мало по сравнению с расстоянием до рассматриваемых точек поля.

Молекулы диэлектриков по своим свойствам подобны диполям.

Плечом диполя называется вектор , направленный по оси диполя от отрицательного заряда к положительному и численно равен расстоянию между ними.Произведение положительного заряда диполя на плечо называется электрическим моментом диполя :.

Вектор совпадает по направлению с плечом диполя .

Согласно с принципом суперпозиции полей напряженность в произвольной точке диполя равна, гдеи- напряженности полей зарядовисоответственно.

1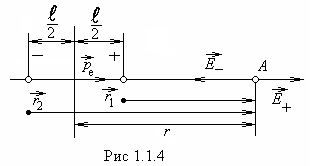.Если точкарасположена на оси диполя (рис.1.1.4), то векторыинаправлены вдоль этой оси в противоположные стороны,

, ,

где и- радиус-векторы, проведенные в точкуиз концов диполяи,;. Векторыисовпадают по направлению с, поэтому;, тогда,,

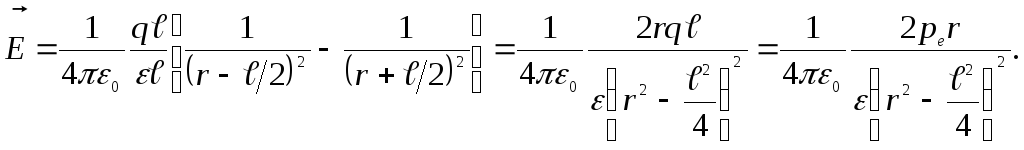
Если , то.

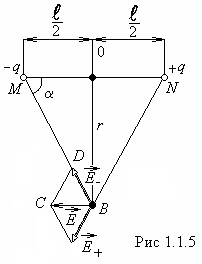
2. Найдем напряженность поля диполя в точке , расположенной на перпендикуляре, восстановленном к оси диполя из его середины(рис.1.1.5.). Точкаравноудалена от зарядови, поэтому:

Из подобных треугольников иполучаем, что векторантипараллелен вектору электрического момента диполя : Модуль напряженности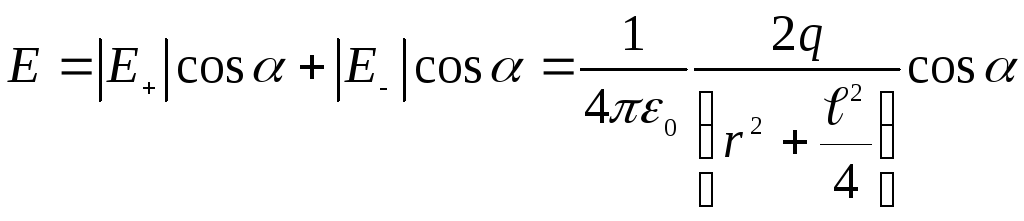, ясно, что,.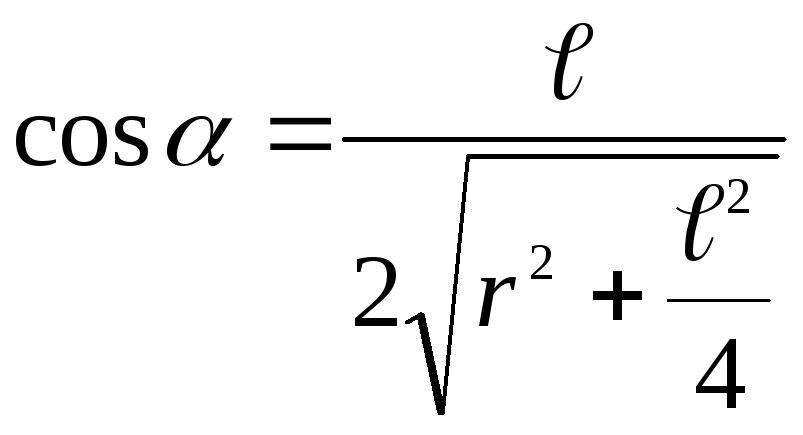

Тогда 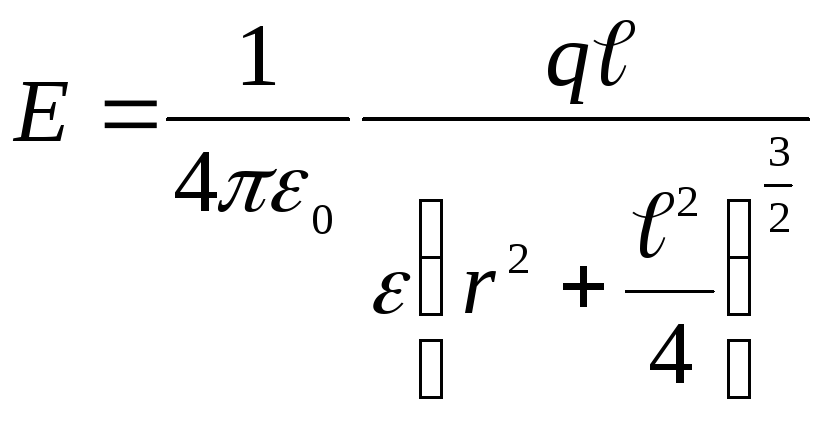. Величина, ею можно пренебречь, поэтому.

3. В общем случае пусть точка лежит на расстоянии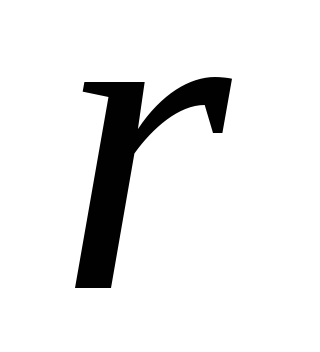от серединыдиполя, радиус-вектор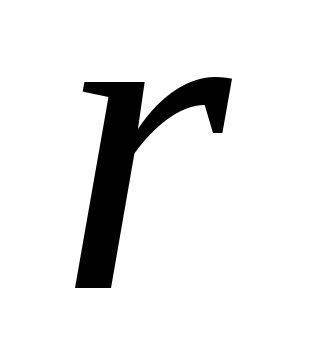образует с осью диполя угол(рис.1.1.6).

Опустим из точки перпендикулярна. Поместим в точкудва точечных зарядаи(равных по величине зарядам диполя). Этизаряды компенсируют друг друга и не искажают поле диполя. Четыре заряда, находящихся в точках можно рассматривать как два диполяи,, поэтому. Поэтому электрические моменты диполей соответственно равны:

; .

Для диполя точкалежит на его оси, напряженность, создаваемая этим диполем в точкеС равна .

Для диполя точкалежит на перпендикуляре, напряженность поля этого диполя.

Векторы ивзаимно перпендикулярны, поэтому результирующая напряженность равна:

Таким образом, напряженность электростатического поля диполя зависит от направления радиус-вектора относительно оси диполя и убывает пропорционально кубу расстоянияот его центра, то есть значительно быстрее, чем в случае поля одного точечного заряда.