Математика / Методические указания по теме Комплексные числа

Министерство образования Российской Федерации

Байкальский государственный университет экономики и права

Читинский институт

Кафедра математики

Методические указания к

расчетно-графической работе

по теме

«Комплексные числа»

для студентов 1-го курса

Чита 2010г.

Введение

Методические указания предназначены для студентов 1 курса финансово-информационного и экономического факультетов. Расчетно-графическая работа по теме «Комплексные числа» содержит 28 однотипных вариантов, каждый из которых состоит из 3 задач.

Первая задача предназначена для закрепления материала относительно алгебраической и тригонометрической формы комплексного числа, сопряженных комплексных чисел, корня третьей степени из комплексного числа и их графическому представлению.

Вторая задача углубляет понимание модуля комплексного числа, демонстрирует способ алгебраического и графического решения неравенств с комплексными числами.

Третья задача посвящена основным операциям с комплексными числами. Особое внимание уделено сопоставлению результатов, полученных в алгебраической и тригонометрической формах.

Для каждой задачи подробно рассмотрен пример решения, содержащий как необходимый теоретический материал, так и комментарии, акцентирующие внимание на основных элементах решения, где чаще всего студенты делают ошибки.

Демонстрационный вариант

Задача №1. Даны в алгебраической форме два числа и :

а) Найти алгебраическую форму числа ;

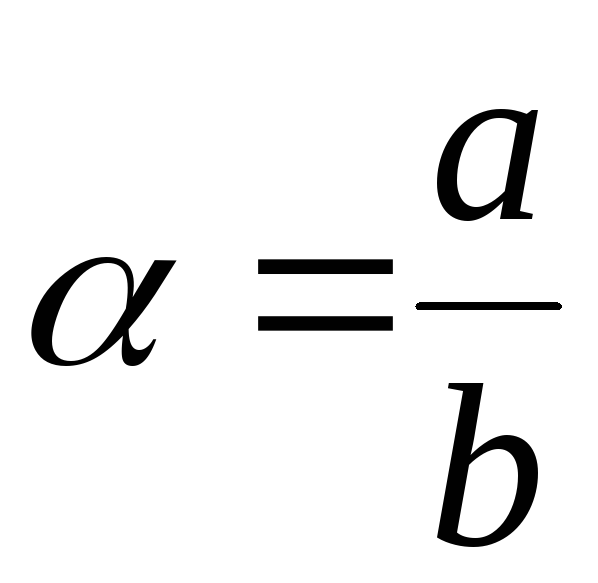б) Найти тригонометрическую форму числа ;

в) Решить уравнение ;

г) Изобразить числа , и полученные корни уравнения точками на комплексной плоскости.

,

Решение.

а) Комплексные числа , заданы в алгебраической форме, где – мнимая единица.

Если комплексное число задано в алгебраической форме , то число называется действительной частью комплексного числа, – мнимой частью, число – коэффициентом при мнимой части.

Определение. Два комплексных числа в алгебраической форме называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.

Например, для числа сопряженным является число . При делении комплексных чисел в алгебраической форме числитель и знаменатель дроби необходимо умножить на сопряженное число знаменателя. В результате в знаменателе исчезнет мнимая единица, при этом надо иметь в виду, что . В полученном выражении приводим подобные и получаем искомое комплексное число .

Ответ:

Замечание. Если в Вашем варианте попались числа, например, вида или , то их можно представить в виде или и дальше выполнять действия по предложенному выше шаблону.

б) Комплексное число в тригонометрической форме имеет вид:

,

где – модуль комплексного числа , – аргумент комплексного числа.

Если комплексное число задано в алгебраической форме , то модуль комплексного числа находят по формуле , а аргумент комплексного числа из выражений , .

В нашем примере , т.е. , , следовательно, модуль .

Выражения , выполняются для , .

Таким образом, комплексное число в тригонометрической форме имеет вид:

Так как , , то принято тригонометрическую форму комплексного числа записывать без , при этом угол называют главной частью аргумента комплексного числа. Итак, искомая тригонометрическая форма комплексного числа имеет вид:

в) Решим уравнение , где – комплексное число. Из уравнения имеем . Для возведения комплексного числа в ‑ую степень используется формула Муавра: .

Из пункта а) имеем , следовательно, . Представим число в тригонометрической форме аналогично пункту б):

,

, , , .

Отсюда, .

Замечание. Обратите внимание, что если , то . Числа и имеют одинаковый модуль, но разные аргументы, которые отличаются друг от друга на величину угла , что соответствует изменению направления радиус-вектора комплексного числа на противоположное, т.е. на 180^о градусов. Следуя этому правилу можно сразу записать тригонометрическую форму числа , зная тригонометрическую форму числа .

По формуле Муавра при имеем:

.

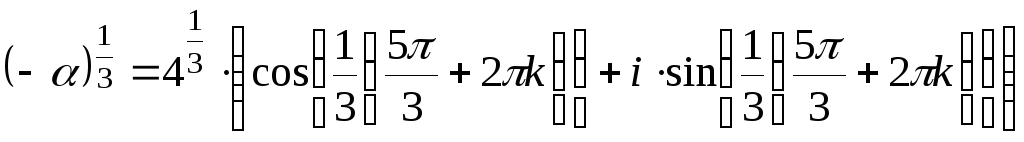Отсюда, .

Уравнение третьей степени имеет ровно три корня, которые можно найти, взяв . Итак, искомые корни заданного уравнения имеют вид:

при

при

при

г) Если комплексное число задано в алгебраической форме , то в комплексной плоскости ему соответствует точка с координатами . Если комплексное число задано в тригонометрической форме , то ему соответствует точка конца вектора, который начинается в начале координат, имеет длину равную и образует угол с положительным направлением оси .

Имеем

, ,

, ,

, ,

, ,

, ,

Задача №2. Указать на комплексной плоскости все точки , для которых выполняется неравенство. Сделать чертеж.

, где – комплексное число.

Решение.

Представим комплексное число в алгебраической форме , тогда заданное неравенство примет вид:

или

Введем в рассмотрение новое комплексное число , где , , тогда заданное неравенство можно записать в виде . Модуль комплексного числа равен , следовательно, заданное неравенство принимает вид:

или

Рассмотрим первое неравенство . Так как равенство является уравнением окружности с центром в точке и радиусом , то рассматриваемому неравенству удовлетворяют все точки комплексной плоскости, лежащие от точки на расстоянии большем, чем , т.е. все точки, лежащие с внешней стороны окружности .

Рассмотрим второе неравенство . Так как равенство является уравнением окружности с центром в точке и радиусом , то рассматриваемому неравенству удовлетворяют все точки комплексной плоскости, лежащие от точки на расстоянии меньшем или равном , т.е. все точки, лежащие с внутренней стороны окружности и на окружности .

Таким образом, геометрическим местом точек, координаты которых удовлетворяют одновременно двум неравенствам, является кольцо, ограниченное сверху окружностью , а снизу – окружностью . При этом точки верхней окружности также являются решением заданного двойного неравенства, а точки нижней окружности – не являются.

Сделаем чертеж.

Задача №3. Найти сумму, разность, произведение и частное чисел и в алгебраической форме. Найти тригонометрическую форму этих чисел. Найти их произведение и частное в тригонометрической форме.

,

Решение.

Сложение, вычитание и умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.

Найдем сумму чисел и :

Найдем разность чисел и :

Найдем произведение чисел и :

Найдем частное чисел и (см. задание 1 пункт а)):

Найдем тригонометрическую форму числа (см. задание 1 пункт б)):

, ,

, , , .

Итак, модуль числа равен , главная часть аргумента числа равна , тригонометрическая форма числа имеет вид:

Найдем тригонометрическую форму числа (см. задание 1 пункт б)):

, ,

, , , .

Итак, модуль числа равен , главная часть аргумента числа равна , тригонометрическая форма числа имеет вид:

Найдем произведение чисел и в тригонометрической форме. При умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются. Следовательно,

,

Проверка.

, что совпадает с результатом, найденным в алгебраической форме.

Найдем частное чисел и в тригонометрической форме. При делении двух комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются. Следовательно,

,

Проверка.

, что совпадает с результатом, найденным в алгебраической форме.

Задачи для расчетно-графической работы

по теме «Комплексные числа»

Задача №1. Даны в алгебраической форме два числа a и b:

а) Найти алгебраическую форму числа = a/b;

б) Найти тригонометрическую форму числа ;

в) Решить уравнение z³+=0

г) Изобразить числа , - и полученные корни уравнения z³+=0 точками на комплексной плоскости.

1	a = b =	2	a = b =
3	a = b =	4	a = b =
5	a = b =	6	a = b =
7	a = b =	8	a = b =
9	a = b =	10	a = b =
11	a = b =	12	a = b =
13	a = b =	14	a = b =
15	a = b =	16	a = b =
17	a = b =	18	a = b =
19	a = b =	20	a = b =
21	a = b =	22	a = b =
23	a = b =	24	a = b =
25	a = b =	26	a = b =
27	a = b =	28	a = b =