Пример 7.

Проверим выполняются ли свойства у бинарного отношения  заданного на множестве , если известно, что xy тогда и только тогда, когда .

Таким образом, .

1. Рефлексивность: для любого x X выполняется xx

для любого x X выполняется , значит рефлексивность выполняется.

2. Симметричность: для любых x, y  X из xy следует y x

для любых x, y  X из следует , так как умножение чисел коммутативно, значит симметричность выполняется.

3. Транзитивность: для любых x, y, z  X из xy и yz следует xz

так как x, y, z  X и выполняются неравенства и , значит x, y, z – это числа либо одновременно отрицательные, а произведение отрицательных чисел всегда больше нуля, либо одновременно неотрицательные, тогда выполняется неравенство , значит свойство транзитивности выполняется.

4. Так как выполняются свойства рефлексивности, симметричности и транзитивности, то бинарное отношение  обладает свойством эквивалентности.

Класс эквивалентности порожденный -4, состоит из чисел -4, -3, -2: ,, , т.е .

Ясно, что этот же класс порождается -3 и -2: .

Класс эквивалентности порожденный 1, состоит из 1, 2, 3: , , , т.е. .

Ясно, что этот же класс порождается 2 и 3: .

Таким образом, это бинарное отношение  «быть одного знака». Множество X можно разбить на два класса – отрицательные и положительные числа.

5. Антисимметричность: для любых x, y  X из xy и yx следует x=y.

существуют такие х и у, что если и ,то при этом , например, и , но при этом , значит свойство антисимметричности не выполняется.

6. Так как выполняются свойства рефлексивности и транзитивности, но не выполняется свойство антисимметричности, то бинарное отношение  не обладает свойством частичного порядка.

Упражнения для выполнения

1. Составьте все упорядоченные пары из элементов множества .

2. Напишите такие упорядоченные пары элементов множества , в которых первый элемент больше второго.

3. Изобразите при помощи графа пары .

4. Дан граф для бинарного отношения (см. Рисунок 2), заданного на множестве , , если х делится на y:

Рисунок 2. Пример графа

Проверьте, все ли упорядоченные пары отмечены на графе для бинарного отношения .

5. Равны ли следующие упорядоченные пары:

   1. <a, {a, b, c}, b, c > и <a, {a, b, c}, {b, c} >;

   2. <a, {a, b, c}, b, c > и <a, {a, b, c}, b, c>;

   3. <a, {a, b, c}, b, c > и <a, {a, b, c}, с, b>;

   4. <a, {a, b, c}, b, c > и <a, {a, b, c}, a, b, c>.

6. Пусть , . Выпишите все элементы декартова произведения множеств:

   1. ;

   2. ;

   3. ;

   4. .

7. Из цифр 1, 2, 3, 4, 5 составьте все двухзначные числа. Как связано получившееся множество с декартовым произведением , где ?

8. Известно, что

.

Найдите множества Х и А.

9. Дано множество .

   1. запишите все элементы декартового произведения множества ;

   2. изобразите с помощью графа те упорядоченные пары множества , в которых:

• первый элемент больше второго;

• первый элемент меньше второго;

• первый элемент меньше или равен второму;

• первый элемент равен второму.

10. Запишите в виде прямоугольных таблиц все элементы декартового произведения , где

    1. ,;

    2. , ;

    3. , .

Какой можно сделать вывод о количестве элементов декартового произведения ?

11. Сколько элементов в декартовом произведении , если:

    1. , ;

    2. , ;

    3. , .

12. Изобразите графически на плоскости бинарное отношение на множестве .

    1. ;

    2. ;

    3. ;

    4. .

13. На Рисунок 3 изображены графы отношений и . Запишите эти отношения и и им обратные.

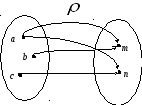
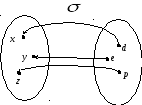
Рисунок 3. Графы отношений и

14. На множестве всех людей заданы отношения «быть сыном», «быть братом», «быть матерью», «быть другом». Назовите обратные им отношения.

15. Если , запишите бинарное отношение .

16. Даны множества и . На множестве заданы бинарные отношения и .

    1. , если ;

    2. , если а делится на b.

Запишите все упорядоченные пары, которые принадлежат бинарному отношению и .

17. Дано множество . Бинарное отношение задано следующим образом:

Рисунок 4. Пример изображения упорядоченных пар не координатной плоскости

Выяснить свойства отношения .

18. Пусть и , если .

Рисунок 5. Пример изображения упорядоченных пар не координатной плоскости

1. проверить все ли упорядоченные пары отмечены на координатной плоскости;

2. выяснить свойства отношения . Какой вывод можно сделать в случае выполнения свойства бинарного отношения.

1. Дано множество . На множестве задано бинарное отношение :

   1. изобразите упорядоченные пары с использованием графа;

   2. какие свойства выполняются у бинарного отношения ;

   3. как видно по графу выполнимость свойств бинарного отношения. Сформулируйте, как отображается каждое свойство бинарного отношения на графе.

2. Даны графы бинарных отношений:

   1. какие из отношений рефлексивны и почему?;

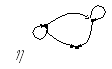
Рисунок 6. Примеры граф

2. какие из отношений симметричны и почему?;

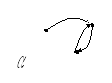
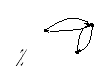
Рисунок 7. Примеры граф

3. какие из отношений транзитивны и почему?;

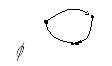
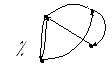
Рисунок 8. Примеры граф

4. какие из отношений антисимметричны и почему?;

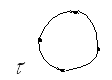
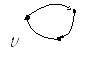
Рисунок 9. Примеры граф

21. Дано множество . На множестве заданы бинарные отношения и .

    1. , если ;

    2. , если .

Запишите все упорядоченные пары, которые принадлежат бинарным отношениям и . Выясните свойства бинарных отношений.

22. Пусть . На множестве задано бинарное отношение .

Выпишите все пары, принадлежащие бинарному отношению и выясните, каким свойствам удовлетворяет данное бинарное отношение.

23. Исследуйте на свойства бинарное отношение на множестве (в случае невыполнения свойства привести пример).

    1. М – множество натуральных чисел, , если х делится на у;

    2. М – множество прямых на плоскости, , если прямая а перпендикулярна прямой b;

    3. М – совокупность множеств, , если Ø.

24. Пусть Х – множество людей. На задано бинарное отношение : , если х является матерью у. Известно, что и . Верно ли утверждение: ?

25. Пусть Х – множество людей. На задано бинарное отношение : , если х и у знакомы. Будет ли транзитивно?

26. Пусть Х – множество студентов юридического факультета ЧИ БГУЭП. На задано бинарное отношение : , если х и у учатся на одном курсе. Выясните свойства бинарного отношения .

27. Исследовать бинарные отношения на множестве людей:

    1. «быть братом»;

    2. «любить»;

    3. «быть отцом»;

    4. «быть подчиненным»;

    5. «быть в одной команде».

28. Проверить обладает ли бинарное отношение на множестве бинарными свойствами:

    1. xy, если х делится на у;

    2. xy, если делится на 4;

    3. xy, если ;

    4. xy, если ;

    5. xy, если .

29. Дано множество . Доказать, что следующие отношения есть отношения эквивалентности, и построить соответствующее разбиение множества X:

    1. xy, если ;

    2. xy, если делится на 2.

30. Доказать, что следующие отношения есть отношения частичного порядка, и построить диаграммы частично упорядоченных множеств:

    1. отношение на множестве-степени множества ;

    2. отношение на множестве : xy, если y делится на x.

31. Являются ли следующие отношения функциями:

    1. ;

    2. ;

    3. .

32. Задано бинарное отношение = {<2, 2>, <2, 4>, <1, 4>, <4, 1>, <4, 2>}.Найдите область определения, область значения и ^-1.

33. Найдите композиции и и укажите область определения и область значения:

    1. , ;

    2. , ;

    3. , .

34. Заполните пустые ячейки в таблице:

Дано	Связь	Результат
<a, {a, b, c}, b, c >		<a, {a, b, c}, с, b>
бинарное отношение на множестве
бинарное отношение на некотором множестве
бинарное отношение на некотором множестве

1 При выполнении композиции вначале выполняется внутреннее бинарное отношение, после чего – внешнее.

13