ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Элементы комбинаторики
Процесс получения навыков подсчета комбинаторных объектов можно расчленить на три этапа в зависимости от времени обучения и методов подсчета:
подсчет методом непосредственного перебора;
подсчет с использованием комбинаторных принципов;
подсчет с использованием формул комбинаторики.
Справочный материал Перебор возможных вариантов в комбинаторных задачах
Рисунок 1. Виды комбинаторных задач
Пример.
В магазине продают шарфы трех цветов: зеленый, голубой и розовый. Подружки покупают себе по одному шарфу. Сколько существует различных вариантов покупок для этих девочек?
Решение.
Что дано? Шарфы трех цветов.
Что нужно сделать? Узнать количество способов покупки двух шарфов.
Поскольку в условии задачи не сказано о том, что подружки покупают шарфы различных цветов, то они могут купить либо два шарфа одного цвета, либо два шарфа различных цветов.
Могут быть куплены следующие шарфы:
зеленый, зеленый
зеленый, голубой
зеленый, розовый
голубой, голубой
розовый, розовый
розовый, голубой
Ответ. Возможно 6 способов покупки двух шарфов.
Перебор объектов с помощью графов в комбинаторных задачах
Пример.
Сколько различных трехзначных чисел можно записать с помощью цифр 1, 2, 3 при условии, что цифры в числе могут повторяться?
Решение.
Что дано? Цифры 1, 2, 3.
Что нужно сделать? Узнать количество способов составления трехзначных чисел.
Перебор вариантов можно организовать следующим образом. Выписать все числа, начинающиеся с цифры 1 в порядке их возрастания; затем – начинающиеся с цифры 2; после чего – начинающиеся с цифры 3 (см. Рисунок 2). Таких комбинаций получим 27. При переборе легко было упустить какую–нибудь из них.
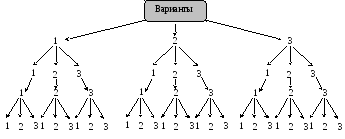
Рисунок 2. Перебор объектов при помощи графа–дерева
Ответ. Возможно 27 способов записи трехзначных чисел.
П
ример.
При встрече каждый из друзей пожал другому руку. Сколько рукопожатий было сделано, если друзей было четверо?
Решение.
Что дано? 4 друга.
Что нужно сделать? Узнать количество способов рукопожатия рук другу.
Четырех друзей поместим в вершины графа и проведем все возможные ребра, которые будут обозначать рукопожатия каждой пары друзей (см. Error: Reference source not found). Из рисунка видно, что граф имеет 6 ребер, значит, и рукопожатий было сделано 6.
Ответ. Возможно 6 способов рукопожатий.
Перебор объектов с помощью составления таблиц вариантов в комбинаторных задачах
Пример.
Сколько различных двухзначных чисел можно записать с помощью цифр 1, 2, 3 при условии, что цифры в числе могут повторяться?
Решение.
Что дано? Цифры 1, 2, 3.
Что нужно сделать? Узнать количество способов составления двухзначных чисел.
Составим таблицу всевозможных вариантов составления двухзначных чисел следующим образом:
Таблица 1. Таблица вариантов
-
вторая цифра
первая цифра
1
2
3
1
11
12
13
2
21
22
23
3
31
32
33
Из Таблица 1 видно, что можно образовать 9 различных двухзначных чисел.
Ответ. Возможно 9 способов составления двухзначных чисел.