Тема: «ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЁ ПРИЛОЖЕНИЯ»
План лекции
§ 1. Предел и непрерывность функций
§ 2. Производная функции, ее геометрический и физический смысл
1. Производная функции
2. Геометрический смысл производной
3. Уравнения касательной и нормали к кривой
4. Физический смысл производной
5. Экономический смысл производной.
§ 3. Сложная функция и ее производная
§ 4. Формулы дифференцирования
§ 5. Обратная функция и ее производная
§ 6. Неявная функция и ее производная
§ 7. Производные высших порядков
§ 8. Возрастание и убывание функции. Признаки возрастания и убывания функции
§ 9. Экстремумы функции. Необходимые условия существования экстремума
§
10. Достаточные условия существования
экстремума
Первое достаточное условие.
Второе достаточное условие
§ 11. Выпуклость графика функции. Достаточное условие выпуклости
§ 12. Точка перегиба. Необходимое и достаточное условия существования точки перегиба .
§ 13. Асимптоты кривой.
§ 14. Общая схема исследования функций и построения графиков
§ 15. Наибольшее и наименьшее значения функции на отрезке
Тема:
ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЁ ПРИЛОЖЕНИЯ
Производная функции и некоторые ее приложения известны по школьному курсу. Однако ввиду огромной важности производной при изучении различных разделов математики и других дисциплин, целесообразно повторить ряд вопросов, связанных с этим важным понятием.
§ 1. Предел и непрерывность функций
Напомним известные нам из курса математики средней школы определения понятий предела и непрерывности функций и приведем некоторые их обобщения и дополнения, нужные для дальнейшего.
Число
А называется
пределом функции
f(x)
в точке х=а, А
= lim
f(x)
(или f(xA
при xa),
если для любого
>0
существуеттакое
>0, что |х
— а|<
|f(x)—A|<B.
Н
апример,
В самом
деле, для данного
> 0, как видно из рис.
1,
если
в качестве
взять наименьшее из
чисел
и
,
то при| х — 2|
<
будем иметь
,
т. е. |
х2
— 4|<
.
В этом примере предел функции при х2 равен значению
функции в этой точке 4 = 22. Но это не всег» да так.
Рассмотрим на отрезке [—1; 1] функцию f(х)= [1—|x|],
где квадратные скобки означают, что при каждом х берется
целая часть числа, заключенногов скобках
(
например
)
Очевидно,
что при x
[—1;
1] и х
0
имеем
Рис. 1
следовательно, f(x) = [1—|x|]=0. При х = 0 получим f(0) = [1—|0|]=[1]= 1. График функции f(x) = [l —|х|] изображен на рис. 2.
Из
рис. 55
видно, что lim
f(x)
= lim
[1 — |
х |]
= 0.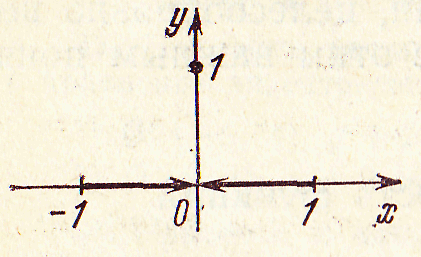 
Следовательно,
lim
f(х) = 0
f
(0) = 1.
Функция f(x) называется непрерывной в точке х=а
если предел функции при ха равен значению функции
в этой точке: lim f(x) = f(a).
Другими словами, функция f(x) непрерывна в точке х = а, если
для
любого
>
0 существует такое
>0,
что
|х
—
|<
|f(x)-f(а)|<
. Рис.
2.
Из
рассмотренных выше
примеров следует,
что функция f(x)=
непрерывна в
точке х
= 2,
функция f(x) = [1—|х|] не
является непрерывной
(разрывна) в точке
х =
0.
Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Если
в определении
предела вместо неравенств
|х —
|<
,
т. е.
—
< х <
+
,
рассмотреть неравенства
а <
х <
а +
,
то получим понятие
правого предела.
В этом случае
пишут
A=
f(
+ 0)= lim
f(x).
Аналогично,
рассматривая неравенства
-
< х <
,вводим понятие левого
предела:
A
= f(
— 0)=
lim f(x).
Предел
(двусторонний) функции в точке
существует в том
и только
в том случае, когда левый и
правый пределы
в этой точке существуют
и совпадают:
.
Заметим также, что при а = 0 вместо х0 + 0 и х 0 — 0 пишут соответственно х + 0 и х -0. Если правый (левый) предел совпадает со значением функции, то функция называется непрерывной справа (слева) в рассматриваемой точке.
Точка разрыва функции называется точкой разрыва первого рода, если в ней функция имеет конечные левый и правый пределы. Все остальные точки разрыва называются точками разрыва второго рода.
Число
А называется
пределом функции f(x)
при х
+,
f
(x)
= А,
если для любого
> 0 существует такое > 0, что
.
Например,
= 0. В самом деле, беря
,
при х>
имеем
.
Аналогично, число А называется пределом функции f(х) при х, lim f(x) = A, если для любого >0существует такое, А > 0, что
Функция
f(x)
называется бесконечно
большой при ха,
если для любого М
> 0 найдется
такое
>
0,что
При этом пишут
Записи
и
означают
соответственно, что
f(x)>
М и f(x)<-М
при |х—
а|<
.
Аналогично определяется бесконечно большая функция при xa + 0, ха-0, х+, х-, и употребляются соответствующие записи.
Напомним
еще, что
функция f(х) называется бесконечно
малой при х
а,если
Примерами
бесконечно малых функций служат функции
х2,
х3
при х
0,
sinх
при х
(в частности, при х
0),
cosх
при х
(k
— любое целое число).
Заметим, что если f(x)—бесконечно
малая (беек нечно большая) при х
а, то
—
бесконечно большая (бесконечно малая)
прих
а.
Говорят,
что функция f(x)
является при х
а
бесконечно малой более
высокого порядка, чем бесконечно
малая g(x)
при х
а,если
При этом очевидно, функция f(x) заведомо является бесконечно малой в обычном смысле. Действительно
Например,
функция f(x)
= x5
является бесконечно
малой более высокого порядка, чем
g(x)
= x3,
при х
0
