
Конспект_2часть
.pdf
рессией, будет много больше суммы SSyy€ относительно регрессии или, что то же самое, отношение
|
|
SS |
|
|
|
|
|
|
|
|
R2 |
= |
yy€ |
|
|
(3.21) |
|||||
SSyy |
|
|
SSyy |
|
||||||
|
|
|
|
|
|
|||||
не будет слишком отличаться от единицы. В этом случае отношение |
|
долж- |
||||||||
SSyy€ |
||||||||||
|
|
|
|
|
|
|
|
|||
но быть достаточно большим.
Всякая сумма квадратов связана с числом, называемым ее степенями свобо-
ды. Это число показывает, как много независимых элементов из n независимых чисел требуется для образования данной суммы квадратов. В частности, в сумму
SSyy входит (n-1) независимый элемент, т.к. при вычислении среднего значения y на n независимых величин была наложена одна связь. Величина
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 = |
SS |
|
|
|
|
|
||
|
|
yy |
|
, |
(3.22) |
|||||
S |
||||||||||
|
n −1 |
|||||||||
|
|
|
|
|
||||||
является общей дисперсией, вычисляемой по формуле (3.12).
Сумма квадратов SSyy€ относительно регрессии имеет (n-2) степени свободы,
так как n независимых значений функции отклика использовались для вычисления
двух коэффициентов уравнения регрессии. При большем количестве коэффици-
ентов число степеней свободы будет равно количеству наблюдений минус коли- чество оцениваемых параметров уравнения. Величина
|
|
|
SS |
yy€ |
|
€ |
2 |
( |
− |
|
− |
|
)2 |
|
|
|
|
|
|
|
|||||||
Sy2,ост = |
|
= |
å(yi − yi ) |
= å yi |
|
b0 |
|
b1xi |
(3.23) |
||||
n − 2 |
|
|
|||||||||||
|
|
|
|
n − 2 |
|
|
n − 2 |
|
|
||||
называется остаточной дисперсией. Для практических расчетов формула (3.23)
обычно приводится к виду:
|
|
|
å y 2 |
− b |
åy |
i |
− b |
å x |
y |
i |
|
|
Sy2,ост = |
i |
0 |
|
1 |
i |
|
. |
(3.23а) |
||||
|
|
n − 2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
В том случае, если выбранная математическая модель (вид уравнения рег- рессии) правильно описывает процесс, то остатки ei содержат только случайные
отклонения, вызванные погрешностью эксперимента. При неадекватности мате-
матического описания к случайным отклонениям добавляется систематическая погрешность, связанная с отклонением расчетных значений функции от реального процесса. За счет этого остаточная дисперсия окажется больше дисперсии, обу-
словленной только случайными погрешностями опытов.
77

Для оценки погрешности опытов чаще всего поступают следующим образом. В
одной точке при некотором х0 проводят m независимых параллельных опытов, ре-
зультаты которых не используются для определения коэффициентов уравнения
регрессии. Поскольку условия проведения опытов должны сохраняться неизмен- ными, то наблюдаемый разброс данных будет обусловлен только случайными по- грешностями. По этим данным рассчитываются среднее значение функции откли-
ка
|
|
|
|
|
|
1 |
m |
|
|
|
|
|
|
|
|
||
|
|
y0 = |
|
å y0,i |
|
|
|
|
|
|
|
(3.24) |
|||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
m i =1 |
|
|
|
|
|
|
|
|
|||
и дисперсия воспроизводимости |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
åm (y0,i − |
|
0 )2 |
|
å y |
0,2 i |
− |
1 |
(å y0,i )2 |
|
|
|||
|
|
|
y |
|
|
||||||||||||
|
|
|
|
m |
|
|
|||||||||||
Sвос2 = |
i =1 |
|
|
|
|
= |
|
. |
(3.25) |
||||||||
|
m −1 |
|
|
m −1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Затем проверяется, значимо ли отличается остаточная дисперсия от диспер-
сии воспроизводимости. Для этого при Sy2,ост > Sвос2 рассчитывается критерий
Фишера в виде
S 2
F = y,ост , (3.26)
Sвос2
который сравнивается с найденным по таблице распределения Фишера критиче- ским значением Fкр для выбранного уровня значимости α и чисел степеней свобо-
ды ν1 = n − 2 и ν 2 = m −1.
При F < Fкр принимается, что наблюдаемые отклонения результатов экспе-
римента от линии регрессии можно объяснить только влиянием случайных воз-
мущений, поэтому найденное уравнение регрессии признается адекватным ре- альному процессу. При F > Fкр более вероятно, что остаточная дисперсия вклю-
чает в себя наравне со случайными отклонениями систематическую погрешность,
обусловленную несоответствием математического описания реальному процессу. В этом случае гипотеза о предполагаемой линейной связи функции отклика с фак- тором отвергается, и уравнение регрессии признается неадекватным.
Если остаточная дисперсия будет меньше дисперсии воспроизводимости,
Sy2,ост < Sвос2 , то следует проверить, значимо ли они отличаются друг от друга.
Для этого вычисляется критерий Фишера в виде
78

F = |
|
|
|
вос2 |
|
|
|
S |
. |
(3.27) |
|||||
|
|
y2,ост |
|||||
|
|
S |
|
|
|||
Полученное значение сравнивают с табличным Fкр (α,ν1 = m −1,ν 2 − n − 2). При
F < Fкр принимается, что остаточная дисперсия и дисперсия воспроизводимости
статистически неразличимы, поэтому погрешность прогнозирования поведения функции отклика по уравнению регрессии находится в пределах погрешности опы-
тов. В этом случае уравнение регрессии признается адекватным.
При F > Fкр , то есть когда дисперсия воспроизводимости Sвос2 существенно
больше остаточной дисперсии Sy2,ост , оказывается, что погрешность эксперимен-
тальных данных существенно выше, чем погрешность расчета по уравнению рег- рессии, полученном на основе этих данных. Такая ситуация формально невоз- можна, т.к. величины остатков, из которых образуется остаточная дисперсия, включают в себя как случайные ошибки, входящие в дисперсию воспроизводимо- сти, так и дополнительную систематическую погрешность, связанную с возможной
неадекватностью модели. Поэтому необходимо проверить точность вычислений
дисперсий и условия проведения дублирующих опытов.
При отсутствии параллельных опытов невозможно оценить дисперсию вос-
производимости. Поэтому качество уравнения регрессии можно оценить, сопоста-
вив общую дисперсию относительно среднего Sy2 , рассчитанную по (3.12), с оста-
точной дисперсией. П этом случае критерий Фишера принимает вид:
|
|
|
|
|
y2 |
|
|
F = |
S |
(3.28) |
|||||
|
, |
||||||
|
|||||||
|
|
S |
y2,ост |
|
|||
Полученное значение сравнивают с критическим Fкр, взятым из таблицы рас-
пределения Фишера по числу степеней свободы ν1=n-1, ν2=n-2 и уровню значимо-
сти α. При F > Fкр принимается, что уравнение регрессии соответствует результа-
там экспериментов, в противном случае уравнение регрессии признается неадек-
ватным.
При неадекватности уравнения регрессии следует перейти к другой математи-
ческой модели процесса, что может потребовать проведения дополнительных
экспериментальных исследований.
79
Лекция 17. ИССЛЕДОВАНИЕ КОЭФФИЦИЕНТОВ И УРАВНЕНИЯ РЕГРЕССИИ
Вычисленные по (3.6) и (3.7) коэффициенты регрессии bi являются приближен-
ными оценками «истинных» коэффициентов βi, входящих в уравнение (3.2). Если уравнение регрессии адекватно, то остатки ei имеют нормальное распределение с математическим ожиданием M(ei ) = 0 и дисперсией σ 2 = Sy2,ост . В этом случае
параметры ti, характеризующие разброс значений коэффициентов регрессии bi
относительно βI и рассчитываемые по формуле
ti |
= |
bi |
− βi |
, |
(3.30) |
||
|
|
|
|||||
Sbi |
|||||||
|
|
|
|||||
имеют распределение Стьюдента.
Среднеквадратичные отклонения параметров b0 и b1 определяются выраже-
ниями
|
|
|
|
|
|
|
|
S |
y,ост |
|
|
|
|
|
|
||||||
|
|
|
= |
|
|
|
|
x |
, |
(3.31) |
|||||||||||
Sb0 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
||||||||||||
|
|
|
|
|
|
|
å x2 |
|
− |
(å xi )2 |
|
||||||||||
|
|
|
|
|
|
n |
|
||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
y,ост |
|
||||||||||
|
|
|
= |
|
|
|
|
S |
(3.32) |
||||||||||||
Sb |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
å x2 |
− |
1 |
|
(å xi )2 |
|
||||||||||||
|
|
|
|
|
|
n |
|
||||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|||||
Доверительные интервалы, внутри которых с заданным уровнем значимости α находятся истинные значения оцениваемых параметров, будут равны
~ |
|
|
|
|
|
|
|
|
|
= b0 ± Sb0 tкр , |
(3.33) |
||||||||
b0 |
|||||||||
~ |
|
|
|
|
|
|
|
|
|
= b1 |
± Sb t |
кр , |
(3.34) |
||||||
b1 |
|||||||||
|
|
1 |
|
|
|||||
где критерий Стьюдента tкр находится по таблицам распределения для уровня
значимости α2 и числа степеней свободы ν = n − 2.
Для линии регрессии среднеквадратическое отклонение равно
|
|
|
|
|
|
1 |
|
|
(x − |
|
|
)2 |
|
|
|
||
|
|
y€ = |
|
y,ост |
+ |
|
x |
, |
(3.35) |
||||||||
S |
S |
||||||||||||||||
|
n |
å x2 − |
1 |
(å xi )2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
n |
|
|
|
||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|||
откуда доверительные интервалы линии регрессии составят
~ |
|
|
|
|
|
1 |
|
(x − |
|
|
)2 |
|
|
|
|||
|
|
|
|
|
|
x |
|
||||||||||
= b0 |
+ b1x ± Sy,остtкр |
+ |
. |
(3.36) |
|||||||||||||
y |
|
|
|
|
|
||||||||||||
n |
å x2 |
− |
1 |
(å xi )2 |
|||||||||||||
|
|
|
|
|
|
|
n |
|
|||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|||
80
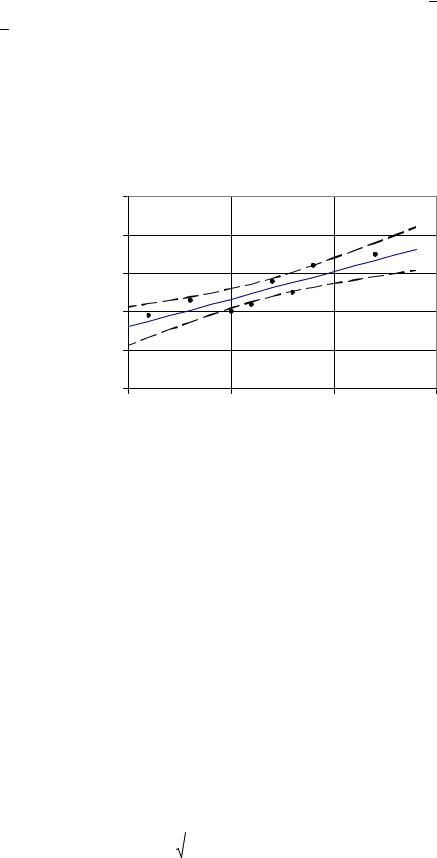
Наиболее узкий доверительный интервал будет при x = x , по мере удаления х от x в любом направлении доверительный интервал возрастает и точность пред- сказания значений функции отклика снижается.
На графике, как показано на рис.3.2, экспериментальные значения xi, yi нано-
сятся токами, зависимость y = f (x) - сплошной линией, а границы доверительных
интервалов - пунктирными линиями.
у |
|
|
|
9 |
|
|
|
8 |
|
|
|
7 |
|
|
|
6 |
|
|
|
5 |
|
|
|
4 |
|
|
х |
|
|
|
|
1 |
1,5 |
2 |
2,5 |
Рис.3.2. Пример построения графика зависимости y=b0+b1x
Тот факт, что некоторые экспериментальные значения могут находиться за доверительными границами, не противоречит теории, поскольку границы рассчи- тываются для математического ожидания (среднего значения) величины y, а не для индивидуальных значений yi.
При поиске коэффициентов уравнения регрессии y€= b0 + b1x неявно предпо-
лагалось, что значения х являются неслучайными величинами, не имеющими ве- роятностного распределения, в то время как функция отклика y обычно представ- ляется случайной величиной, имеющей распределение вероятностей со средним
β0 + β1x и остаточной дисперсией, оцениваемой выражением (3.23).
Теперь предположим, что X и Y образуют систему случайных величин с совме- стным распределением вероятностей f(X,Y). В этом случае коэффициент корре-
ляции
|
|
|
å(xi |
− |
|
)(yi |
− |
|
) |
|
|
|
||
rxy |
= |
|
x |
y |
|
(3.37) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
å(xi − |
|
)2 å(yi − |
|
)2 |
||||||||||
|
|
|
x |
y |
|
|
||||||||
будет определять меру линейной зависимости случайных величин X и Y. Для вы- числения более удобно представить выражение (3.37) в виде:
81
|
nå xi yi - å xi å yi |
|
rxy = |
[nå xi2 - (å xi )2 ] [nå yi2 - (å yi )2 ] . |
(3.37а) |
Значения коэффициента корреляции находятся в пределах -1£ rxy £ +1. Знак
коэффициента корреляции определяет направление изменения одной величины
при изменении другой. При rxy>0 увеличение значения x приводит в среднем к увеличению y, при rxy<0 - к уменьшению y. Абсолютная величина rxy определяет
тесноту линейной связи между x и y; при ½rxy½=1 все значения y будут находиться на прямой, описываемой уравнением (3.4). При rxy=0 величины x и y линейно не- зависимы.
Коэффициент корреляции связан с угловым коэффициентом b1, значение ко- торого равно тангенсу угла наклона линии регрессии к оси 0X. Из (3.7) и (3.37а)
можно получить:
b1 = |
nå yi2 - (å yi )2 |
rxy . |
(3.38) |
nå xi2 - (å xi )2 |
Таким образом, b1 и rxy весьма близки, но интерпретируются по разному. Ко-
эффициент корреляции измеряет линейную связь между x и y, в то время как b1
определяет угол наклона линии регрессии.
Поскольку значения величин x и y могут быть отягощены случайными погреш- ностями, то и параметры уравнения регрессии b0 и b1, коэффициент регрессии rxy и значения yi , рассчитываемые по найденному уравнению регрессии, также представляют собой случайные величины.
Для того, чтобы коэффициент корреляции rxy значимо отличался от нуля, не-
обходимо выполнение условия
tr = |
|
rxy |
|
n - 2 |
> tкр . |
(3.39) |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
1- rxy2 |
|||||||||
|
|
|
|
||||||
Параметр tкр определяется из таблицы t- распределения Стьюдента по числу степеней свободы n=n-2 и выбранному уровню значимости α.
При интерпретации коэффициента корреляции необходимо соблюдать боль- шую осторожность. Корреляционную зависимость не следует путать с причинной
зависимостью. Две независимые величины всегда некоррелированы и для них rxy=0. Обратное утверждение не имеет места: две некоррелированные величины не обязательно независимы, зависимость между ними может быть нелинейной. С
82

другой стороны, сильная корреляция двух переменных не обязательно означает
причинную взаимосвязь между ними. Возможно, что имеется некоторая иная не учтенная в эксперименте независимая переменная, которая обуславливает зна-
чения первых двух таким образом, что между ними наблюдается зависимость, близкая к линейной.
Если формально рассматривать x и y как случайные величины, то в качестве независимой переменной можно принять величину y и построить уравнение рег-
рессии в виде
x = a0 + a1y .
Коэффициенты a0 и а1 рассчитываются по формулам
a0 |
= |
å xi å yi2 |
− å yi å xi yi |
, |
|
nå yi2 |
− (å yi )2 |
||||
|
|
|
(3.40)
(3.41)
a = |
nå xi yi − å xi å yi |
. |
(3.42) |
|
|||
1 |
nå yi2 − (å yi )2 |
|
|
|
|
||
В общем случае получаются два различных уравнения регрессии y = b0 + b1x
и x = a0 + a1y , которые отвечают двум различным математическим формулиров-
кам задачи: в первом случае минимизируется сумма квадратов отклонений, взя- тых параллельно оси y, во втором случае - оси x. Прямые линии, описываемые этими уравнениями, совпадают при rxy=±1 и пересекаются под прямым углом при rxy=0 в точке с координатами (x,y ). Выбор зависимости y=f(x) или x=f1(y) должен соответствовать физическому смыслу задачи. Если оба уравнения имеют физи- ческий смысл, то выбор вида уравнения становится произвольным. В этом случае
используется то уравнение, в котором независимой переменной является наибо-
лее точно определяемая величина.
83
Лекция 18. ВЫБОР СТРАТЕГИИ ЭКСПЕРИМЕНТА
Допустим, необходимо экспериментальным путем найти зависимость некото-
рой функции Y от фактора Х, причем в значениях фактора отсутствует случайная ошибка, в то время как значения функции содержат случайные отклонения.
При планировании экспериментов возникает ряд вопросов:
1) В каком диапазоне значений фактора следует проводить эксперименты? С одной стороны, диапазон должен быть достаточно широким, чтобы получить за-
метный отклик на изменение значений фактора. С другой стороны, диапазон дол- жен быть достаточно узким, чтобы стало возможным представить результаты
наипростейшей моделью. После того, как диапазон будет выбран, для фактора можно ввести кодированные переменные, значения которых определяются выра- жением:
zi |
= |
2xi − xмax − xмin |
. |
(3.43) |
|
||||
|
|
xмax − xмin |
|
|
При xi = xмin zi = −1, при xi = xмax zi = 1.
2) Какого рода зависимость y = f (x) следует ожидать в выбранном диапазоне:
линейную, квадратичную или иную? Предположим, что предполагается, что дос-
товерной окажется модель первого порядка, однако полной уверенности в этом нет.
3)Какая модель будет более правдоподобной, если ранее выбранная модель окажется неадекватной? Если в качестве основной гипотезы принята линейная
модель, то при ее неверности более вероятной кажется какая-нибудь зависимость
второго порядка. Ситуация, когда действительна модель третьего порядка, пред- ставляется менее вероятной.
4)Какова ошибка воспроизводимости опытов? Если предварительной инфор-
мации об этом нет, то желательно провести параллельные опыты и оценить эту величину.
5)Сколько опытов будет необходимо для получения требуемой информации?
Этот вопрос решается с учетом располагаемых материальных ресурсов, числен- ности персонала, количества и качества измерительной аппаратуры и важности
задачи.
6)Сколько уровней варьирования следует выбрать для фактора X? Сколько
повторных опытов следует проводить в каждой точке?
84

Для определенности допустим, что во всем диапазоне изменения кодирован-
ного фактора −1≤ z ≤ 1 наиболее правдоподобна линейная зависимость, но, в крайнем случае, может оказаться более правильной квадратичная модель, при
этом дисперсия воспроизводимости неизвестна и возможно проведение 14 опы- тов.
a) 14 точек
-1 |
+1 |
|
б) 7 точек |
-1 |
+1 |
 в) 5 точек
в) 5 точек
-1 |
+1 |
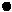 г) 4 точки
г) 4 точки
-1 |
+1 |
 д) 3 точки
д) 3 точки
-1 |
+1 |
 е) 3 точки
е) 3 точки
-1 |
+1 |
 ж) 3 точки
ж) 3 точки
-1 |
+1 |
Рис.3.3. Возможное расположение координат точек для
14 опытов
На рис.3.3. показаны
несколько возможных вариантов расположения
экспериментальных зна-
чений кодированного
фактора Z. Предполага- ется, что на всем диапа- зоне −1≤ Z ≤ +1 точки размещены равномерно,
Каждый из планов имеет по 14 степеней
свободы. Две из них идут
на оценки параметров b0
и b1. Оставшиеся 12 сте- пеней свободы распре-
деляются в зависимости от расположения точек и количества повторных опытов между остаточ- ной дисперсией и дис- персией воспроизводи- мости.
Относительная по-
грешность определения
значений коэффициен-
тов b0 и b1. пропорцио-
нальна их среднеквад-
ратичным отклонениям, определяемым по формулам (3.31) и (3.32). В знаменате-
ле этих выражений стоит величина 
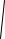 å xi2 − n1 (å xi )2 =
å xi2 − n1 (å xi )2 = 
 å xi2 − n x 2 . Для всех
å xi2 − n x 2 . Для всех
85

рассматриваемых вариантов (а) – (ж) среднее значение фактора z = 0 , поэтому в качестве оценки погрешности определения коэффициентов регрессии можно рас-
сматривать величину ε = |
1 |
, чем меньше ε, тем меньше ожидаемый разброс |
|
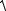 åzi2
åzi2
между «истинными» значениями параметров уравнения βi и определенными по результатам опытов bi.
В табл.3.2 приведены характеристики вариантов проведения опытов, пред- ставленных на рис.3.2.
Таблица 3.2
Основные характеристики стратегий эксперимента
№ |
|
|
(а) |
(б) |
(в) |
(г) |
(д) |
(е) |
(ж) |
|
|
|
|
|
|
|
|
|
|
1 |
Число степеней свободы ос- |
12 |
5 |
3 |
2 |
1 |
1 |
0 |
|
|
таточной дисперсии |
|
|
|
|
|
|
|
|
2 |
Число степеней свободы |
0 |
7 |
9 |
10 |
11 |
11 |
12 |
|
|
дисперсии |
воспроизводимо- |
|
|
|
|
|
|
|
|
сти |
|
|
|
|
|
|
|
|
3 |
Возможное |
количество па- |
14 |
7 |
5 |
4 |
3 |
3 |
2 |
|
раметров регрессии |
|
|
|
|
|
|
|
|
4 |
Оценка погрешности пара- |
0,431 |
0,401 |
0,333 |
0,309 |
0,316 |
0,289 |
0,267 |
|
|
метров регрессии ε |
|
|
|
|
|
|
|
|
Увеличение числа степеней свободы остаточной дисперсии повышает точ-
ность оценки адекватности уравнения регрессии, в то время как увеличение числа
степеней дисперсии воспроизводимости позволяет более точно оценить погреш- ность эксперимента. Количество уровней варьирования фактора определяет мак- симальное количество параметров регрессии, входящих в уравнение.
Вариант (а) не предполагает проведения дублирующих опытов, поэтому не по-
зволяет оценить погрешность эксперимента. С этой точки зрения от стратегии (а)
целесообразно отказаться.
Вварианте (ж) все опыты проводятся в двух точках на краях интервала. Любая двухпараметрическая кривая точно пройдет через две точки, не позволив оценить
адекватность математического описания. Такой вариант можно использовать
только при полной уверенности в справедливости выбранного вида уравнения регрессии. Если полной уверенности нет, то от этого варианта следует отказать-
ся.
Вварианте (б) опыты проводятся при варьировании фактора на 7 уровнях. Для линейной и квадратичной модели такое количество уровней излишне, при этом данная стратегия обладает достаточно высокой погрешностью оценки коэффици-
86
