
СЕМИНАР 6
.docСЕМИНАР 6
Вычисление определителей матриц, свойства определителей.
Вводная информация
Определитель матрицы.
Понятие определителя
матрицы, который обозначается через
![]() или
или
![]() ,
имеет смысл только для квадратных
матриц. Введем это понятие последовательно,
увеличивая размерность матриц.
,
имеет смысл только для квадратных
матриц. Введем это понятие последовательно,
увеличивая размерность матриц.
-
Определитель первого порядка. Рассмотрим матрицу, имеющую одну строку и один столбец
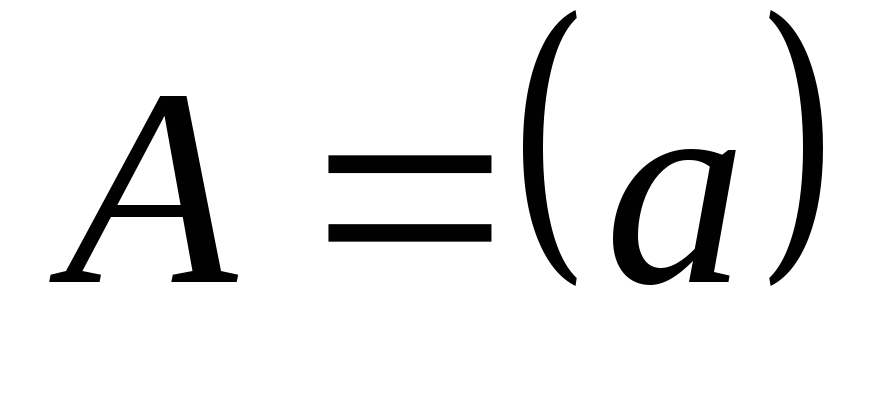 .
Тогда
.
Тогда
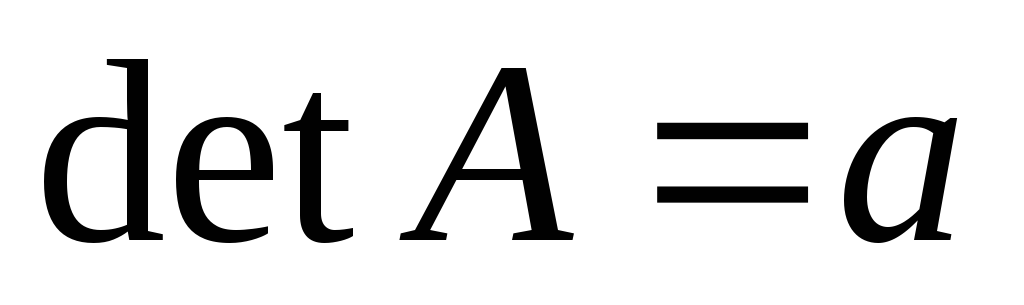 .
. -
Определитель второго порядка. Пусть
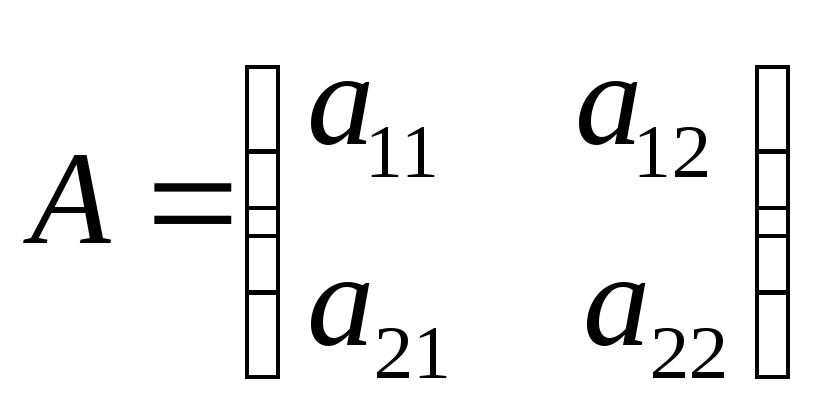 ,
тогда
,
тогда
 .
.
Пример.
![]() .
.
-
Определитель третьего порядка. Пусть
 ,
тогда
,
тогда
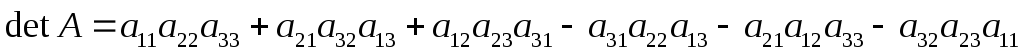 .
.
Пример.
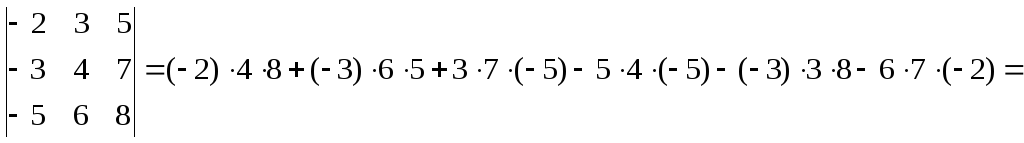
![]()
-
Определитель n-го порядка.
Определение.
Минором
элемента
![]()
![]() -матрицы
-матрицы
![]() называется определитель
называется определитель
![]() -го
порядка, соответствующий той матрице,
которая получается из матрицы
-го
порядка, соответствующий той матрице,
которая получается из матрицы
![]() после вычеркивания в ней
после вычеркивания в ней
![]() -ой
строки и
-ой
строки и
![]() -го
столбца. Минор элемента
-го
столбца. Минор элемента
![]() будем обозначать
будем обозначать
![]() .
.
Пример. Пусть
 ,
тогда
,
тогда
 .
.
Определение.
Алгебраическим
дополнением элемента
![]() называется
произведение
называется
произведение
![]() на минор
на минор
![]() и обозначается
и обозначается
![]() ,
т.е.
,
т.е.
![]() .
.
Пример. Пусть
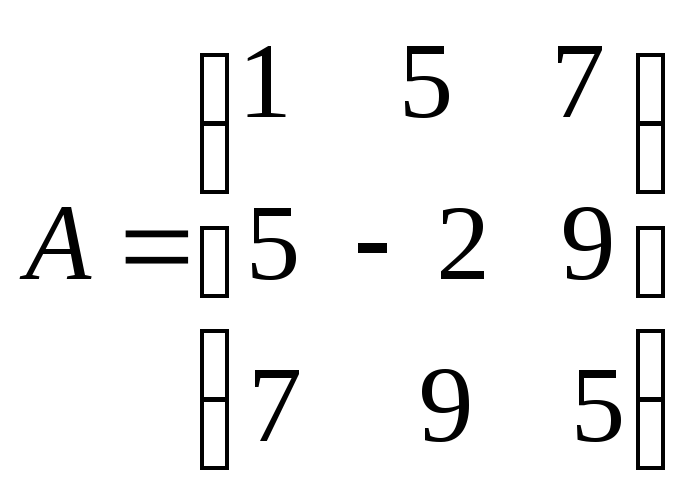 ,
тогда
,
тогда
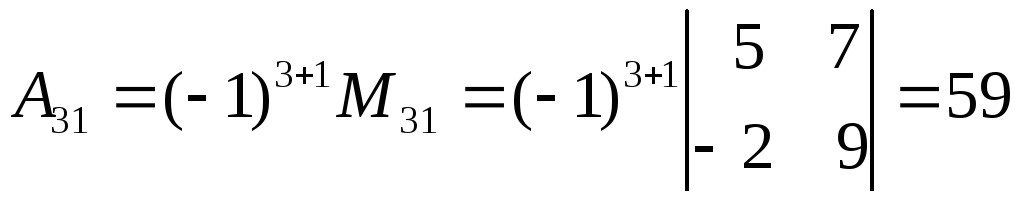 .
.
Определение.
Определителем
![]() -го
порядка (или определителем матрицы
-го
порядка (или определителем матрицы
![]() )
называется число
)
называется число
![]() ,
равное
,
равное
![]() .
Формула
.
Формула
![]() называется разложением определителя
по
называется разложением определителя
по
![]() -ой
строке.
-ой
строке.
Пример.
Разложим определитель
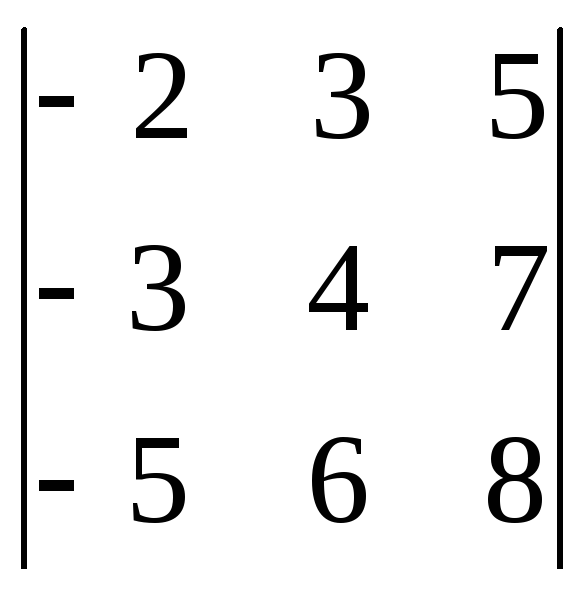 по второй
строке и вычислим его.
по второй
строке и вычислим его.
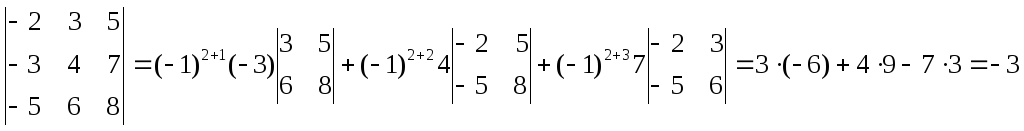 .
.
Формула разложения
определителя матрицы по
![]() -ому
столбцу имеет вид
-ому
столбцу имеет вид
![]() .
.
Пример. Разложим
определитель
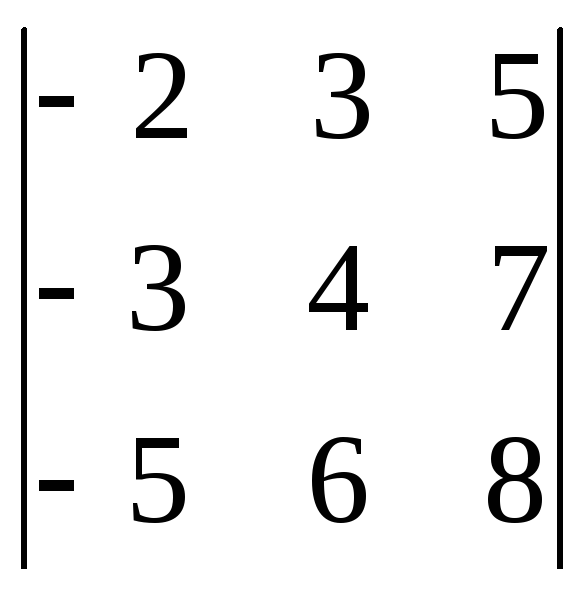 по третьему
столбцу и вычислим его.
по третьему
столбцу и вычислим его.
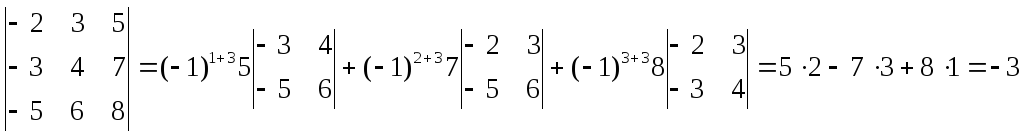 .
.
Свойства определителей.
Перечислим основные свойства определителей.
-
Определитель
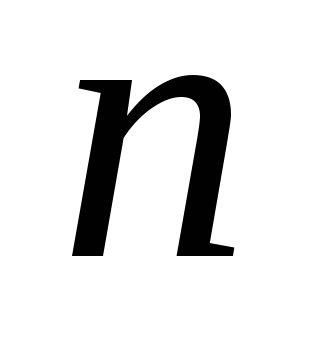 -го
порядка содержит
-го
порядка содержит
 слагаемых, каждое из которых представляет
собой произведение
слагаемых, каждое из которых представляет
собой произведение
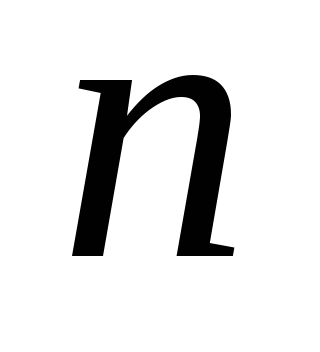 сомножителей, причем каждое произведение
содержит лишь по одному представителю
от каждой строки и каждого столбца.
сомножителей, причем каждое произведение
содержит лишь по одному представителю
от каждой строки и каждого столбца. -
 .
. -
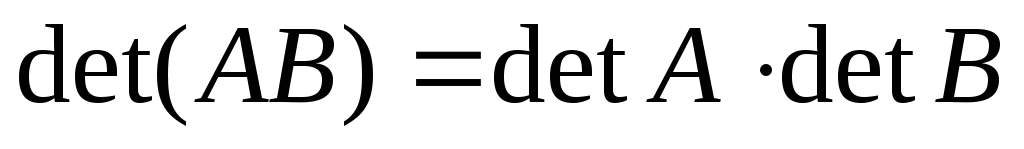 .
. -
При перестановке местами любых двух строк (столбцов) определитель меняет знак на противоположный.
-
Определитель с двумя равными строками (столбцами) равен нулю.
-
Общий множитель всех элементов любой строки (столбца) можно вынести за знак определителя.
-
Определитель матрицы, у которой все элементы, стоящие в какой-либо строке (столбце) равны сумме двух чисел, равен сумме двух определителей.
Пример.
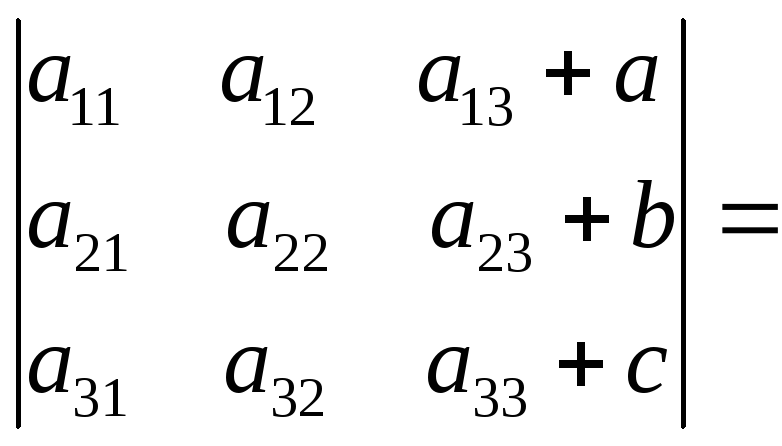
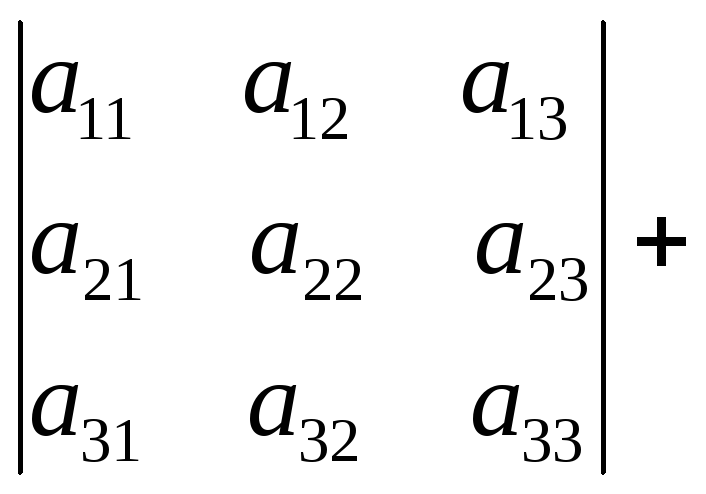
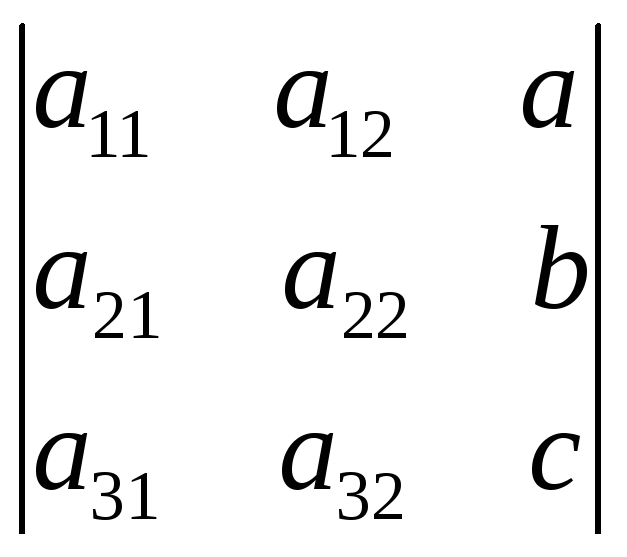 .
.
8. Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.
9. Если элементы двух строк (столбцов) определителя с учетом их порядка пропорциональны друг другу, то определитель равен нулю.
10. Если к элементам
некоторой строки (столбца) определителя
прибавить соответствующие элементы
другой строки (столбца), умноженные на
произвольное число
![]() ,
то величина определителя не изменится.
,
то величина определителя не изменится.
11. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.
Вычисление определителя методом разложения его по строке (столбцу) особенно эффективно, когда в этой строке (столбце) имеются нулевые элементы. Поэтому при вычислении определителей большой размерности целесообразно предварительно, используя перечисленные свойства определителей, сформировать такие строки (столбцы).
Пример.
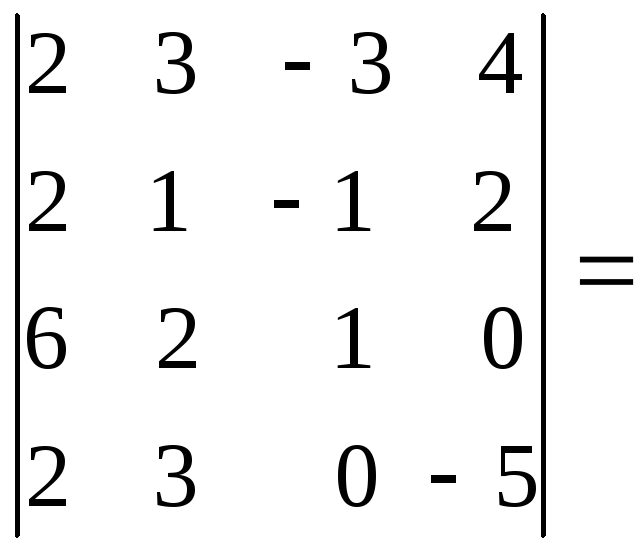 /прибавим
третий столбец ко второму столбцу/
/прибавим
третий столбец ко второму столбцу/
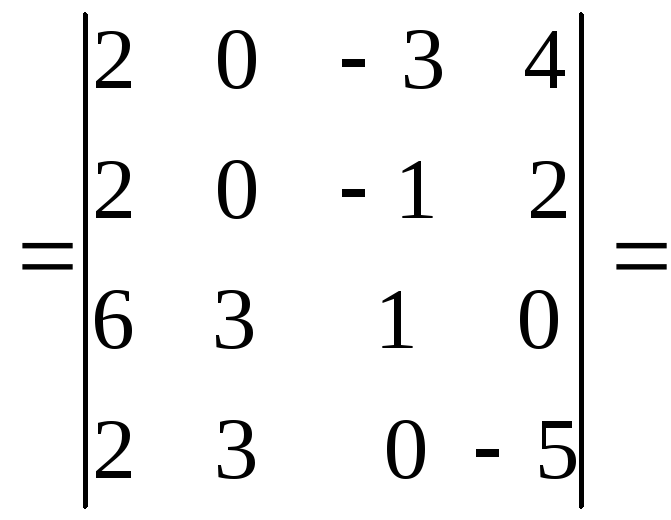 /вычтем
четвертую строку из третьей строки/
/вычтем
четвертую строку из третьей строки/
 /разложим
определитель по второму столбцу/
/разложим
определитель по второму столбцу/
 /вычтем вторую строку из первой строки/
/вычтем вторую строку из первой строки/
 /прибавим третий столбец ко второму
столбцу/
/прибавим третий столбец ко второму
столбцу/
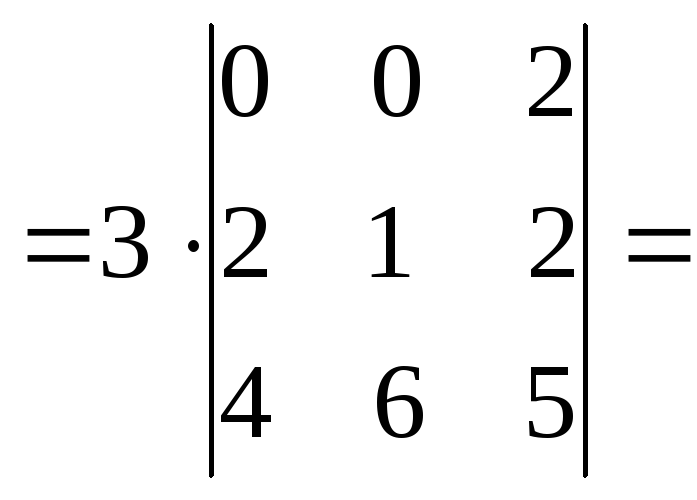 /разложим определитель по первой строке/
/разложим определитель по первой строке/
 / умножим первую строку на 2 и вычтем ее
из второй строки/
/ умножим первую строку на 2 и вычтем ее
из второй строки/
 /разложим
определитель по первому столбцу/
/разложим
определитель по первому столбцу/
![]() .
.
Метод Гаусса.
В численных методах при вычислении определителей применяют метод Гаусса, основанный на приведении определителя с помощью указанных выше преобразований к треугольному виду.
Пример.
Вычислим методом Гаусса тот же
определитель, что и в предыдущем примере.
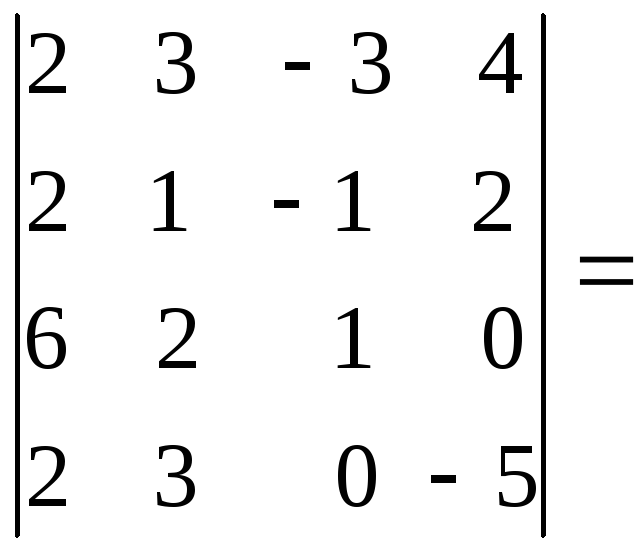 / вычитая
первую строку из второй, третьей и
четвертой, делаем нулевыми элементы в
них, стоящие в первом столбце (перед
вычитанием из третьей строки умножим
первую строку на 3)/
/ вычитая
первую строку из второй, третьей и
четвертой, делаем нулевыми элементы в
них, стоящие в первом столбце (перед
вычитанием из третьей строки умножим
первую строку на 3)/
 /поменяем
местами третью и четвертую строку/
/поменяем
местами третью и четвертую строку/
 /умножим
вторую строчку на
/умножим
вторую строчку на
![]() и вычтем ее
из четвертой строки/
и вычтем ее
из четвертой строки/
 / вычтем
третью строку из четвертой/
/ вычтем
третью строку из четвертой/
 /используя
свойства треугольной матрицы, вычисляем
определитель/
/используя
свойства треугольной матрицы, вычисляем
определитель/
![]() .
.
Метод рекуррентных соотношений.
Если матрица, определитель которой мы вычисляем, имеет достаточную симметрию, можно использовать метод рекуррентных соотношений.
Пример. Вычислим
методом рекуррентных соотношений
определитель
![]() -го
порядка
-го
порядка
 .
Разложим его по последнему столбцу.
.
Разложим его по последнему столбцу.
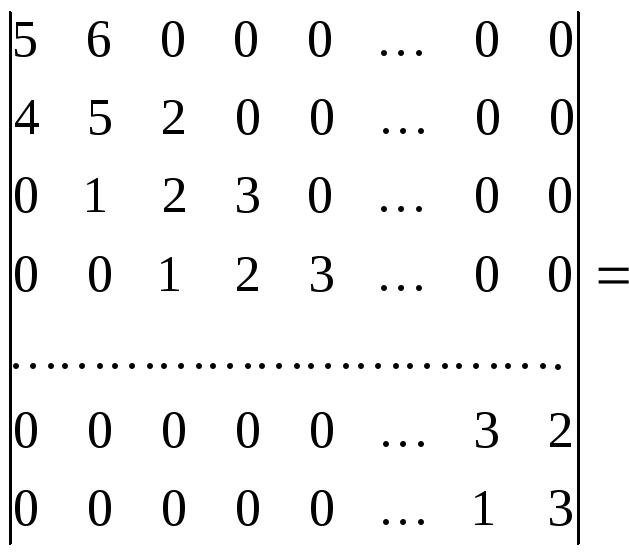

 /разложим
теперь определитель во втором слагаемом
по последней строке/
/разложим
теперь определитель во втором слагаемом
по последней строке/

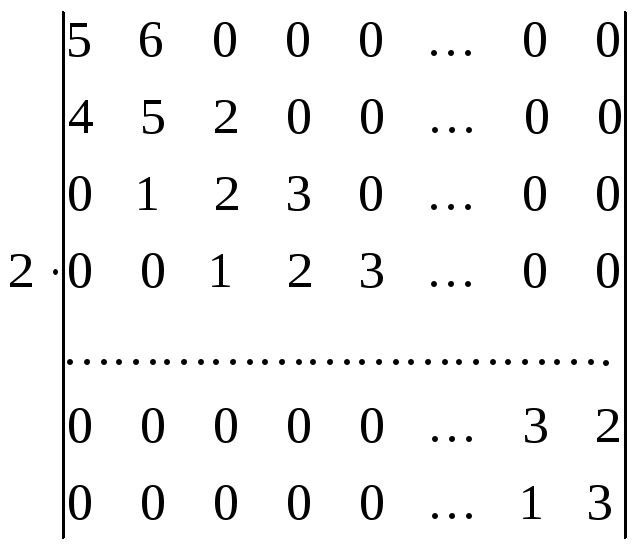 .
Замечаем, что мы теперь имеем три
определителя одинаковой структуры, но
разной размерности. Если мы обозначим
первоначальный определитель
.
Замечаем, что мы теперь имеем три
определителя одинаковой структуры, но
разной размерности. Если мы обозначим
первоначальный определитель
![]() -го
порядка через
-го
порядка через
![]() ,
то можно написать рекуррентное соотношение
,
то можно написать рекуррентное соотношение
![]() .
Чтобы воспользоваться этим соотношением,
вычислим несколько первых определителей:
.
Чтобы воспользоваться этим соотношением,
вычислим несколько первых определителей:
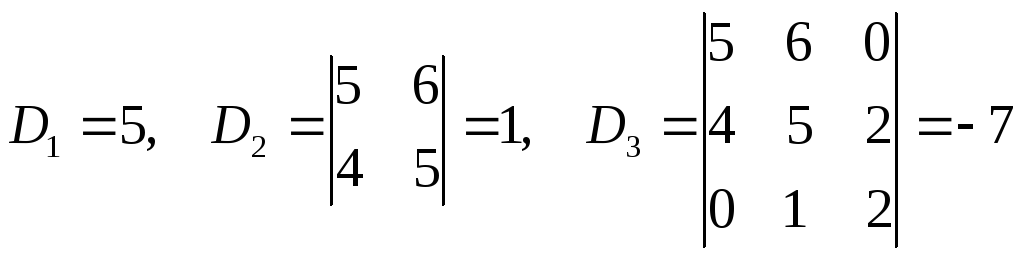 .
.
Далее, используя
рекуррентное соотношение, находим:
![]()
![]()
![]() .
Заметим, что
.
Заметим, что
![]()
![]()
![]()
![]()
![]() .
Следовательно, можно записать
.
Следовательно, можно записать
![]() и т. д. Вычисление первых определителей
дает общую формулу
и т. д. Вычисление первых определителей
дает общую формулу
![]() .
Чтобы завершить доказательство, проверим
справедливость этой формулы методом
математической индукции. Предполагая,
что эта формула верна для определителя
.
Чтобы завершить доказательство, проверим
справедливость этой формулы методом
математической индукции. Предполагая,
что эта формула верна для определителя
![]() -го
порядка, мы должны показать, что
определитель
-го
порядка, мы должны показать, что
определитель
![]() -го
порядка равен
-го
порядка равен
![]() .
Находим, используя рекуррентное
соотношение,
.
Находим, используя рекуррентное
соотношение,
![]() .
Полученное выражение доказывает
справедливость формулы
.
Полученное выражение доказывает
справедливость формулы
![]() .
.
ЗАДАЧИ
1. Задачи удовлетворительного уровня сложности.
Вычислить определитель второго порядка.
6.1.
![]() .
6.2.
.
6.2.
![]() .
6.3.
.
6.3.
![]() .
6.4.
.
6.4.
![]() .
6.5.
.
6.5.
![]() .
6.6.
.
6.6.
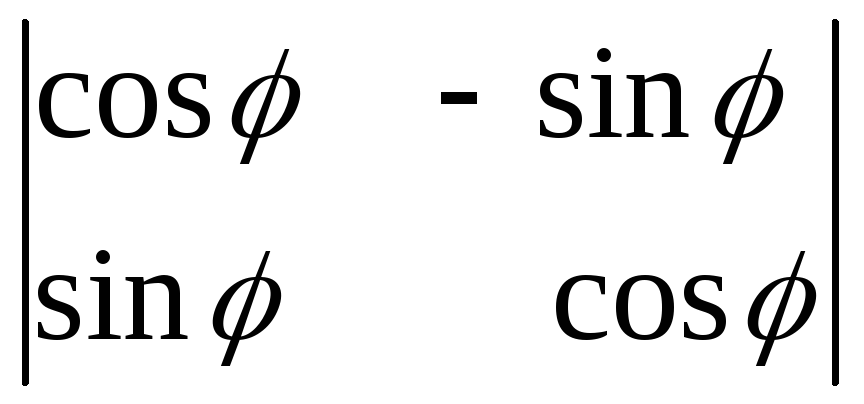 .
6.7.
.
6.7.
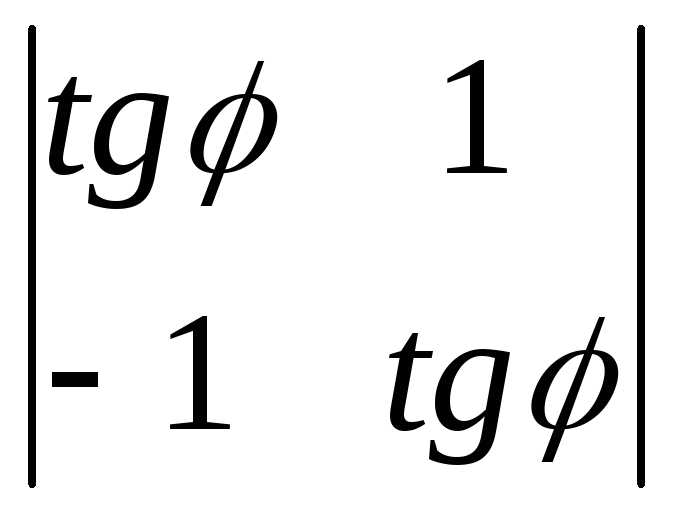 .
6.8.
.
6.8.
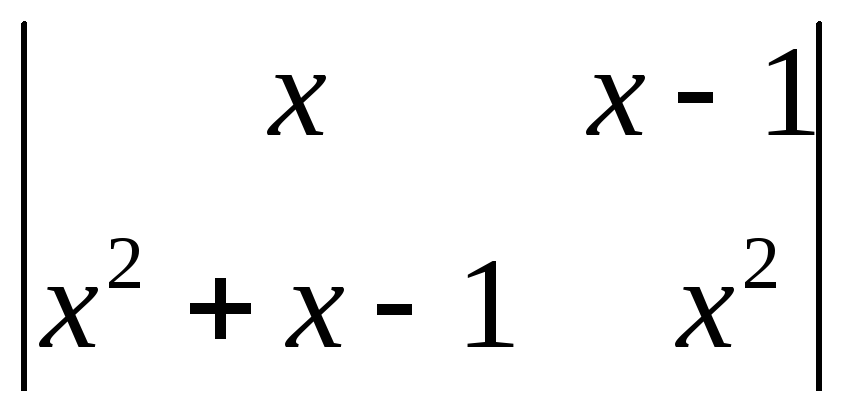 .
6.9.
.
6.9.
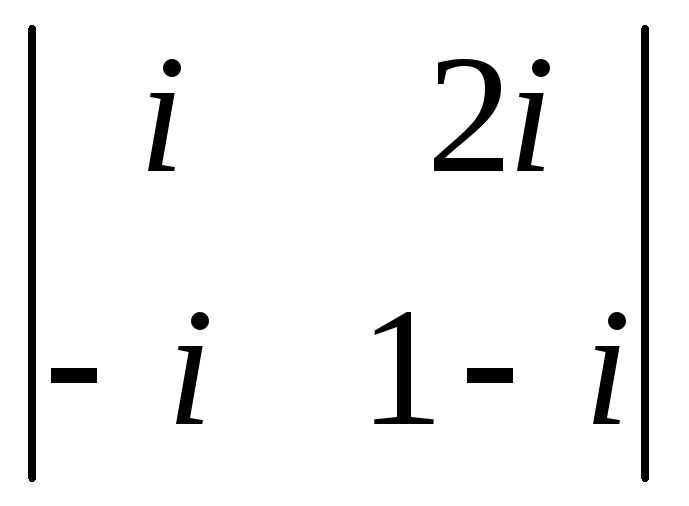 .
.
6.10.
 .
.
Решить уравнения.
6.11.
 .
6.12.
.
6.12.
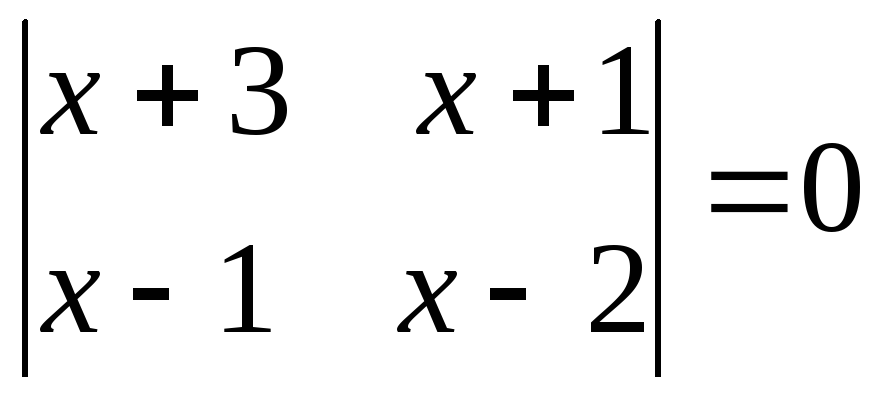 .
6.13.
.
6.13.
 .
.
6.14.
 .
6.15.
.
6.15.
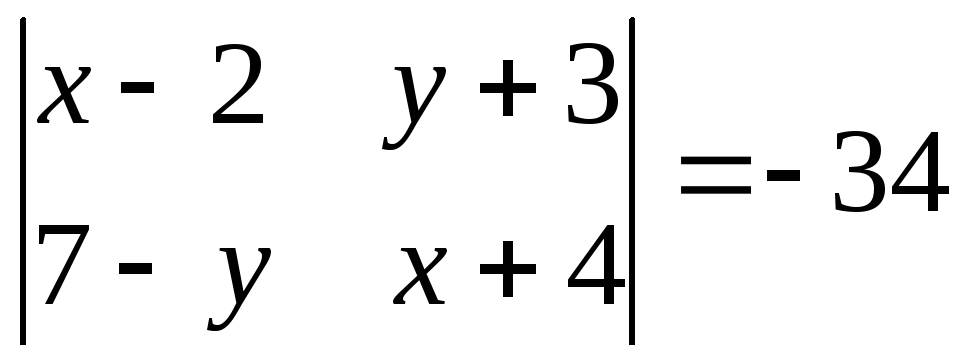 .
6.16.
.
6.16.
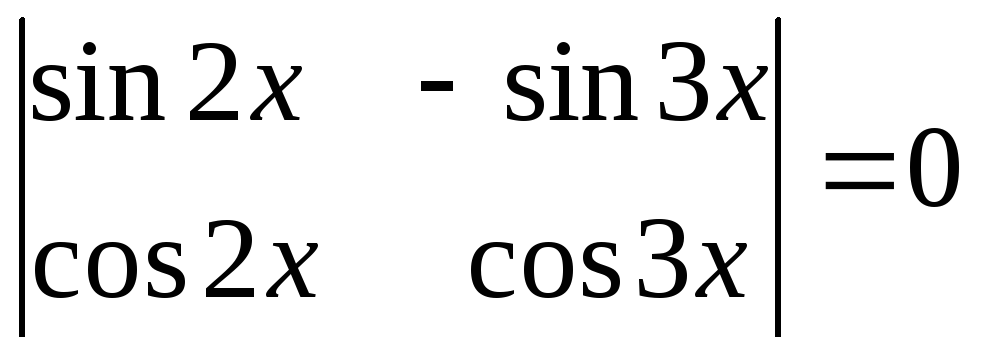 .
.
Вычислить определители.
6.17.
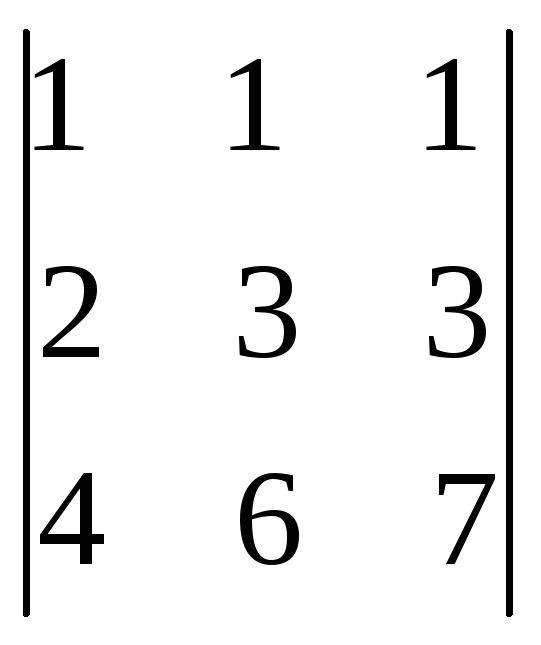 .
6.18.
.
6.18.
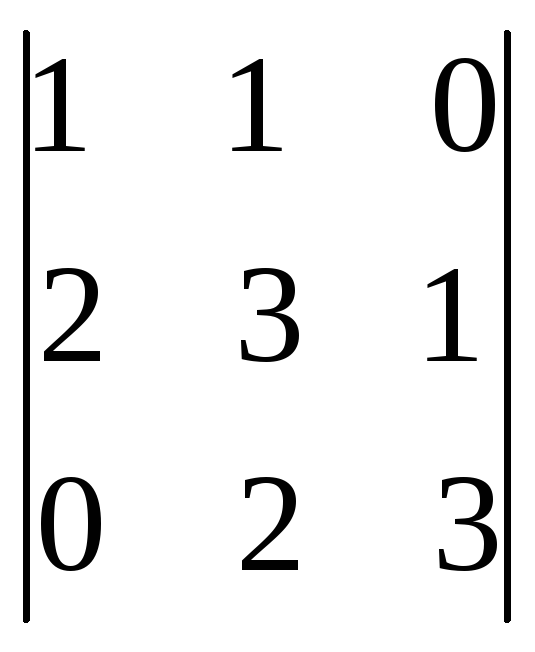 .
6.19.
.
6.19.
 .
6.20.
.
6.20.
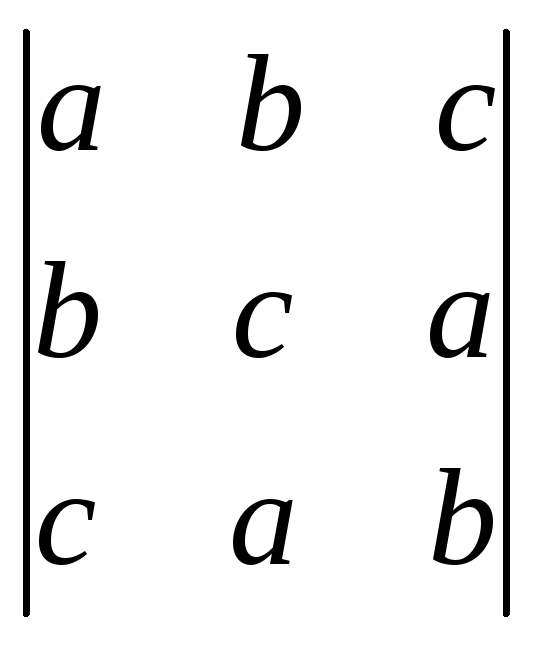 .
.
6.21.
 .
6.22.
.
6.22.
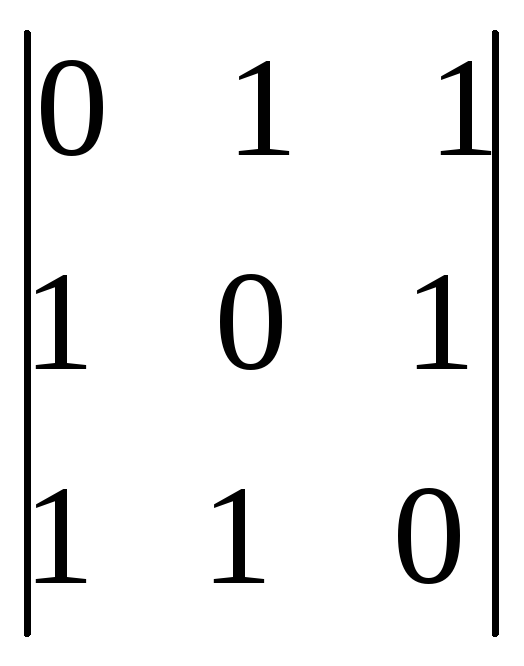 .
6.23.
.
6.23.
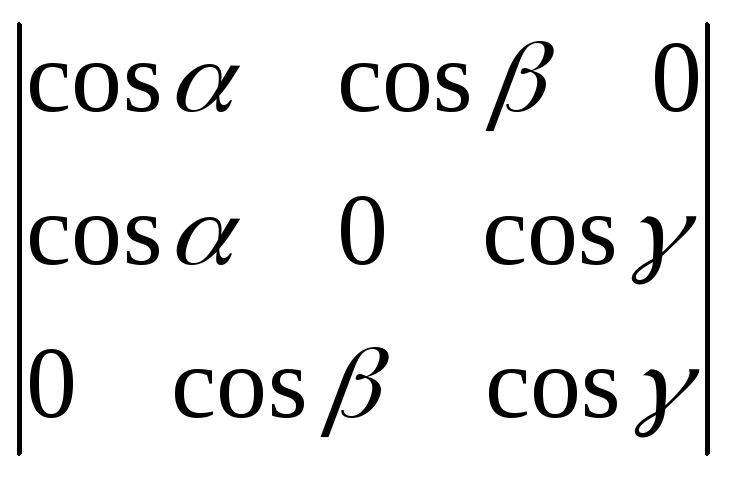 .
6.24.
.
6.24.
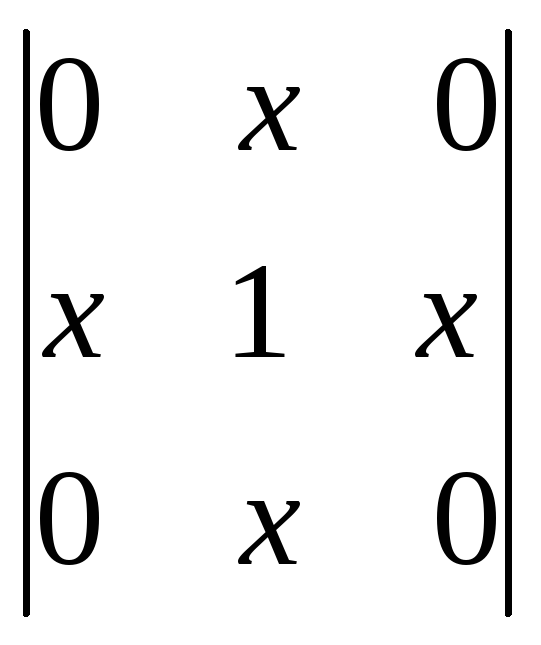 .
6.25.
.
6.25.
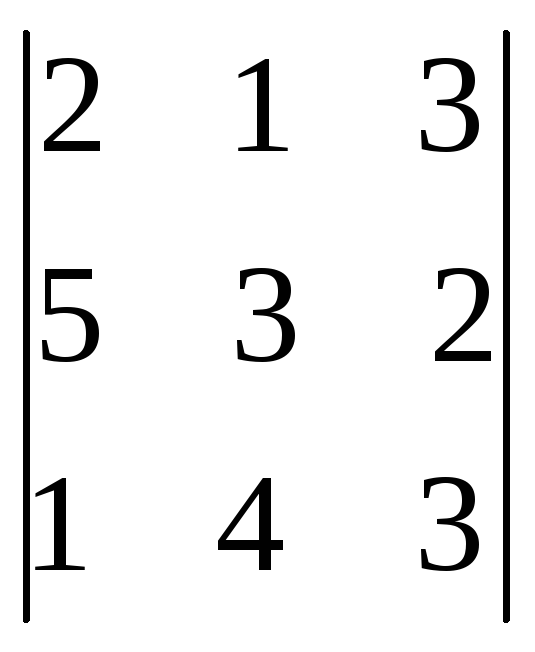 .
6.26.
.
6.26.
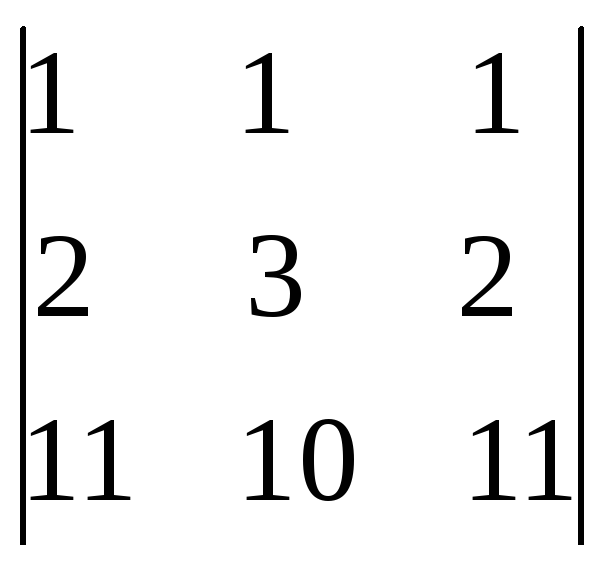 .
.
Вычислить определители разложением по какой-нибудь строке или столбцу.
6.27.
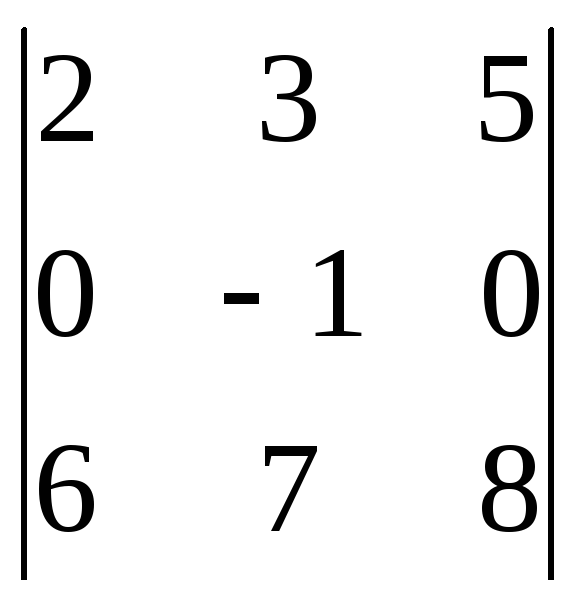 .
6.28.
.
6.28.
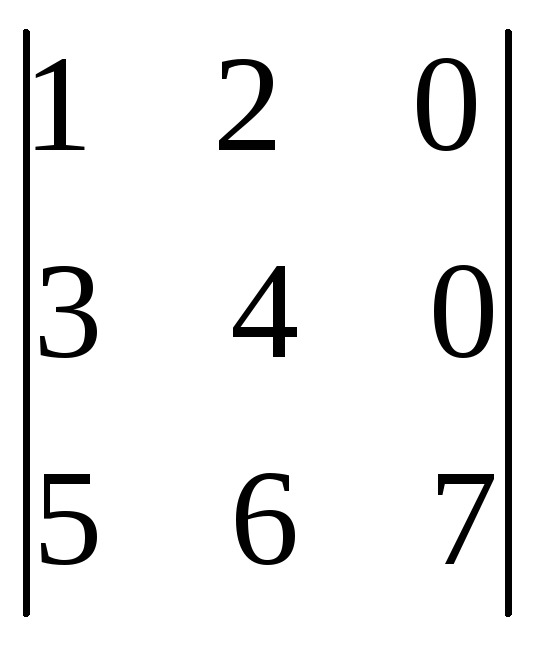 .
6.29.
.
6.29.
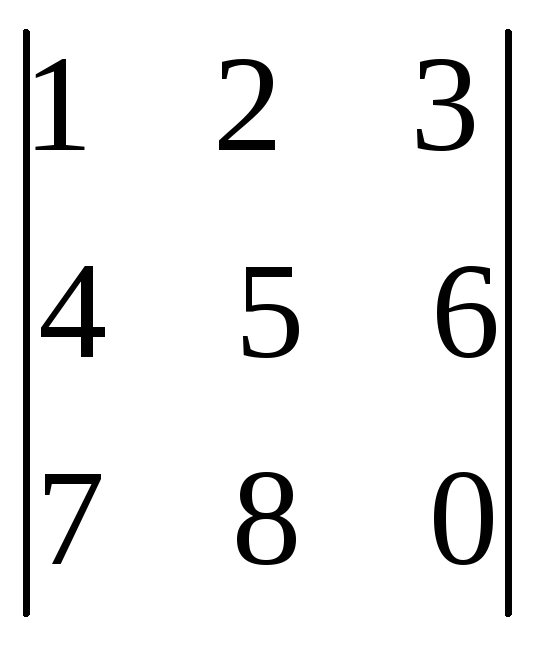 .
6.30.
.
6.30.
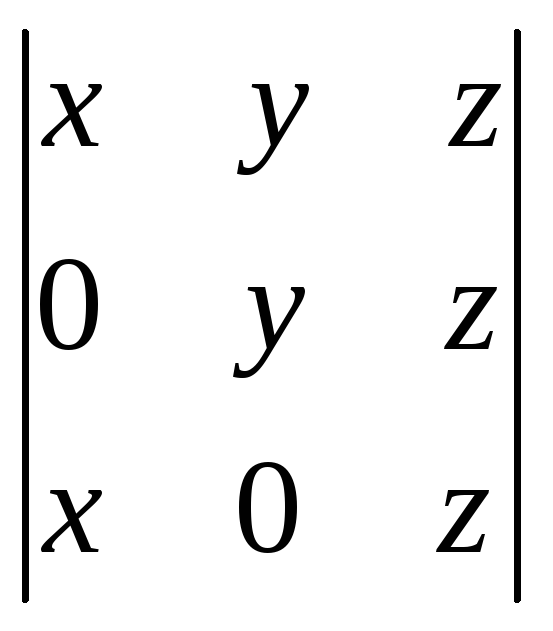 .
.
6.31.
 .
.
Решить уравнения и неравенство.
6.32.
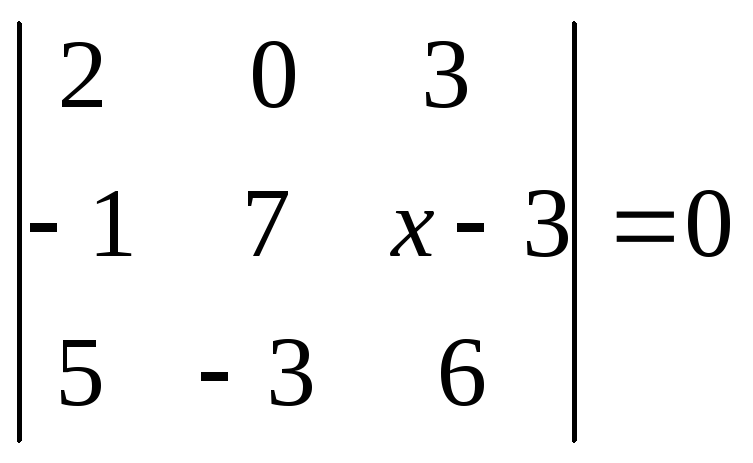 .
6.33.
.
6.33.
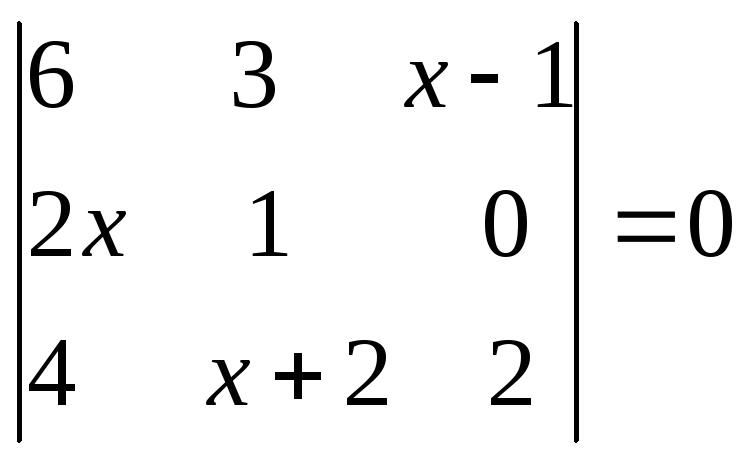 .
6.34.
.
6.34.
 .
.
Вычислить определители.
6.35.
 .
6.36.
.
6.36.
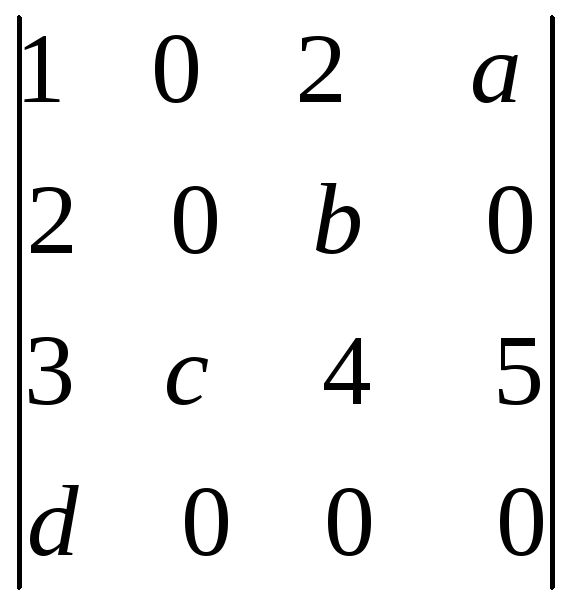 .
6.37.
.
6.37.
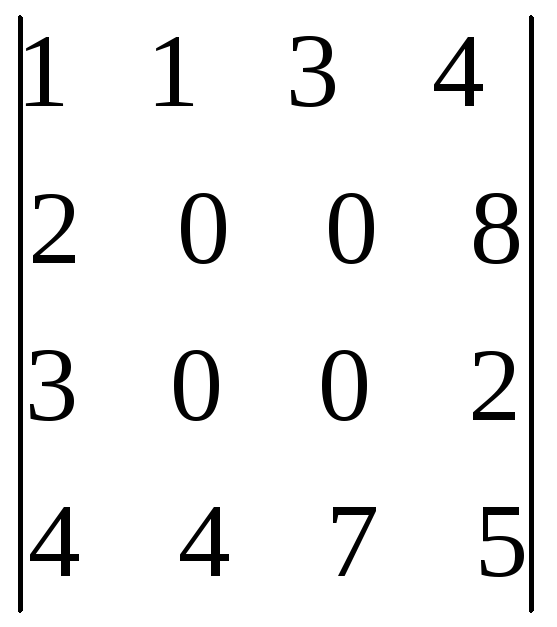 .
.
6.38.
 .
6.39.
.
6.39.
 .
6.40.
.
6.40.
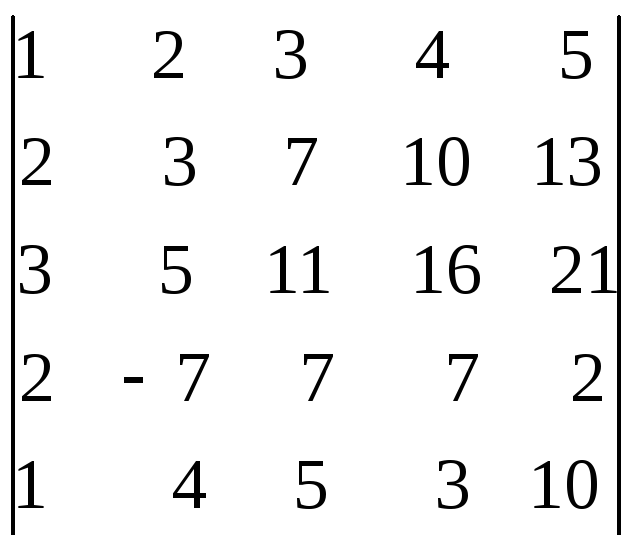 .
.
2. Задачи повышенного уровня сложности.
Вычислить определители.
6.41.
 .
6.42.
.
6.42.
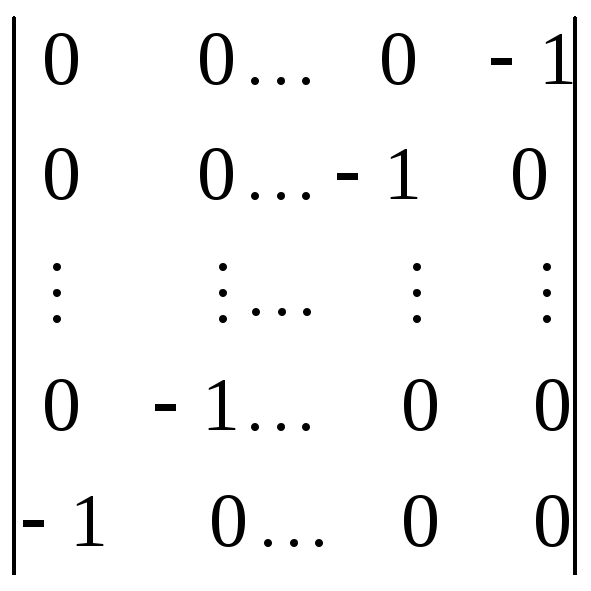 .
.
6.43.
 .
6.44.
.
6.44.
 .
.
Вычислить определители методом рекуррентных соотношений.
6.45.
 .
6.46.
.
6.46.
 .
.
6.47.
 .
.
6.48. Не вычисляя
определителей, показать, что они делятся
на
![]() :
:
а)
 ;
б)
;
б)
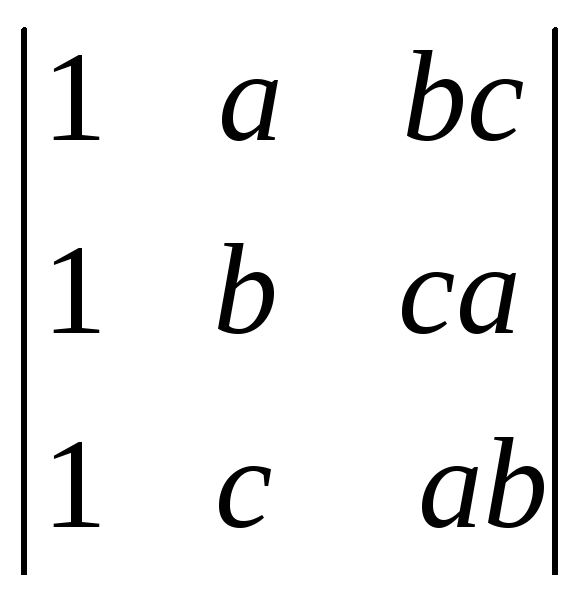 .
.
Вычислить, используя свойства определителей.
6.49.
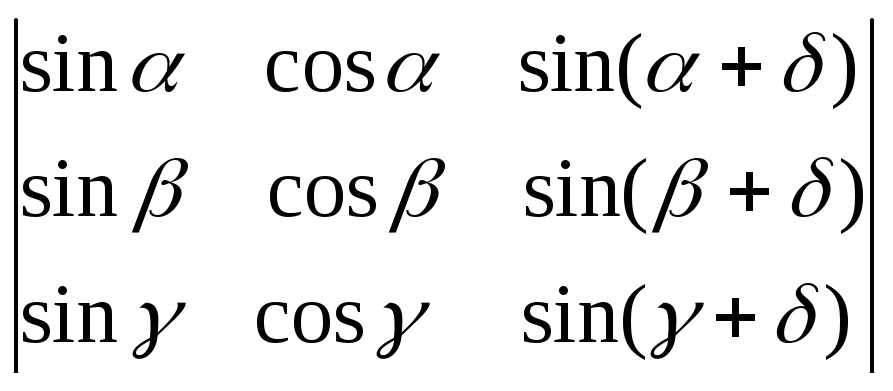 .
6.50.
.
6.50.
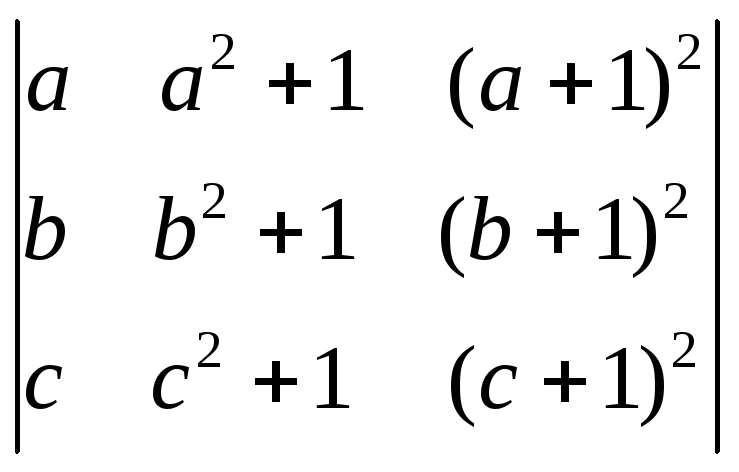 .
.
