СЕМИНАР 16
.docСЕМИНАР 16
Вычисление пределов функций с помощью замечательных пределов, получение асимптотических формул и применение их к вычислению пределов, непрерывность функции, классификация точек разрыва.
Вводная информация
Замечательные пределы.
Замечательными пределами являются:
первый замечательный предел
и второй замечательный предел
.
Асимптотические формулы.
Теорема. Если
,
то
,
где
,
т.е. функция
является бесконечно малой функцией при
.
Верно и обратное утверждение: если
,
где
- бесконечно малая функция при
,
то
.
Рассмотрим первый
замечательный предел
.
Тогда
,
при этом
.
Используя полученную формулу, представим
функцию
в виде
.
Так как
(действительно
),
перепишем найденную формулу в виде
.
Подобные формулы, которые называют асимптотическими формулами
(или асимптотическими разложениями, или асимптотическими представлениями функций), можно получить для многих функций. Для простейших элементарных функций справедливы оценки:
1)
;
2)
;
3)
,
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
.
Эти формулы удобно
использовать при нахождении пределов
функций вида
.
Непрерывность функции.
Определение.
Функция
называется непрерывной
в точке
,
если
.
Приведем эквивалентное
определение. Функция
называется непрерывной
в точке
,
если: 1) она определена в точке
;
2)
такое, что при
.
Определение.
Точка
,
в которой функция
не является непрерывной, называется
точкой
разрыва этой
функции.
Определение.
Точка
называется точкой
разрыва первого рода функции
,
если существуют конечные односторонние
пределы
и
и выполняются условия: 1)
или 2)
.
Разность
называется скачком
функции
в точке
.
Точка разрыва первого рода, удовлетворяющая
условию 2), называется точкой устранимого
разрыва
(разрыв устраняется переопределением
значения функции в этой точке
).
Определение.
Точку
называют точкой
разрыва второго рода,
если в этой точке имеется разрыв функции,
не являющийся разрывом первого рода.
ЗАДАЧИ
1. Задачи удовлетворительного уровня сложности.
Вычислить пределы, используя первый замечательный предел.
16.1
.
16.2.
.
16.3.
.
16.4.
.
16.5.
.
16.6.
.
16.7.
.
16.8.
.
16.9.
.
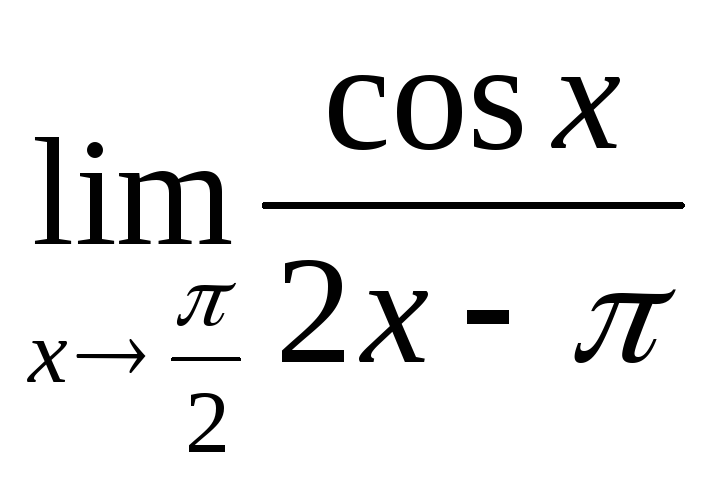16.10.
.
16.11.
.
16.12.
.
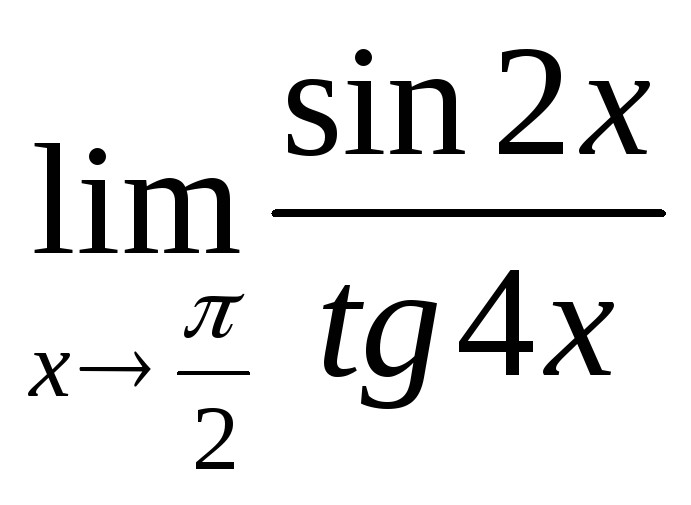16.13.
.
16.14.
.
16.15.
.
16.16.
.
16.17.
.
16.18.
.
2. Вычислить пределы, используя второй замечательный предел.
16.19.
.
16.20.
.
16.21.
.
16.22.
.
16.23.
.
16.24.
.
16.25.
.
16.26.
.
16.27.
.
16.28. Вычислить
предел
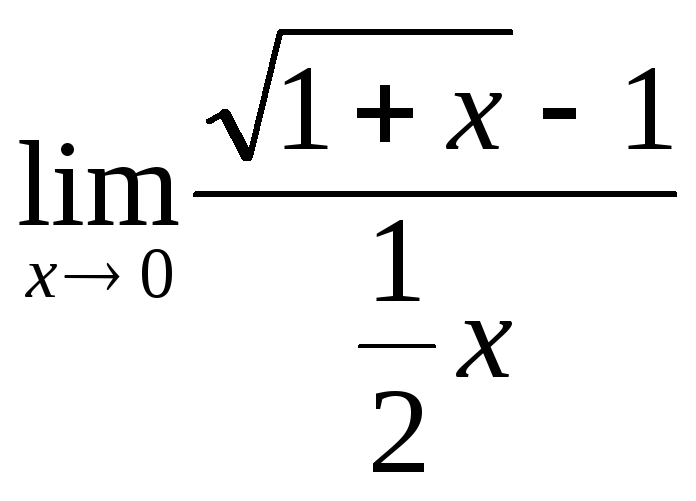и, используя результат вычисления, найти
асимптотическую формулу для функции
.
16.29. Вычислить
предел
и, используя результат вычисления,
найти асимптотическую формулу для
функции
.
16.30. Вычислить
предел
и, используя результат вычисления, найти
асимптотическую формулу для функции
.
16.31. Вычислить
предел
и, используя результат вычисления, найти
асимптотическую формулу для функции
.
16.32. Вычислить
предел
и, используя результат вычисления, найти
асимптотическую формулу для функции
.
Используя асимптотические формулы вычислить пределы.
16.33.
.
16.34.
.
16.35.
.
16.36.
.
16.37.
.
16.38.
.
16.39.
.
16.40.
.
16.41.
.
16.42.
.
16.43.
.
16.44.
.
16.45.
.
16.46.
.
16.47.
Исследовать на непрерывность функции. Определить род точек разрыва при их наличии.
16.48.
.
16.49.
.
16.50.
.
16.51.
.
16.52.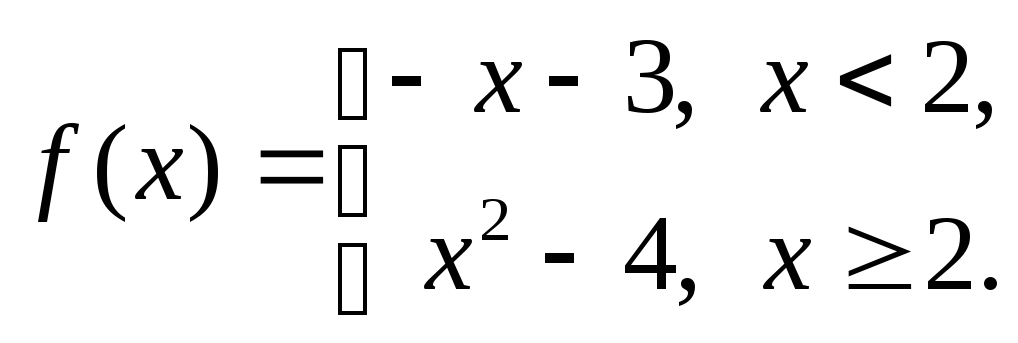
16.53.
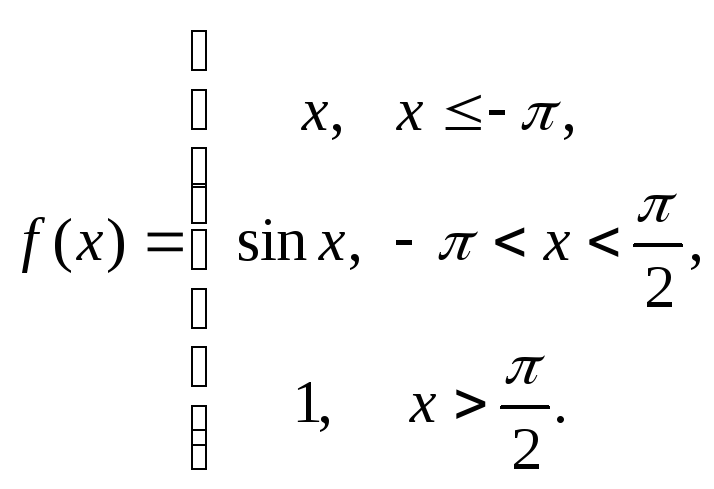16.54.
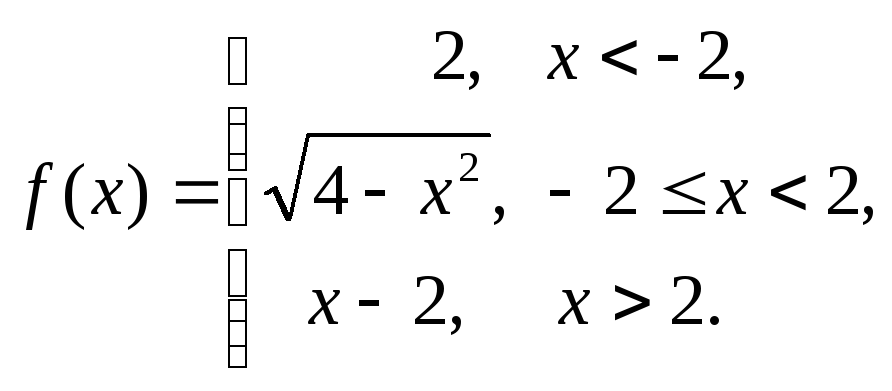
16.55.
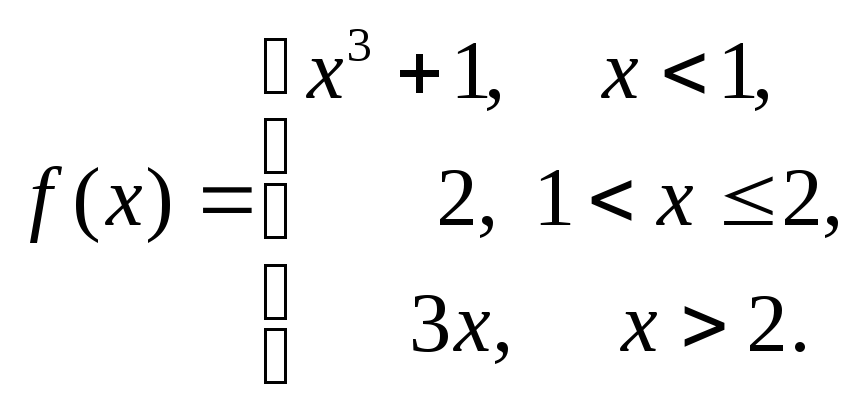16.56.
.
16.57.
.
16.58.
.
16.59.
.
16.60
.
2. Задачи повышенного уровня сложности.
Вычислить пределы, используя первый замечательный предел.
16.61.
.
16.62.
.
16.63.
.
16.64.
.
16.65.
.
16.66.
.
Вычислить пределы, используя второй замечательный предел.
16.67.
.
16.68.
.
16.69.
.
16.70.
.
16.71.
.
16.72. Вычислить
предел
и, используя результат вычисления, найти
асимптотическую формулу для функции
.
16.73. Вычислить
предел
и, используя результат вычисления, найти
асимптотическую формулу для функции
.
16.74. Вычислить
предел
и, используя результат вычисления, найти
асимптотическую формулу для функции
.
Используя асимптотические формулы вычислить пределы.
16.75.
.
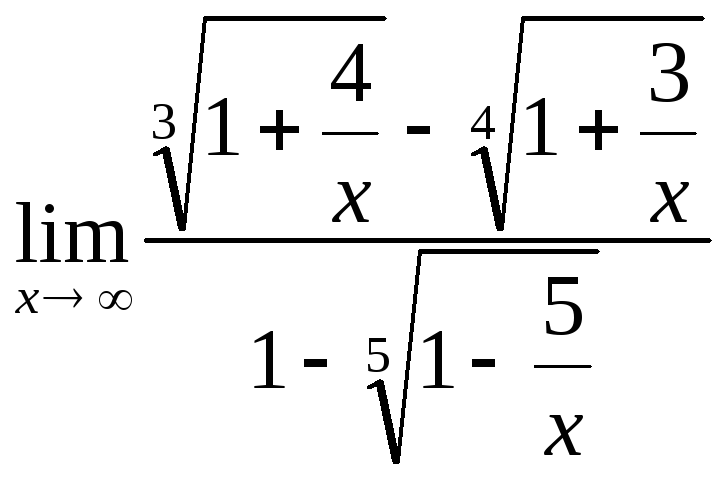16.76.
.
16.77.
.
16.78.
.
6.79.
.
16.80.
.