Лабораторная работа № 3. Исследование электрической схемы замещения магнитной цепи

ЦЕЛЬ РАБОТЫ: ознакомиться с методом математического моделирования магнитных цепей в электромеханических устройствах с использованием электрических схем замещения.

3.1. Теоретическая часть

Электромагнитное поле в общем случае описывается системой уравнений Максвелла, которая в дифференциальной форме выглядит следующим образом:

_(3.1)

Здесь – вектор напряженности магнитного поля, А/м;– вектор индукции магнитного поля, Тл;– вектор напряженности электрического поля, В/м;– вектор электростатической индукции, Кл/м²;– вектор плотности тока;σ– удельная проводимость;ε– диэлектрическая проницаемость среды;ε₀– электрическая постоянная, Ф/м;μ– магнитная проницаемость среды;μ₀– магнитная проницаемость вакуума, Гн/м. Для линейной задачиσ = const, ε = const, μ = const.

Статическое магнитное поле является частным случаем электромагнитного поля и описывается системой уравнений

_(3.2)

В интегральной форме данная система уравнений принимает вид

_(3.3)

Здесь первое уравнение представляет собой закон полного тока: циркуляция вектора по замкнутому контуруlравна полному току, охваченному данным контуром, который может вычисляться как интеграл от плотности токапо площади контураSили как сумма токовI_jвNпроводниках, охваченных контуром.

Во многих случаях в электромеханических системах закон полного тока может быть представлен в форме

, (3.4)

где H_i– касательная проекция вектора напряженности магнитного поля на участке длинойl_i;I– ток в обмотке с количеством витковW;F– намагничивающая сила обмотки.

Проведем преобразования:

. (3.5)

Получаем закон Ома для магнитной цепи:

, (3.6)

где F– магнитодвижущая сила магнитной цепи;

–магнитный поток на i-м участке магнитной цепи;

– магнитное сопротивлениеi-го участка магнитной цепи;λ =μ₀μ– удельная магнитная проводимость участка магнитной цепи;l– длина участка магнитной цепи;S– сечение участка магнитной цепи.

Следует отметить, что магнитное сопротивление вычисляется по формуле, изоморфной с формулой электрического сопротивления.

Выясним, при каких условиях электрическая и магнитная цепи подобны. Для этого воспользуемся первой теоремой подобия. Для определения условий, критериев и масштабов подобия выполним определенные действия в следующем порядке:

1. Определим соответствие величин оригинала и модели:

. (3.7)

2. Введем масштабы подобия:

. (3.8)

3. Приведем уравнения тепловых и электрических процессов к безразмерному виду:

; (3.9)

. (3.10)

4. Подставим в уравнение (3.10) величины из уравнения (3.9) с соответствующими масштабными коэффициентами:

. (3.11)

5. Уравнение (3.9) тождественно уравнению (3.11) при выполнении условия

_.. (3.12)

6. На основании (3.12) получим выражение критерия подобия

. (3.13)

7. Проведем анализ размерностей величин, входящих в уравнение оригинала (3.9):

(3.14)

Видим, что размерности всех шести величин могут быть построены из двух основных размерностей: Вб, А. Это значит, что из трех масштабов подобия два масштаба являются независимыми, то есть их значения можно выбрать произвольным образом, а один – является зависимым. В качестве зависимого удобнее всего выбрать масштаб. Остальным масштабамm_Rиm_F можно присвоить любые произвольные значения. В целях упрощения модели величины сопротивлений и МДС можно выбрать равными соответствующим величинам тепловых сопротивлений и ЭДС, то естьm_R= m_F = 1.

Зависимый масштаб должен быть рассчитан из (3.12):

. (3.15)

Следует отметить, что подобие магнитной и электрической цепей распространяется и на случай разветвленных магнитных цепей, где в качестве ветвей магнитной цепи выступают участки магнитопровода.

В простейшем случае при построении электрической схемы замещения магнитной цепи исследуемый магнитопровод разбивается вдоль силовой линии магнитного поля на участки с разным значением магнитного сопротивления (рис. 3.1, а). Каждый участок заменяется магнитным сопротивлением R_m, которому в соответствие ставится электрическое сопротивлениеR, связанное с магнитным сопротивлением соотношением (3.10). Обмотке с намагничивающей силойFв электрической схеме замещения соответствует ЭДСE(рис. 3.1, б).

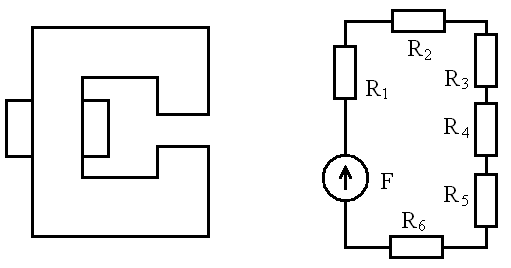
Рис. 3.1. Магнитная система реактора (а) и ее упрощенная электрическая схема замещения (б)

В более точных моделях массивные участки магнитопровода моделируются электрической сеткой, построенной из электрических сопротивлений, каждый из которых соответствует определенному участку м

Рис. 3.2. Элемент электрической сетки

агнитопровода и определенному направлению магнитного потока. Наибольшее распространение получили сетки с прямоугольными ячейками (рис. 3.2). Каждое электрическое сопротивление соответствует магнитному сопротивлениюi-го прямоугольного участка длинойΔl_i, сечениемΔS_i, вычисляемому как. Например, сопротивления, изображенные на рис. 3.2, рассчитываются как

, ,

, , (3.16)

где l_δ– расчетная длина зазора (машины) в осевом направлении.

Магнитодвижущая сила обмотки в этом случае распределяется равномерно по вертикальным участкам сердечника полюса, охваченного катушкой возбуждения.

Уточненная электрическая схема замещения магнитной цепи машины постоянного тока (МПТ) изображена на рис. 3.3.

В результате расчета электрической схемы замещения, изображенной на рис. 3.3, получаем токи в сопротивлениях, которые пересчитываются в магнитные потоки на соответствующем участке магнитопровода:

. (3.17)

Величину индукции можно рассчитать на участках, соответствующих магнитным сопротивлениям. При этом на сопротивлениях с индексом x(на рис. 3.2 – этоR_mx1иR_mx1) рассчитываются составляющие индукции по осиx иy:

и ,

и , (3.18)

где Ф_xi,Ф_yi– величина магнитного потока вi-м магнитном сопротивлении.

Значения электрических потенциалов в узлах сетки пересчитываются в значения скалярного магнитного потенциала:

. (3.20)