
- •Московский государственный строительныйуниверситет
- •§2. Некоторые свойства пределов функций
- •§3. Эквивалентные функции
- •§4. Таблица эквивалентных функций при X→0
- •§5. Свойства бесконечно малых функций
- •§6. Непрерывность функции в точке
- •§7. Вычисление предела функции в точке
- •§7. Вычисление предела функции при X→∞
§2. Некоторые свойства пределов функций
Пусть: Cпостоянное число,
предел функции f(x)
существует в точкеa,![]() ,
,
предел функции g(x)
существует в точкеa,![]() .
.
Тогда:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
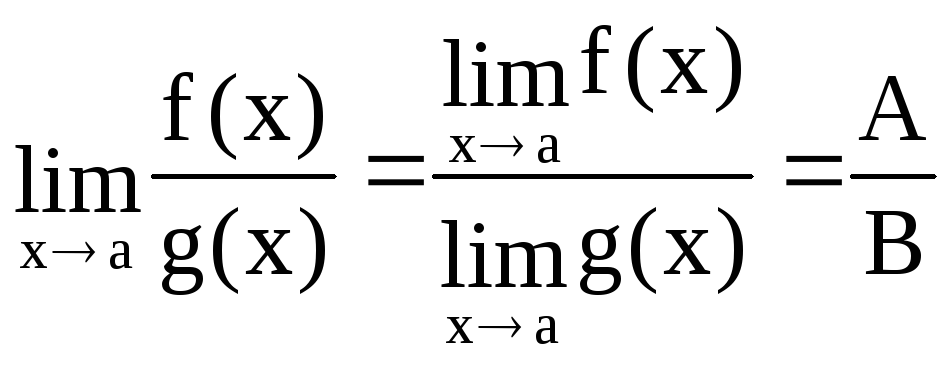 ,
если
,
если![]() .
.
Предел постоянной величины равен
значению этой величины. При вычислениях,
константу можно и рекомендуется выносить
за знак предела. В условии, когда функции
f(x) иg(x)
имеют конечные пределы в точке, функцииf(x)+g(x),f(x)∙g(x)
также имеют пределы в этой точке. При
дополнительном условии![]() ,
существует предел функцииf(x)/g(x).
,
существует предел функцииf(x)/g(x).
Указанные свойства пределов функций будут соответственно справедливы в точке aслева (x→a–o), в точкеaсправа (x→a+o), приx→–∞ и приx→+∞.
§3. Эквивалентные функции
Определение 7.
Функции f(x)
и g(x)
называются эквивалентными при
x→a,
если
![]() .
.
В этом случае пишут f(x) ~g(x) приx→aи говорят, что приx→aфункцияf(x) асимптотически ведет себя как функцияg(x) и наоборот, функцияg(x) асимптотически ведет себя как функцияf(x). При вычислении пределов с использованием эквивалентных функций применяют следующие теоремы:
1. Пусть f(x)
~g(x) приx→a, тогда![]() ,
если один из этих пределов существует.
,
если один из этих пределов существует.
2. Пусть f(x)
~f1(x)
иg(x) ~g1(x)
приx→a,
тогда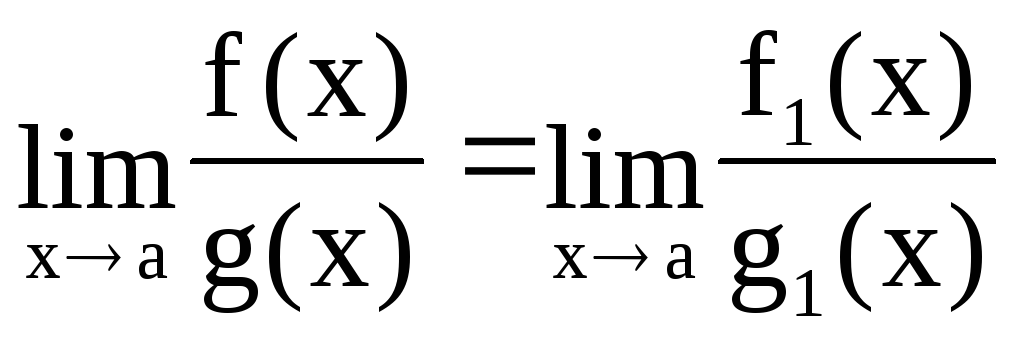 ,
если один из этих пределов существует.
,
если один из этих пределов существует.
Можно сравнивать функции f(x)
иg(x) в точкеaслева (x→a–o),
в точкеaсправа (x→a+o),
приx→–∞ и приx→+∞,
при этом вычисляют пределы в соответствующих
предельных точках. Например, если![]() ,
то говорят, что функцииf(x)
иg(x)
эквивалентны в точкеaслева и приx→a–oфункцияf(x)
асимптотически ведет себя как функцияg(x). Если
,
то говорят, что функцииf(x)
иg(x)
эквивалентны в точкеaслева и приx→a–oфункцияf(x)
асимптотически ведет себя как функцияg(x). Если![]() ,
то говорят, что функцииf(x)
иg(x)
эквивалентны приx→+∞ и
пишутf(x) ~g(x) приx→+∞.
,
то говорят, что функцииf(x)
иg(x)
эквивалентны приx→+∞ и
пишутf(x) ~g(x) приx→+∞.
§4. Таблица эквивалентных функций при X→0
1. sin(x) ~ x; 6. ax
~ 1+x∙ln(a); 11. sh(x) ~ x, ![]() ;
;
2. cos(x) ~ ![]() ; 7.
ex ~
1+x; 12. ch(x) ~
; 7.
ex ~
1+x; 12. ch(x) ~ ![]() ,
,
![]() ;
;
3. tg(x) ~ x; 8. loga(1+x)
~
![]() ; 13.
th(x) ~ x,
; 13.
th(x) ~ x,![]() ;
;
4. arcsin(x) ~ x; 9. ln(1+x) ~ x;
5. arctg(x) ~ x; 10. (1+x)α ~ 1+α∙x.
§5. Свойства бесконечно малых функций
Определение 8.
Функция α(x)
называется бесконечно малой при
x→a,
если
![]() .
.
При вычислении пределов применяют следующие свойства бесконечно малых функций:
1. Сумма конечного числа бесконечно малых функций при x→aесть функция бесконечно малая.
2. Произведение бесконечно малой функции α(x) на ограниченную функциюz(x) приx→aесть функция бесконечно малая.
Следствия: а) произведение бесконечно малых функций есть функция бесконечно малая;
б) произведение бесконечно малой функции на константу есть функция бесконечно малая;
в) частное от деления бесконечно малой функции на ограниченную функцию, предел и значения которой отличены от нуля, есть функция бесконечно малая.
3. Пусть α(x)
– бесконечно малая функция приx→aи не обращается в нуль, тогда функция![]() – бесконечно большая приx→a.
– бесконечно большая приx→a.
Соответственно определяются бесконечно малые функции в точке aслева (x→a–o), в точкеaсправа (x→a+o), приx→–∞ и приx→+∞.
§6. Непрерывность функции в точке
Определение 9.
Функция f(x)
называется непрерывной в точке
x0,
если
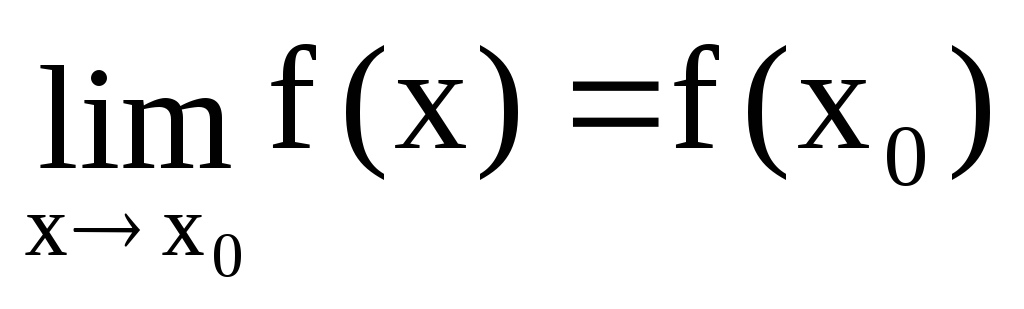 .
.
![]()
Определение 10.
Функция f(x)
называется непрерывной в точке
x0,
если
![]() ,
гдеΔx=x–x0
и Δf=f(x)–f(x0).
,
гдеΔx=x–x0
и Δf=f(x)–f(x0).
![]()
Определение 11.
Функция f(x)
называется непрерывной в точке
x0,
если
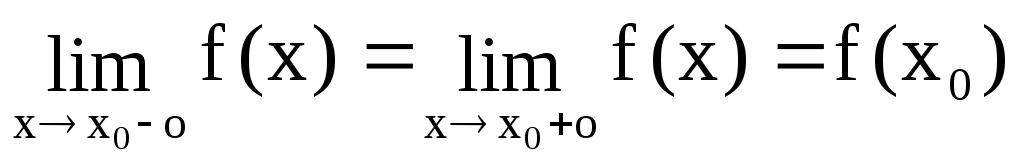 .
.
Определения 9, 10 и 11 эквивалентны.
Точка x0это конечное число, которое принадлежит области определения функцииf(x). Нет смысла задаваться вопросом о непрерывности функции приx→–∞ и приx→+∞. Однако, явление непрерывности функцииf(x) в точкеx0слева и в точкеx0справа существует.
Определение 12.
Функция f(x)
называется непрерывной в точке
x0
слева, если
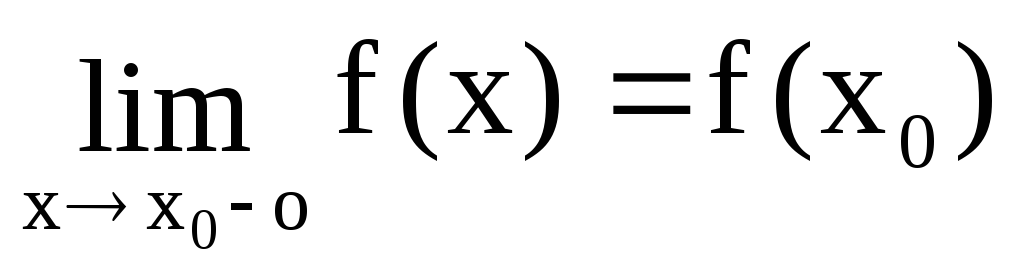 .
В этом случае
.
В этом случае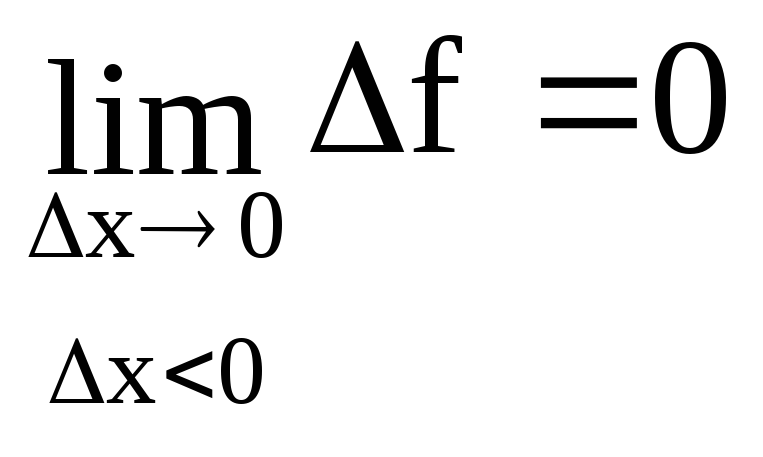 .
.
Определение 13.
Функция f(x)
называется непрерывной в точке
x0
справа, если
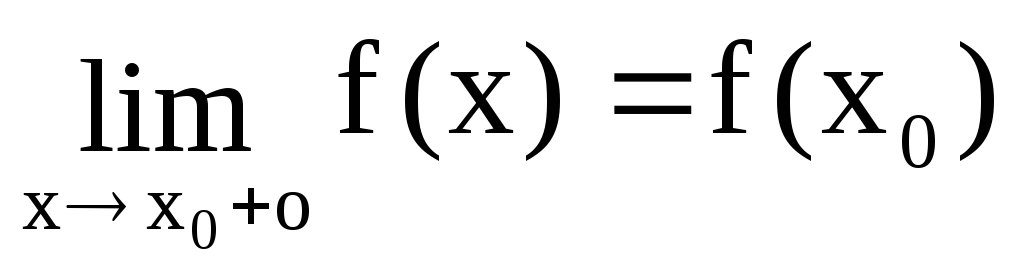 .
В этом случае
.
В этом случае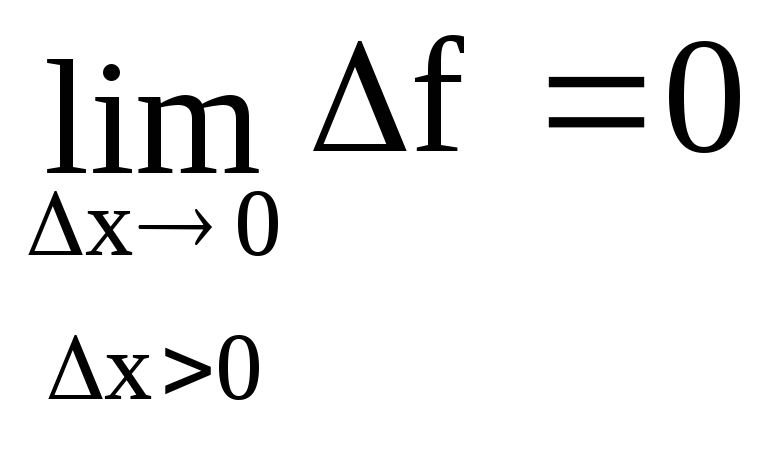 .
.
Некоторые свойства непрерывных в точке функций:
1) Пусть: f(x)
непрерывна в точкеx0,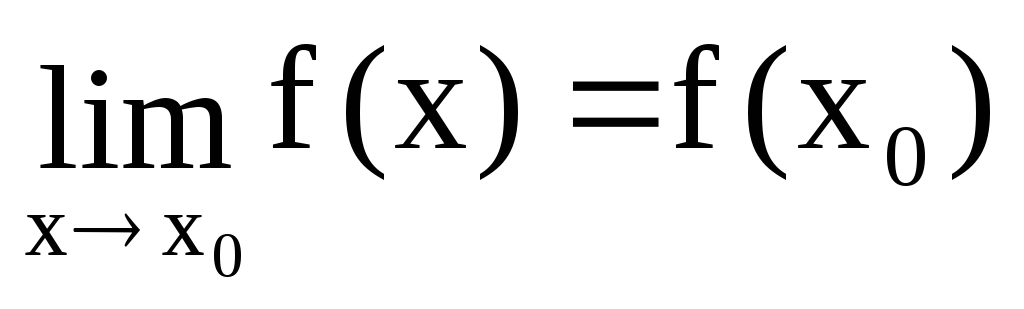 ;
;
g(x)
непрерывна в точкеx0,![]() .
.
Тогда:
![]() непрерывна в точкеx0,
непрерывна в точкеx0,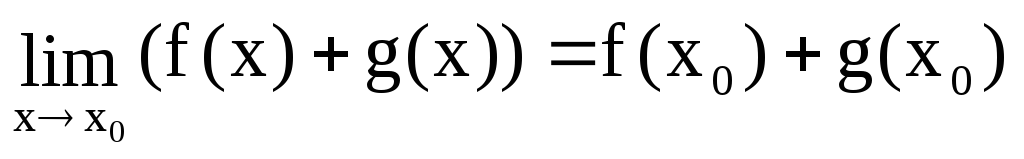 ;
;
![]() непрерывна в точкеx0,
непрерывна в точкеx0,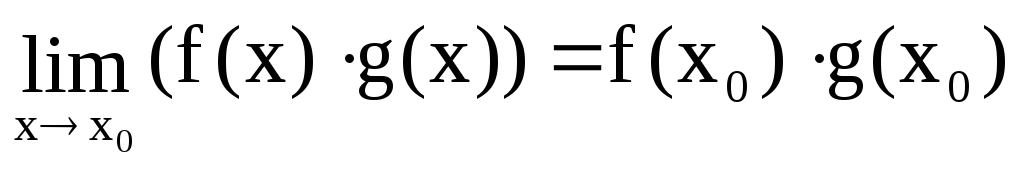 ;
;
![]() непрерывна в точкеx0(при условии
непрерывна в точкеx0(при условии![]() ),
),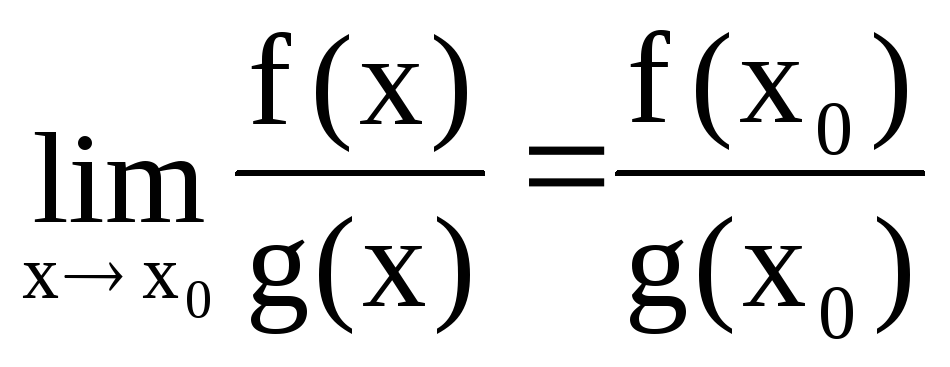 .
.
2) Если: g(y) непрерывна в точкеy0,
f(x) непрерывна в точкеx0и
y0=f(x0),
тогда функция g(f(x)) непрерывна в точкеx0.
3)
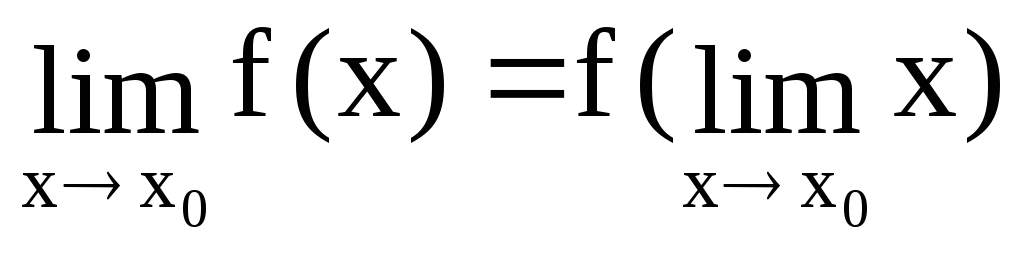 .
Это означает, что под знаком непрерывной
в точке функции можно переходить к
пределу.
.
Это означает, что под знаком непрерывной
в точке функции можно переходить к
пределу.
