§ 6. Теорема Кронекера – Капелли.

Теорема.Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг основной матрицы системы равнялся рангу ее расширенной матрицы

.

Пример 1.С помощью критерия Кронекера – Капелли определить, будут ли совместны следующие системы:

а) ;

б) .

Решение.

а) Вычисляем ранг матриц . Для этого путем элементарных алгебраических преобразований приведем матрицук ступенчатому виду :

.

1. Умножаем элементы 1-ой строки на «-3» и складываем с элементами 2-ой строки, затем умножаем элементы 1-ой строки на «-1» и складываем с элементами 3-ей строки.

2. Умножаем элементы 2-ой строки на «-1» и складываем с элементами 3-ей строки.

Число строк в полученной матрице равно 3, следовательно, согласно определению ранга матрицы (см. определение 3 §7 главы 1) имеем:

.

Аналогичным образом, получим

.

Т.к. , то в силу критерия Кронекера – Капелли, система решений не имеет (несовместна).

б) Составляем расширенную матрицу:

1. Меняем местами 1-ую и 2-ую строки.

2. Умножаем элементы 1-ой строки последовательно на «-2»; на «-1»; на «-5» и на «-3» и складываем соответственно с элементами 2-ой, 3-ей, 4-ой и 5-ой строк.

3. Умножаем элементы 2-ой строки последовательно на «-2»; «-3» и «-1» и складываем соответственно с элементами 3-ей, 4-ой и 5-ой строк.

4. Вычеркивая нулевые строки, получаем ступенчатую матрицу.

Число строк в полученной ступенчатой матрице равно 2 :

;;,

следовательно, система совместна.

Замечание.Для сокращения записи мы приводим к ступенчатому виду одновременно матрицы.

§ 7. Однородные системы линейных уравнений.

Определение 1. Система уравнений вида:

(I)

называется однородной.

Очевидно, что система (I) всегда имеет решение :

(нулевое решение). Таким образом, однородная система всегда совместна.

Теорема.Если в системе (I), то система (I) имеет единственное (следовательно, нулевое) решение, если определитель системы

,

и – бесчисленное множество решений (в том числе ненулевых), если

.

Замечание.Если в системе (I)(число уравнений меньше числа неизвестных), то система имеет бесчисленное множество решений.

Примеры.

Решить системы уравнений:

а) ;

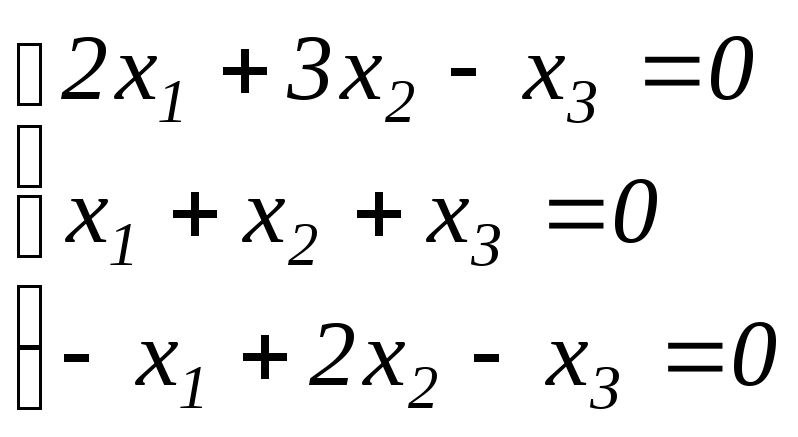б) .

Решение.

а) .

Мы сложили соответствующие элементы 2-ой и 3-ей строк. Система имеет единственное (нулевое) решение :

б) Решаем систему методом Гаусса (см. § 5).

.

Таким образом,

.

Система имеет бесчисленное множество решений. Давая различные значения, мы будем получать соответствующие решения заданной системы.

Например,

, тогда, получаем решение;

, тогда, получаем решение.

При подстановке в уравнения системы этих чисел, убеждаемся, что каждый раз мы получаем решение.

Глава 3. Примеры. Задание 1.

Даны определители:

,.

Вычислить:

а) определитель по правилу треугольников;

б) определитель разложением по элементам 2-го столбца;

в) определитель 4-го порядка .

Решение:

а)

б)

в) Для вычисления определителя 4-го порядка выберем строку (столбец), где больше нулей и, пользуясь свойством определителя (см. главу I §4 свойство 8), получим в этом столбце все нули, кроме, быть может, одного элемента. В нашем случае – это 3-ий столбец. Мысленно умножим элементы 1-ой строки на «-4» и сложим с элементами 2-ой строки, а затем умножим элементы 1-ой строки на «-2» и сложим с элементами 4-ой строки.

Мы разложили определитель 4-го порядка по элементам 3-его столбца (см. главу I §4 свойство 9). В этом разложении 3 последних слагаемых, очевидно, равны нулю. Таким образом, вычисление определителя 4-го порядка сводится к вычислению определителя 3-го порядка. Умножим элементы 1-ого столбца этого определителя на «-1» и сложим с элементами 2-ого столбца :

.

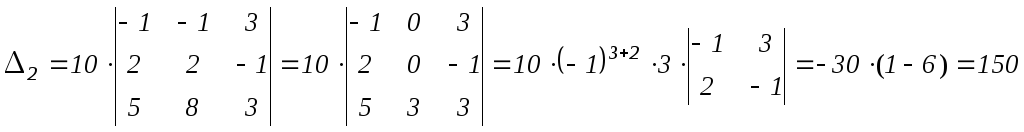Замечание 1.Следует обратить внимание на то, что та строка (столбец), которую мы умножаем, в определителе не изменяется. Меняется лишь та строка (столбец), к которой мы прибавляем результат умножения.

Например, в нашем определителе 3-го порядка 1-ый столбец, который мы умножаем на «-1», вошел в новый определитель без изменения, поменялся лишь 2-ой столбец.