
- •Московский государственный строительныйуниверситет
- •§ 2. Определители второго и третьего порядков.
- •§ 3. Определители n-ого порядка.
- •§4. Свойства определителей.
- •§5. Алгебра матриц.
- •Свойства суммы матриц и произведения матрицы на число.
- •Свойства умножения матриц.
- •§6. Обратная матрица.
- •§ 7. Ранг матрицы.
- •Глава 2. Системы линейных уравнений.
- •§1. Основные понятия.
- •§2. Матричная запись системы линейных уравнений.
- •§ 3. Решение системы линейных уравнений методом Крамера.
- •§ 4. Решение систем линейных уравнений с помощью обратной матрицы.
- •§ 5. Метод Гаусса.
- •§ 6. Теорема Кронекера – Капелли.
- •§ 7. Однородные системы линейных уравнений.
- •Примеры.
- •Глава 3. Примеры. Задание 1.
- •Задание 2.
- •Найти: а) ; б) ; в) ; г) ; д) .
- •Задание 3.
- •Ответ: , , .
- •Ответ: , , .
- •Задание 4.
- •Оглавление.
Московский государственный строительныйуниверситет
_
Кафедра высшей математики
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ И
ВЫПОЛНЕНИЮ РАСЧЕТНОГО ЗАДАНИЯ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
Москва 2007
С о с т а в и т е л и:
доцент, кандидат физико-математических наук Е.Е.Ассеева,
доцент Т.А.Мацеевич,
доцент, кандидат физико-математических наук И.Б.Раскина,
ассистент А.Н.Федосова .
ГЛАВА 1. МАТРИЦЫ.
§ 1. Основные понятия.
Определение 1.Матрицейразмерности![]() (читается
(читается![]() на
на![]() )
называется прямоугольная таблица чисел,
состоящая из
)
называется прямоугольная таблица чисел,
состоящая из![]() строк
и
строк
и![]() столбцов:
столбцов:
 .
.
Числа
![]() называютсяэлементами матрицы
называютсяэлементами матрицы![]() ,
индекс
,
индекс![]() указывает
номер строки, индекс
указывает
номер строки, индекс![]() -
номер столбца, на пересечении которых
находится элемент
-
номер столбца, на пересечении которых
находится элемент![]() .
Так, например, элемент
.
Так, например, элемент![]() стоит на пересечении четвертой строки
и пятого столбца.
стоит на пересечении четвертой строки
и пятого столбца.
Для обозначения матрицы используются следующие символы:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
Определение 2. Матрица![]() называетсяквадратной матрицей
называетсяквадратной матрицей ![]() -
ого порядка, если
-
ого порядка, если![]() (число
строк равно числу столбцов):
(число
строк равно числу столбцов):
 .
.
Элементы
![]() ,
где
,
где![]() ,
называютсядиагональными элементами
матрицы
,
называютсядиагональными элементами
матрицы![]() .
.
Определение 3. Квадратная матрица![]() называетсядиагональной,если
называетсядиагональной,если![]() (все элементы матрицы, за исключением,
быть может, диагональных, равны нулю):
(все элементы матрицы, за исключением,
быть может, диагональных, равны нулю):
 .
.
Определение 4. Диагональная матрица![]() называетсяединичной, если все ее диагональные
элементы равны единице (
называетсяединичной, если все ее диагональные
элементы равны единице (![]() ).
Единичная матрица обычно обозначается
буквой
).
Единичная матрица обычно обозначается
буквой![]() :
:
 .
.
Для обозначения единичной матрицы используют также символ Кронекера:
![]() символ
Кронекера.
символ
Кронекера.
Определение 5. Матрица называетсянулевой, если все ее элементы равны нулю:
 .
.
Матрицей – столбцомназывается
матрица![]() ,
состоящая из одного столбца (размерность
,
состоящая из одного столбца (размерность![]() ):
):
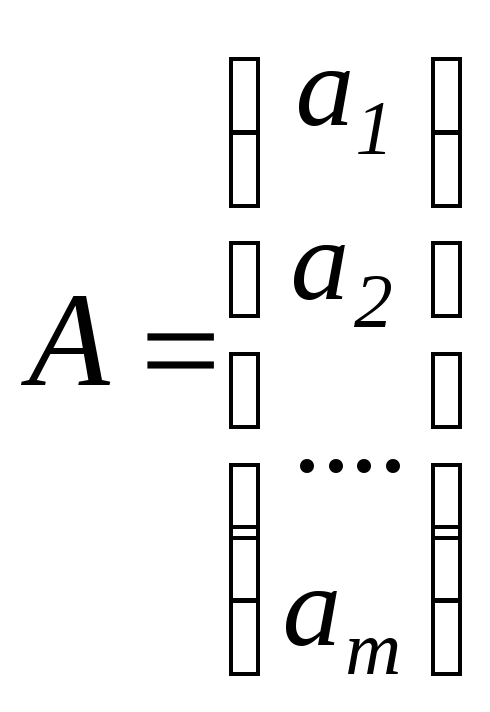 .
.
Матрицей – строкойназывается
матрица![]() ,
состоящая из одной строки (размерность
,
состоящая из одной строки (размерность![]() ):
):
![]() .
.
Определение 6. Две матрицы![]() и
и![]() называютсяравными, если
называютсяравными, если
1) размерности матриц совпадают;
2) соответствующие элементы матриц равны:
![]()
Пусть задана матрица
![]() размерности
размерности![]() .
Заменим 1-ую строку на 1-ый столбец, 2-ую
строку на 2-ой столбец и т.д.,
.
Заменим 1-ую строку на 1-ый столбец, 2-ую
строку на 2-ой столбец и т.д.,![]() -ую
строку на
-ую
строку на![]() -ый
столбец. Такая операция называетсятранспонированием матрицы
-ый
столбец. Такая операция называетсятранспонированием матрицы![]() .
.
Определение 7. Матрица, полученная
в результате транспонирования, называетсятранспонированнойпо отношению к
матрице![]() и
обозначается символом
и
обозначается символом![]() .
.
Пример. Транспонировать матрицу
![]() ,
,
 .
.
§ 2. Определители второго и третьего порядков.
Рассмотрим матрицу 2-го порядка:
 .
.
Этой матрице соответствует число,
которое называется определителем(детерминантом) матрицы![]() .
.
Для обозначения определителя используют символы:
![]() ,
,![]() .
.
Определение 1. Определителем 2-го
порядкаматрицы![]() называется
число:
называется
число:
![]() .
(1)
.
(1)
Например,
![]() .
.
Введем понятие определителя 3-го порядка. Пусть
 .
.
Определение 2. Минором элемента![]() матрицы
матрицы![]() называется
определитель, который получается из
матрицы
называется
определитель, который получается из
матрицы![]() вычеркиванием
вычеркиванием![]() -ой
строки и
-ой
строки и![]() -ого
столбца. Минор элемента
-ого
столбца. Минор элемента![]() обозначается символом
обозначается символом![]() .
.
Например, для элемента
![]() матрицы
матрицы![]() минором
служит определитель
минором
служит определитель
![]() .
.
Определение 3. Алгебраическим
дополнением![]() элемента
элемента![]() матрицы
матрицы![]() называется его минор, умноженный на
называется его минор, умноженный на![]() :
:
![]() .
(2)
.
(2)
В качестве примеравычислим алгебраическое дополнение
элемента![]() матрицы
матрицы
 .
.
В нашем случае
![]() ,
вычеркивая 2-ую строку и 1-ый столбец,
получим
,
вычеркивая 2-ую строку и 1-ый столбец,
получим
![]() ,
,![]() .
.
Определение 4. Определителем 3-го
порядка матрицы![]() называется
число
называется
число
 .
(3)
.
(3)
Поясним это определение на примере:
 ,
тогда
,
тогда
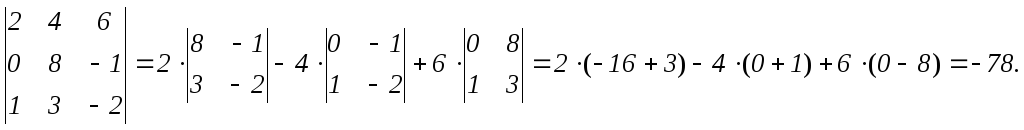
Для вычисления определителя 3-го порядка можно использовать, так называемое, «правило треугольника», а именно:

Например,
 .
.
