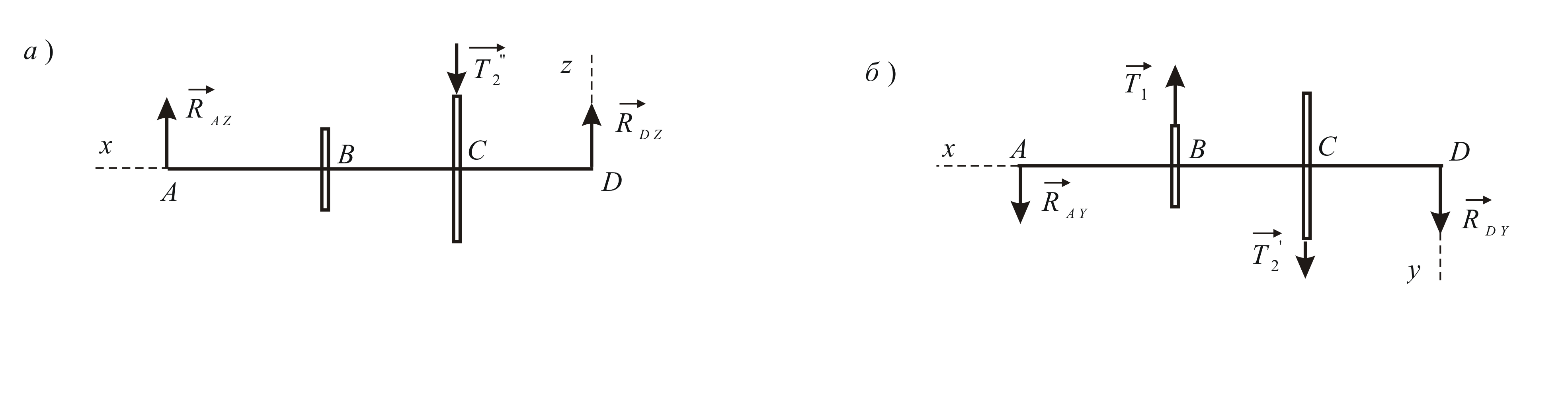4. Система сил в пространстве

Для равновесия произвольной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трёх взаимно перпендикулярных осей координат равнялась нулю и сумма моментов всех сил системы относительно каждой из этих осей равнялась нулю:

Проведём через точку , относительно которой вычисляется момент силы, какую-либо ось.

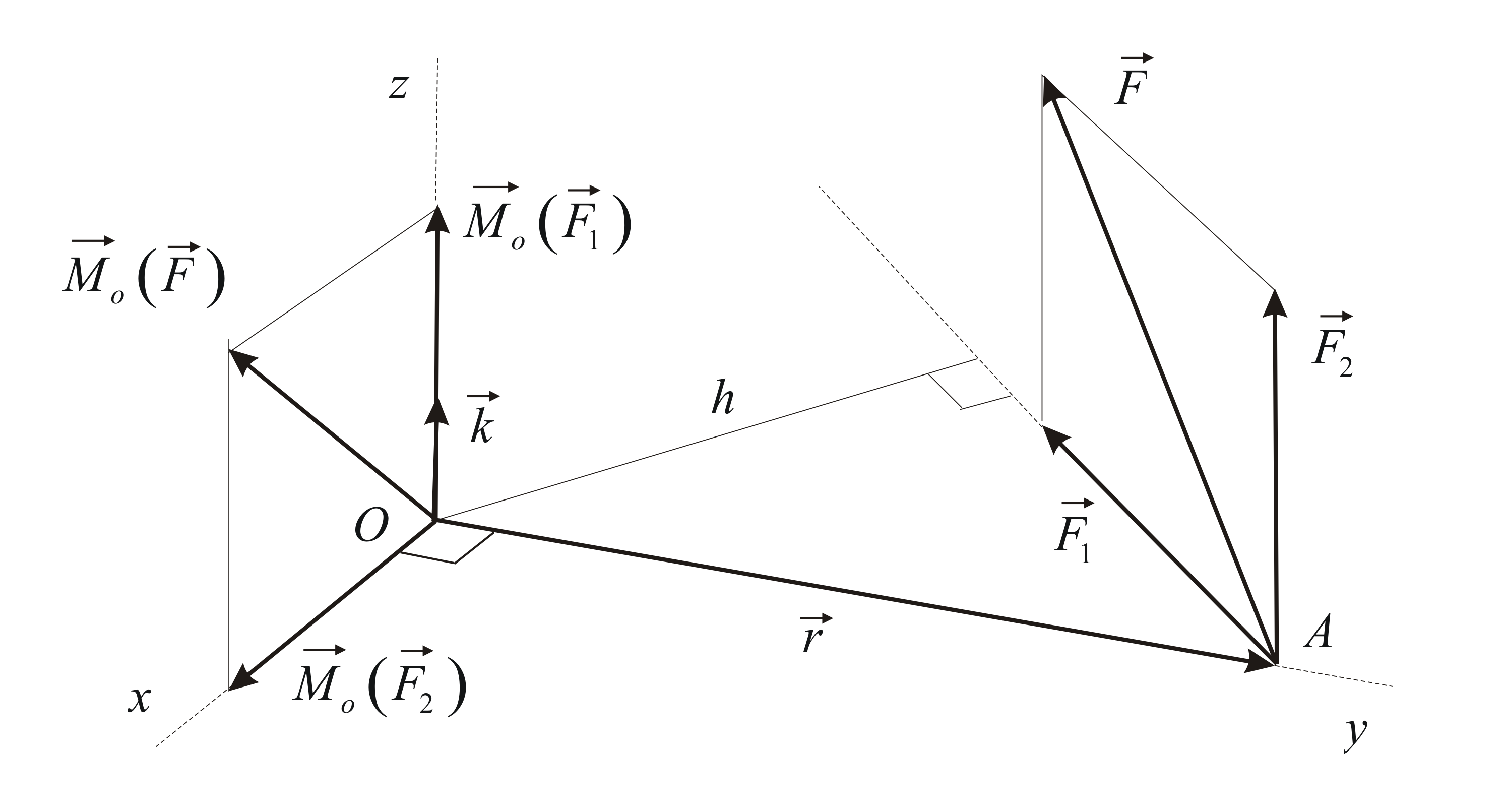
Моментом силы относительно оси называется проекция на ось вектора момента силы, вычисленного относительно любой точки этой оси.

Получим удобный для практических целей способ вычисления момента силы относительно оси. Рассмотрим силу , произвольным образом расположенную по отношению к оси. Проведём через точку приложения силы плоскость, перпендикулярную оси (Рис. 4.1). Пусть– точка пересечения этой плоскости с осью. Разложим силуна две составляющие, одна из которыхперпендикулярна оси, а втораяпараллельна оси:

.

Рис. 4.1

Умножая слева векторно на вектор , получаем:

.

Записывая последнее равенство в проекции на ось , получаем:

,

так как вектор перпендикулярен оси и не даёт на неё проекции.

Таким образом,

модуль момента силы относительно оси равен произведению модуля проекции силы на плоскость, перпендикулярную оси, на кратчайшее расстояние от оси до этой проекции. Момент силы относительно оси больше нуля, если с положительного конца оси поворот тела вокруг оси под действием силы виден против хода часовой стрелки и отрицателен в противоположном случае.

Заметим, что момент силы относительно оси равен нулю, если линия действия силы параллельна оси или пересекает ось. Другими словами, момент силы относительно оси равен нулю, если ось и линия действия силы лежат в одной плоскости (компланарны).

Пример 4.1.

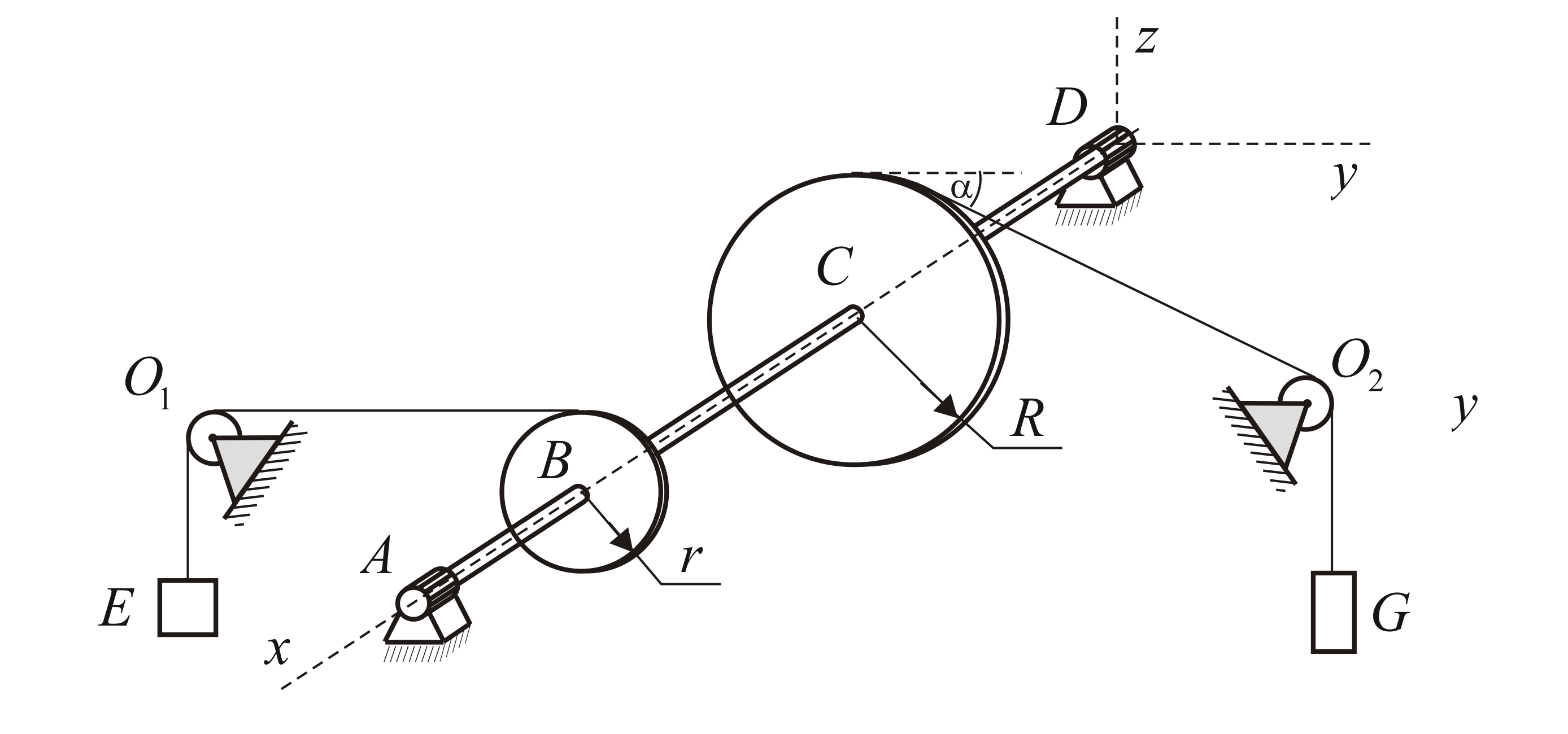
На горизонтальном валу жёстко закреплены два шкива, плоскости которых перпендикулярны валу. В точкахиустановлены цилиндрические шарниры. Намотанные на шкивы тросы переброшены через блокиии растягиваются грузамии(Рис. 4.2). Определить весгруза, при котором можно удержать в равновесии грузвесом. Определить также реакции шарниров. Трением пренебречь.

Рис. 4.2

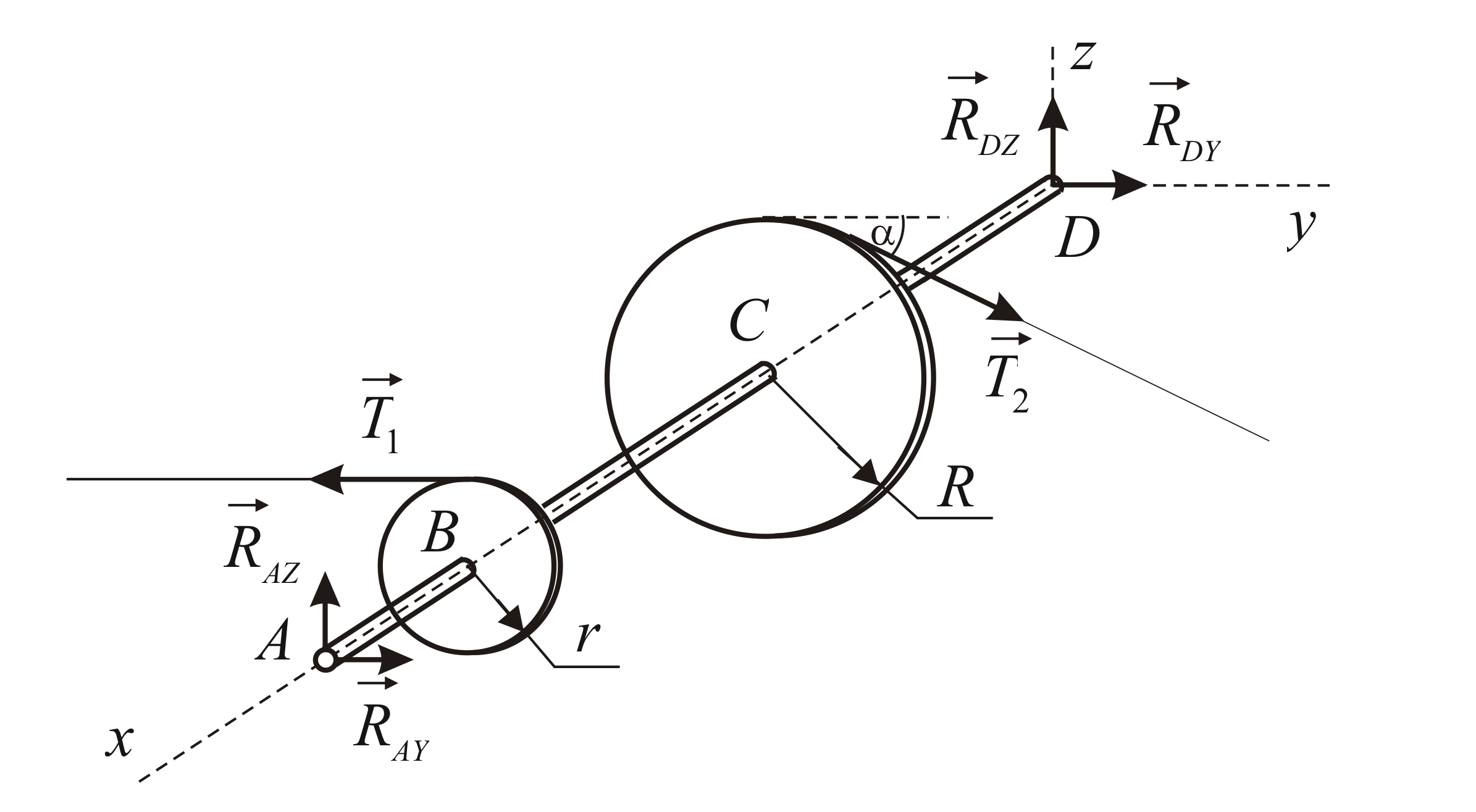
Рассмотрим равновесие вала . Силовая расчётная схема изображена на Рис.8.3. Заметим, что поскольку трение на блоках не учитывается, силы реакции тросов равны весу соответствующих грузов:;.

Рис. 4.3

Первые три из уравнений равновесия принимают вид:

При составлении уравнений моментов удобно использовать вспомогательные чертежи. Например, составляя уравнение моментов относительно оси , изобразим вид с положительного конца осина координатную плоскость(Рис. 4.4). В этом случае уравнение моментов относительно осисоставляется также, как для системы сил, расположенных в одной плоскости:

Рис. 4.4

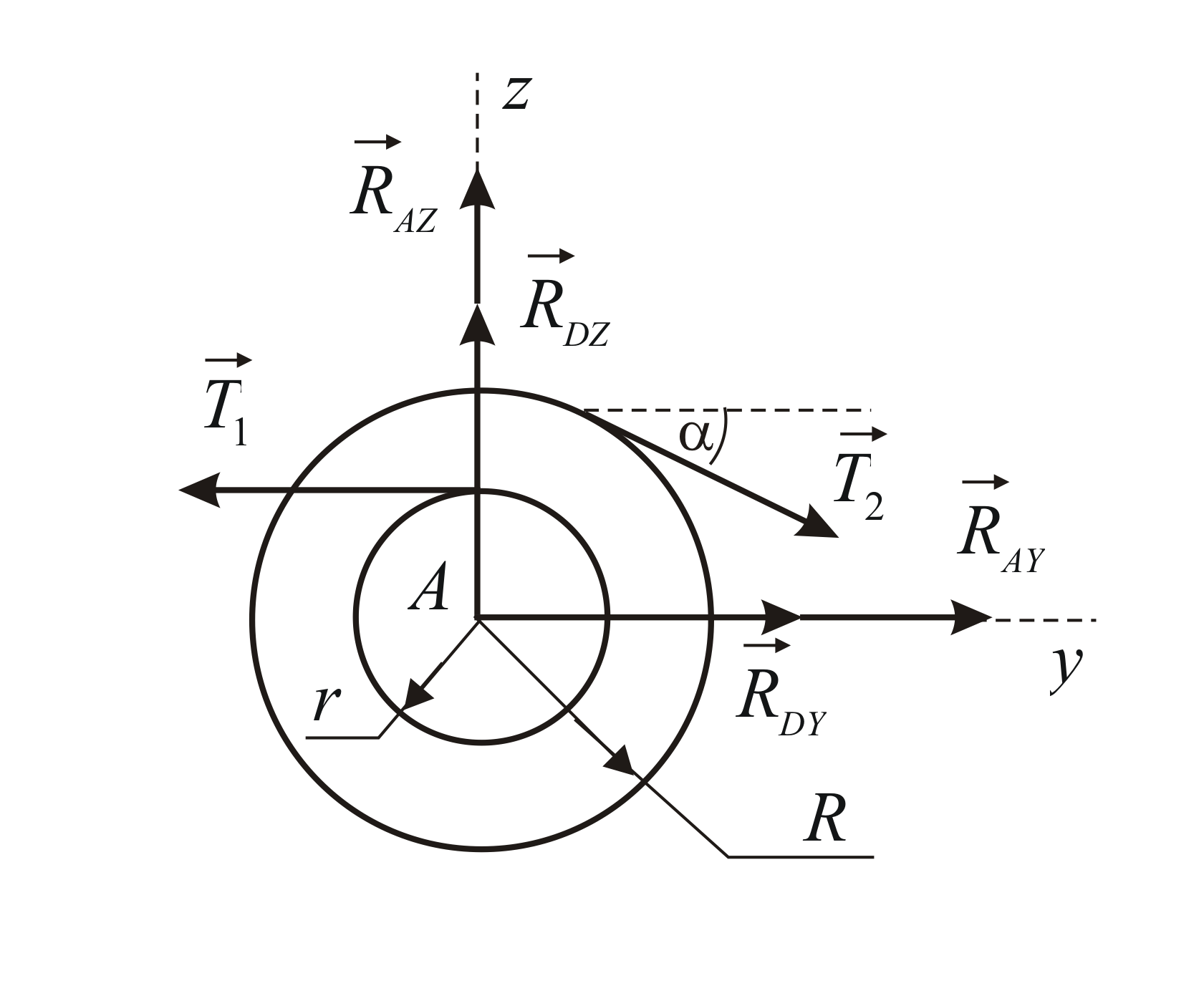
Составим уравнение моментов относительно оси (Рис. 4.5а). Заметим, что на таком чертеже силане видна, а силавидна частично – только её составляющая по оси().

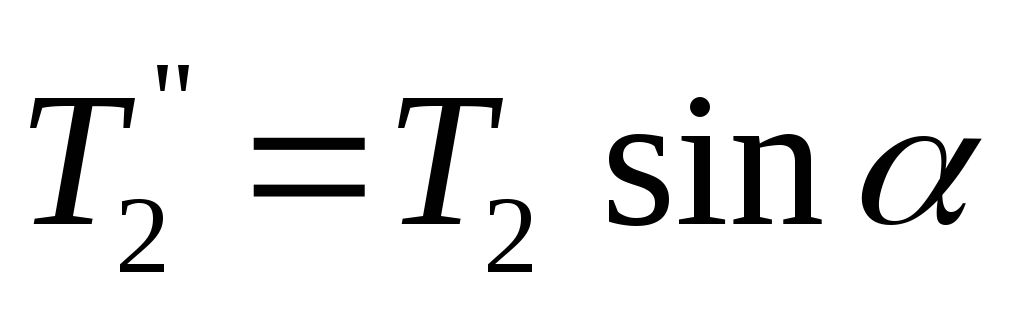Уравнение моментов относительно оси имеет вид (Рис. 4.5б):

Рис. 4.5

Полученная система уравнений позволяет определить все искомые силы по заданным размерам конструкции.

Заметим, что составлять вспомогательные чертежи не обязательно, но удобно, особенно при отсутствии соответствующих навыков. Другой приём, полезный при вычислении момента силы относительно оси, состоит в том, что сила раскладывается на составляющие, моменты которых достаточно просто вычисляются.

Пример 4.2

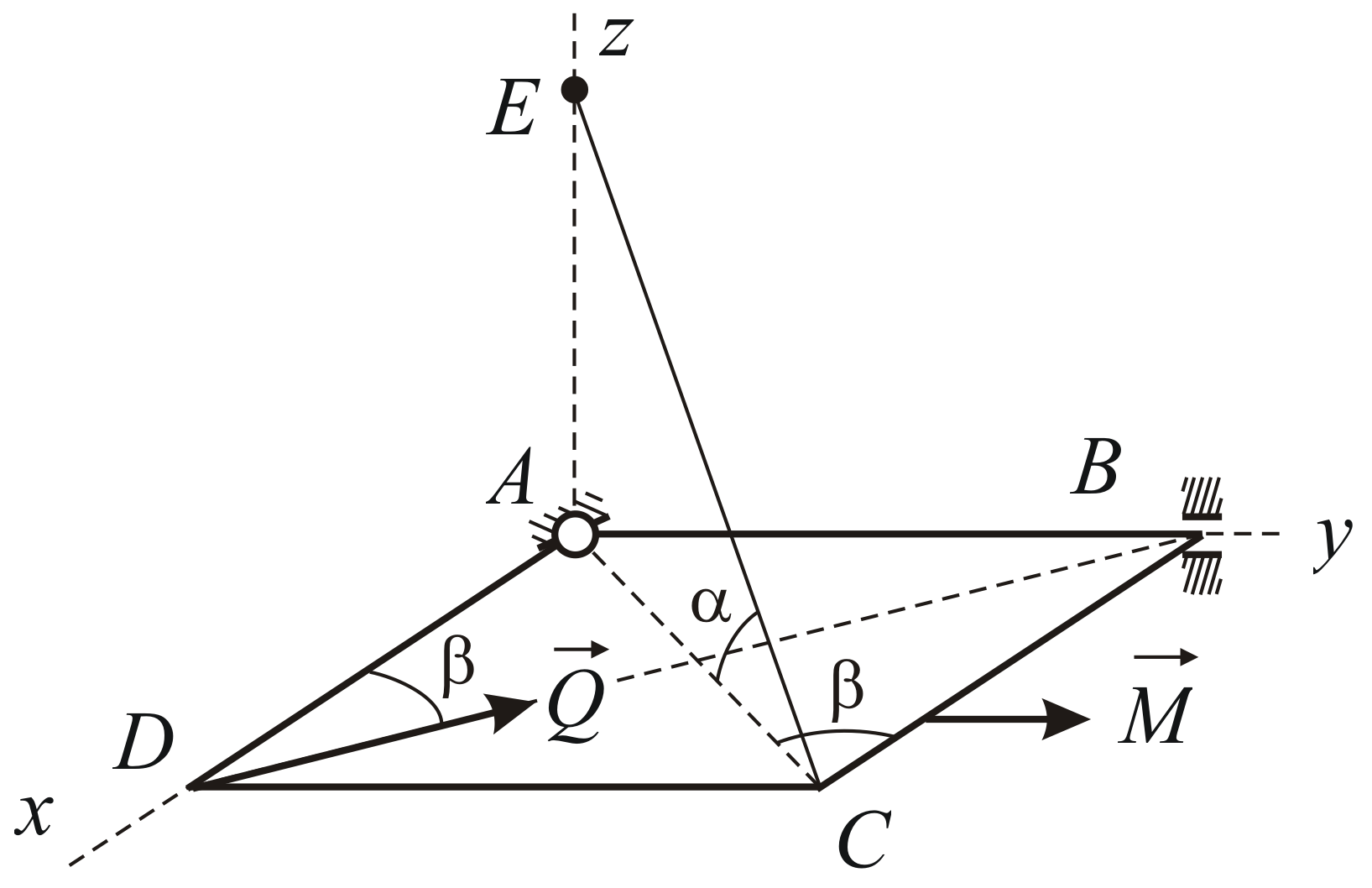
Однородная прямоугольная пластина весом удерживается в горизонтальном положении при помощи шарового шарнира, цилиндрического шарнираи троса(Рис. 4.6). На пластину действуют силаи пара сил с моментом. Даны размеры пластины и угол. Определить реакции опор.

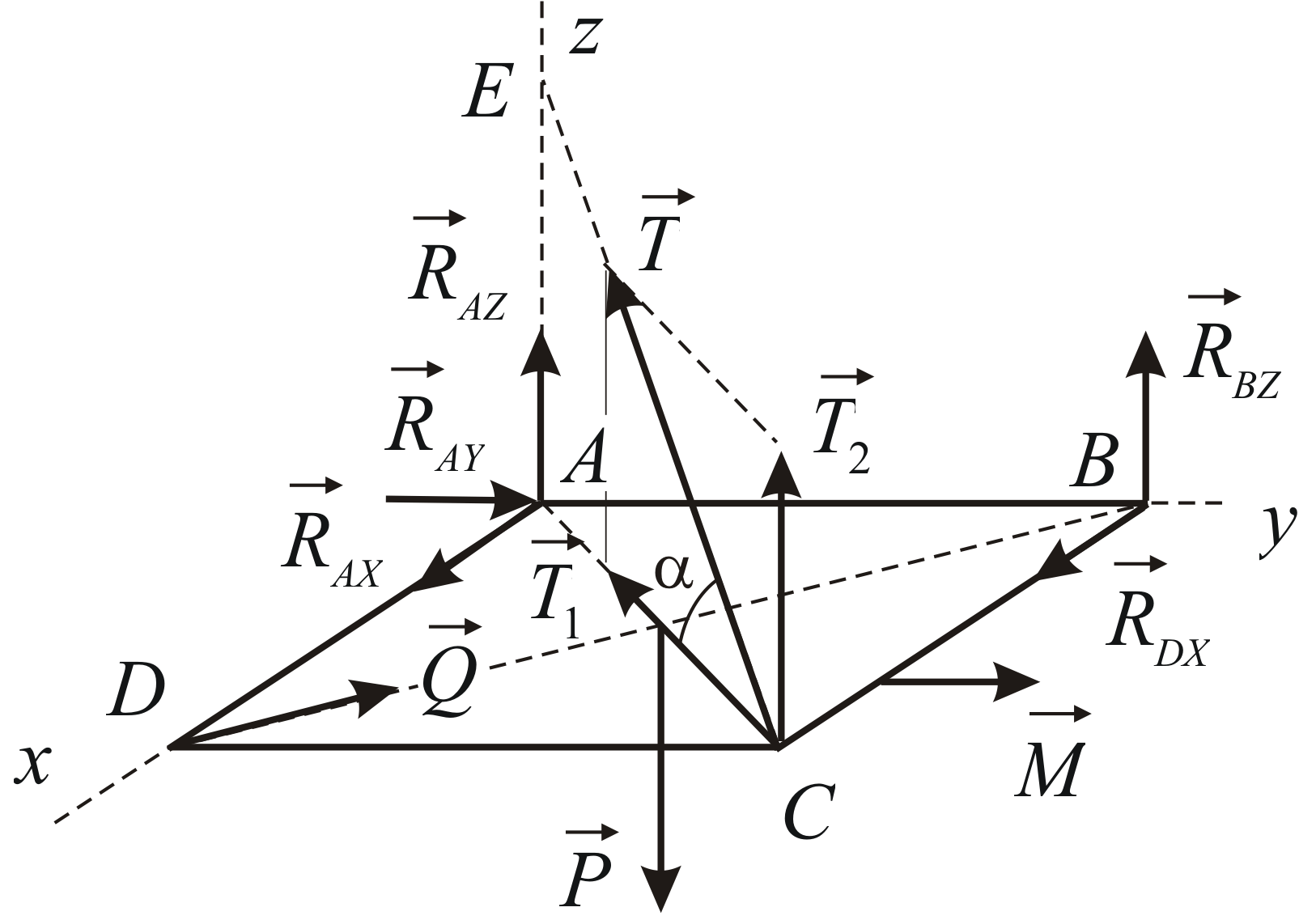
Рассмотрим равновесие пластины. Силовая расчётная схема представлена на Рис. 4.7. Сила реакции троса разложена на две составляющие:; (), линия действия которой проходит через начало координат, и; (), линия действия которой параллельна оси.

Рис. 4.6		Рис. 4.7

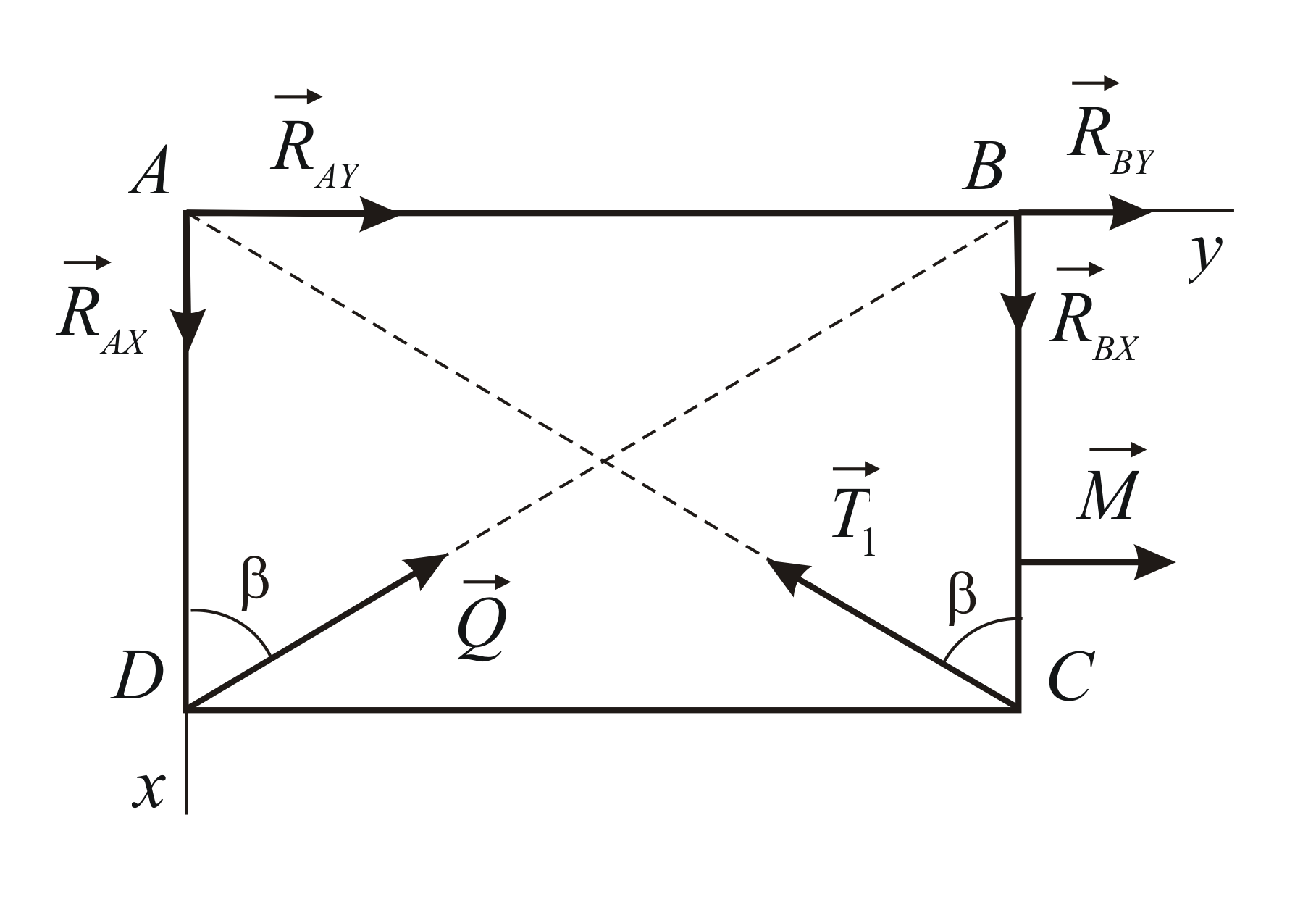
Заметим, что линия действия силы пересекает все три координатные оси и, следовательно, не создаёт момента относительно любой из осей координат. Пара сил в данном случае создаёт вращающий момент относительно оси, параллельно которой располагается вектор.

Рис. 4.8

Угол(точнее значения тригонометрических функций этого угла) легко вычислить через заданные длины сторон пластины (Рис. 4.8):

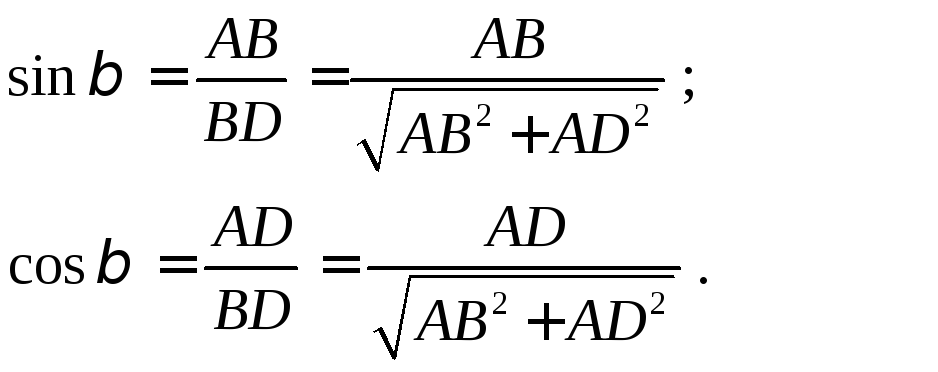
Условия равновесия имеют вид:

Полученная система уравнений позволяет определить все неизвестные величины.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Как вычисляется момент силы относительно оси?

2. Как вычисляется сумма моментов относительно оси сил, образующих пару сил?

3. При каких условиях момент силы относительно оси равен нулю?

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 8.13; 8.14; 8.15; 8.16; 8.18; 8.19; 8.21; 8.22; 8.23; 8.24; 8.25; 8.26.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-4

КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ:

1. После практического занятия №3 проводится тест «МОДУЛЬ СТ-1».

2. После практического занятия №8 проводится тест «МОДУЛЬ СТ-2».

ЛИТЕРАТУРА:

1. Антонов В.И., Белов В.А., Егорычев О.О., Степанов Р.Н.//Курс теоретической механики (теория и практика) – М.: Архитектура – С, 2011 г.

2. Мещерский И.В.//Сборник задач по теоретической механике. – Спб.: Лань, 2010 г.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1(9)