1.6. Распределённая нагрузка

Поверхностные и объёмные силы представляют собой нагрузку, распределённую по некоторой поверхности или объёму. Такая нагрузка задаётся интенсивностью , которая представляет собой силу, приходящуюся на единицу некоторого объёма, или некоторой площади, или некоторой длины.

Особое место при решении ряда практически интересных задач занимает случай плоской распределённой нагрузки, приложенной по нормали к некоторой балке. Если вдоль балки направить ось , то интенсивность будет функцией координаты и измеряется в Н/м. Интенсивность представляет собой силу, приходящуюся на единицу длины.

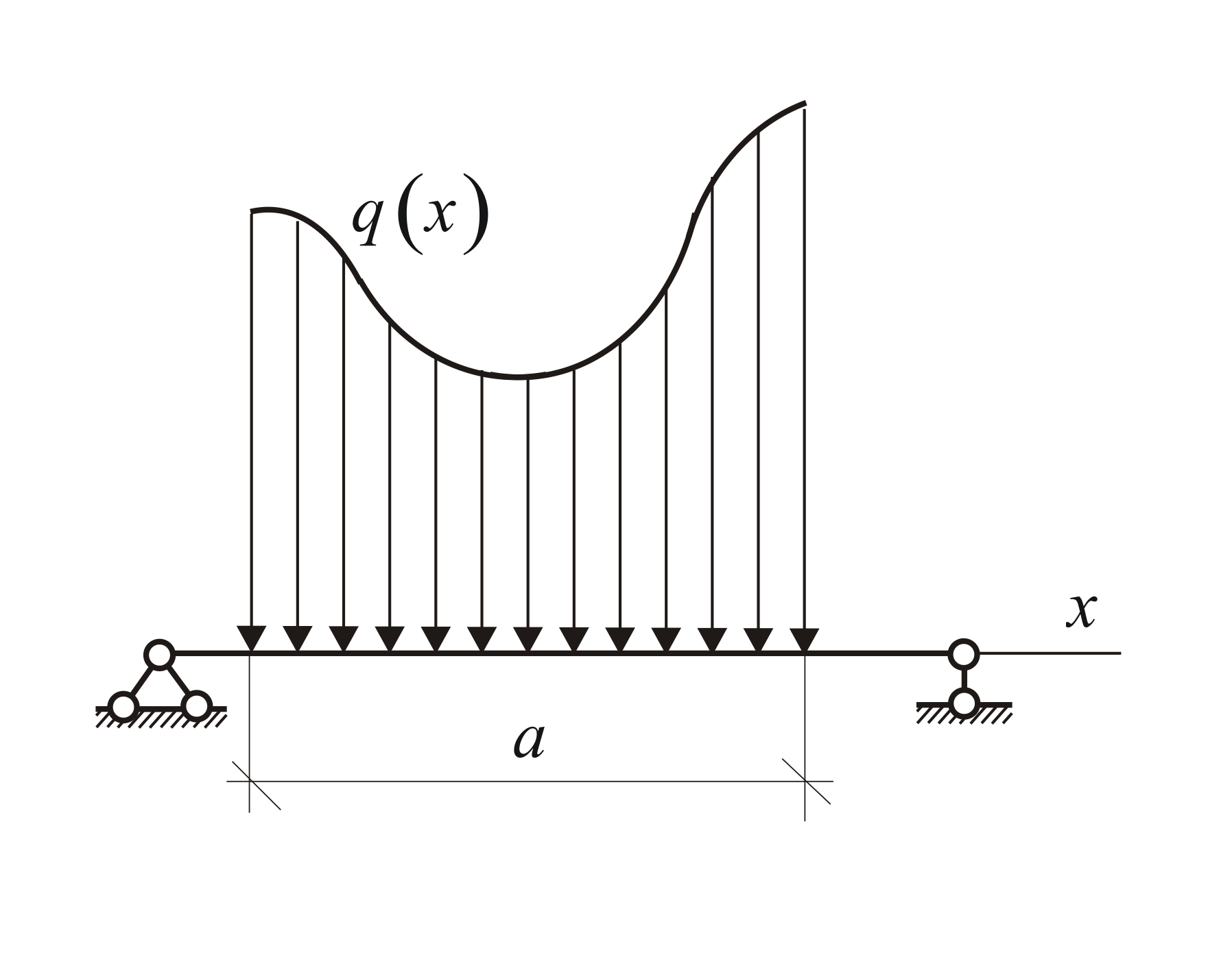
Плоская фигура, ограниченная балкой и графиком интенсивности нагрузки, называется эпюрой распределённой нагрузки (Рис. 1.28). Если по характеру решаемой задачи можно не учитывать деформации, т.е. можно считать тело абсолютно твёрдым, то распределённую нагрузку можно (и нужно) заменить равнодействующей.

Рис. 1.28		Рис. 1.29

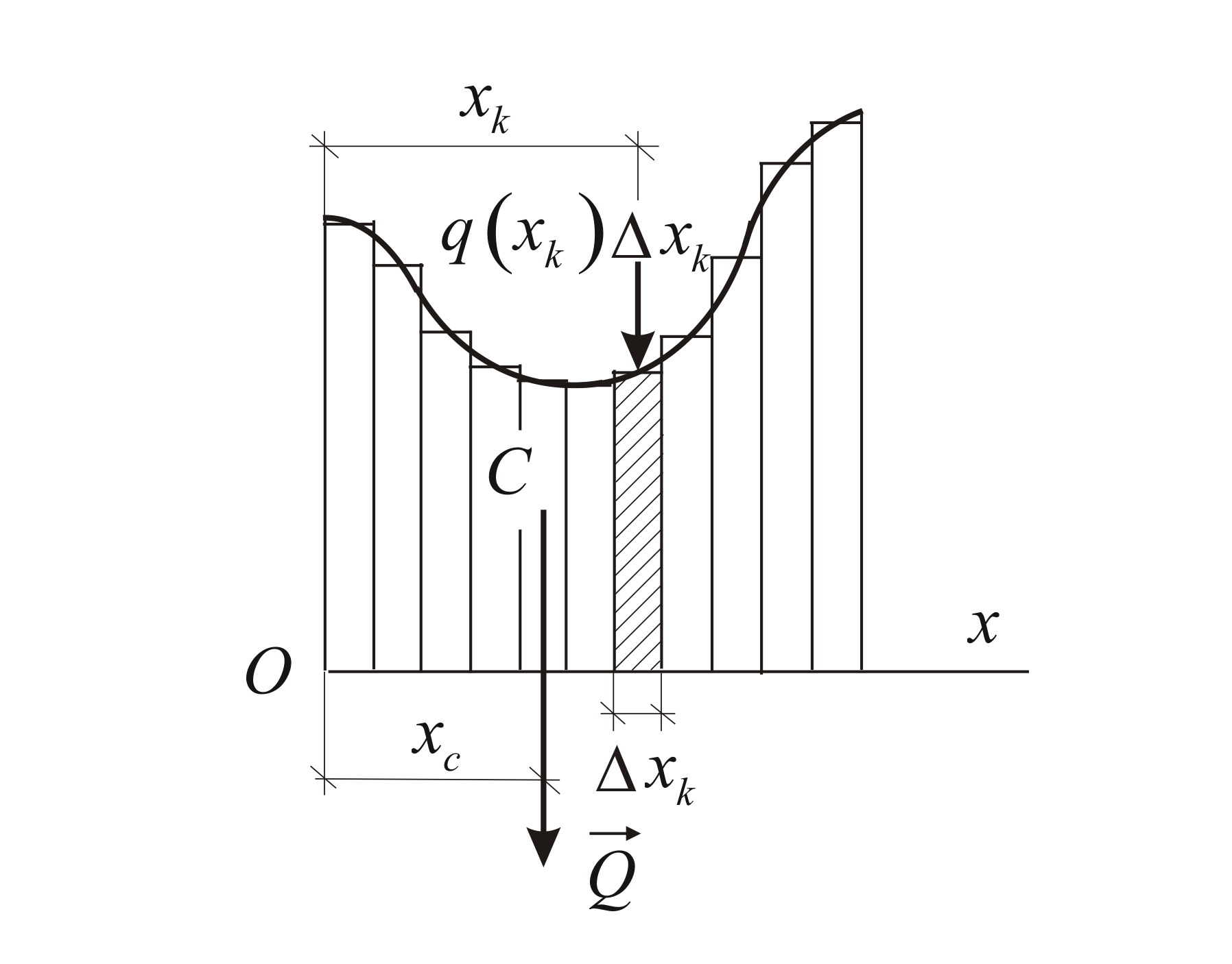
Разобьём балку на отрезков длиной , на каждом из которых будем считать интенсивность постоянной и равной , где –координата отрезка . При этом кривая интенсивности заменяется ломаной линией, а нагрузка, приходящаяся на отрезок , заменяется сосредоточенной силой , приложенной в точке (Рис. 1.29). Полученная система параллельных сил имеет равнодействующую, равную сумме сил, действующих на каждый из отрезков, приложенную в центре параллельных сил.

Понятно, что такое представление тем точнее описывает реальную ситуацию, чем меньше отрезок , т.е. чем больше число отрезков . Точный результат получаем, переходя к пределу при длине отрезка , стремящейся к нулю. Предел, получаемый в результате описанной процедуры, представляет собой интеграл. Таким образом, для модуля равнодействующей получаем:

Для определения координаты точки приложения равнодействующей используем теорему Вариньона:

если система сил имеет равнодействующую, то момент равнодействующей относительно любого центра (любой оси) равен сумме моментов всех сил системы относительно этого центра (этой оси)

Записывая эту теорему для системы сил в проекциях на ось и переходя к пределу при длине отрезков, стремящейся к нулю, получаем:

Очевидно, модуль равнодействующей численно равен площади эпюры распределённой нагрузки, а точка её приложения совпадает с центром тяжести однородной пластины, имеющей форму эпюры распределённой нагрузки.

Отметим два часто встречающихся случая.

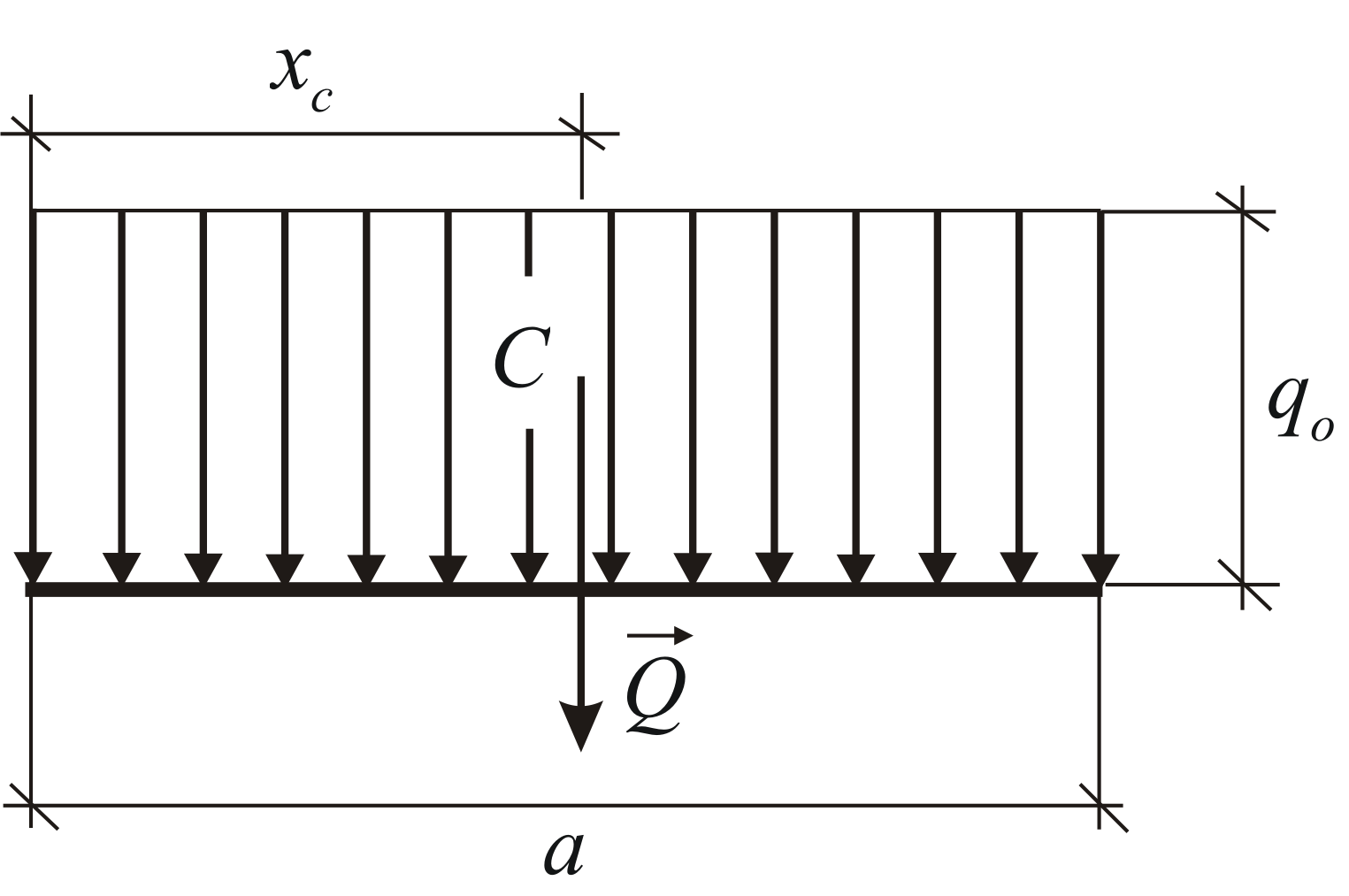
Равномерно распределённая нагрузка,(Рис. 1.30). Модуль равнодействующей и координата её точки приложения определяются по формулам:

В инженерной практике такая нагрузка встречается довольно часто. Равномерно распределённой в большинстве случаев можно считать весовую и ветровую нагрузку.

Рис. 1.30		Рис. 1.31

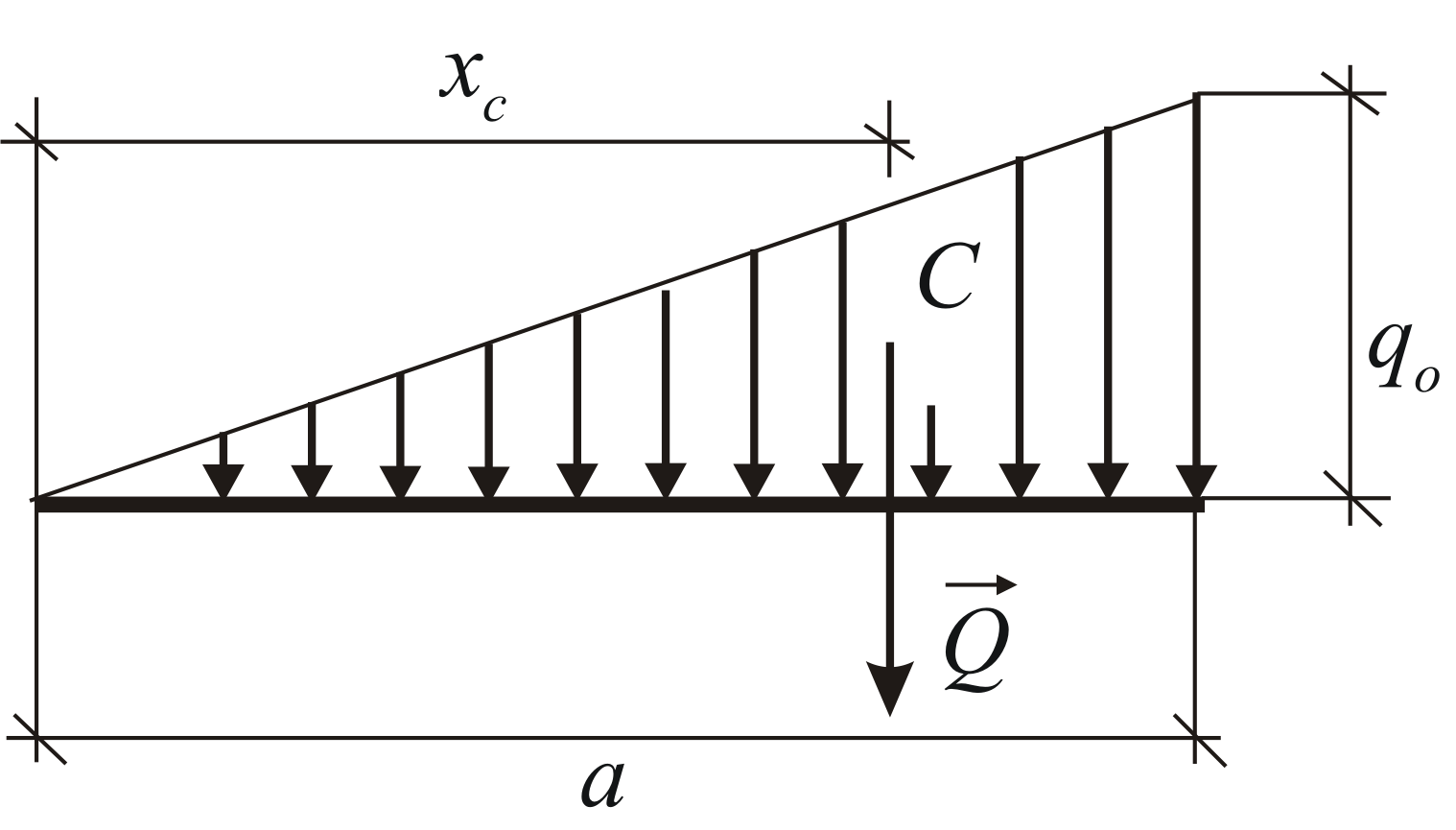
Линейно распределённая нагрузка,(Рис. 1.31). В этом случае:

В частности, давление воды на вертикальную стенку прямо пропорционально глубине .

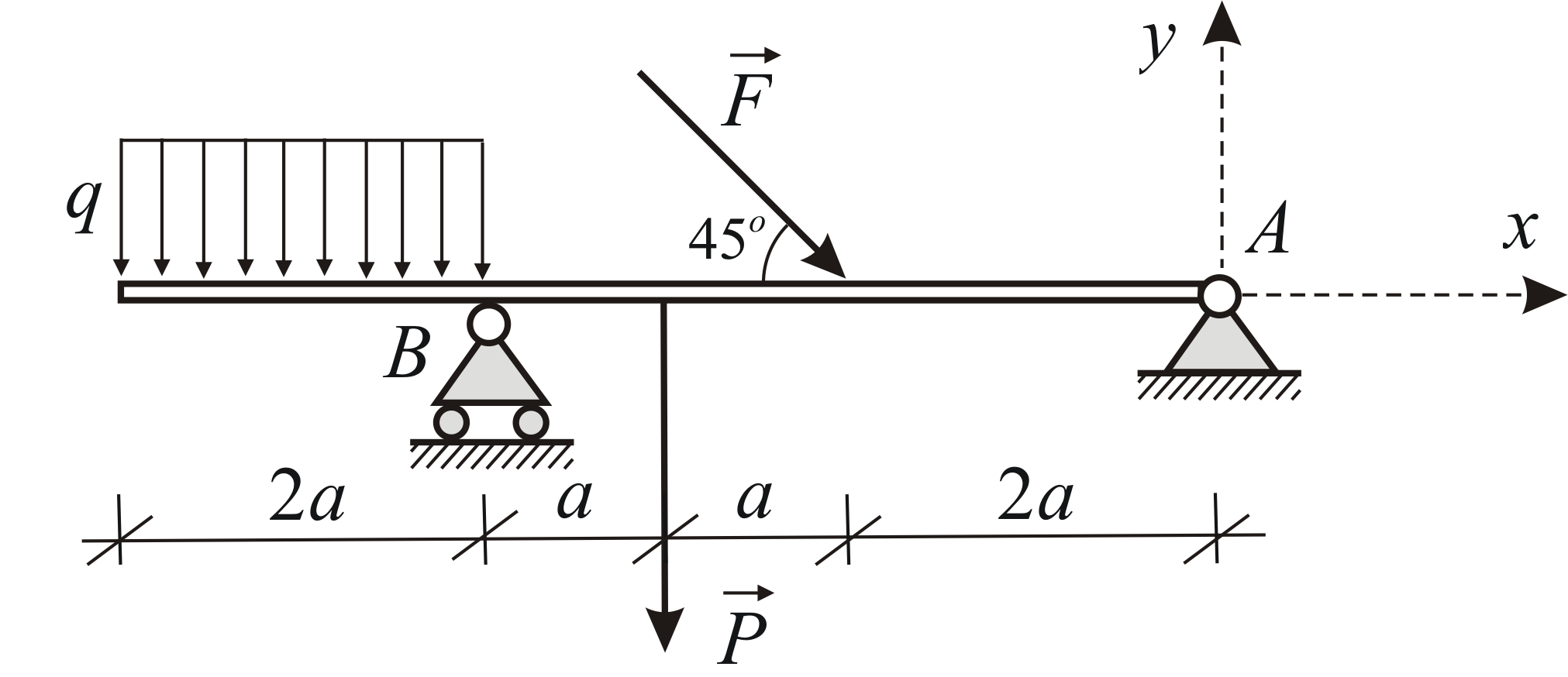
Пример 1.5

Определить реакции опор ибалки, находящейся под действием двух сосредоточенных сил и равномерно распределённой нагрузки. Дано:

Рис. 1.32

Найдём равнодействующую распределённой нагрузки. Модуль равнодействующей равен

плечо силы относительно точкиравноРассмотрим равновесие балки. Силовая схема представлена на Рис. 1.33.

Рис. 1.33

Условия равновесия в рассматриваемом случае имеют вид:

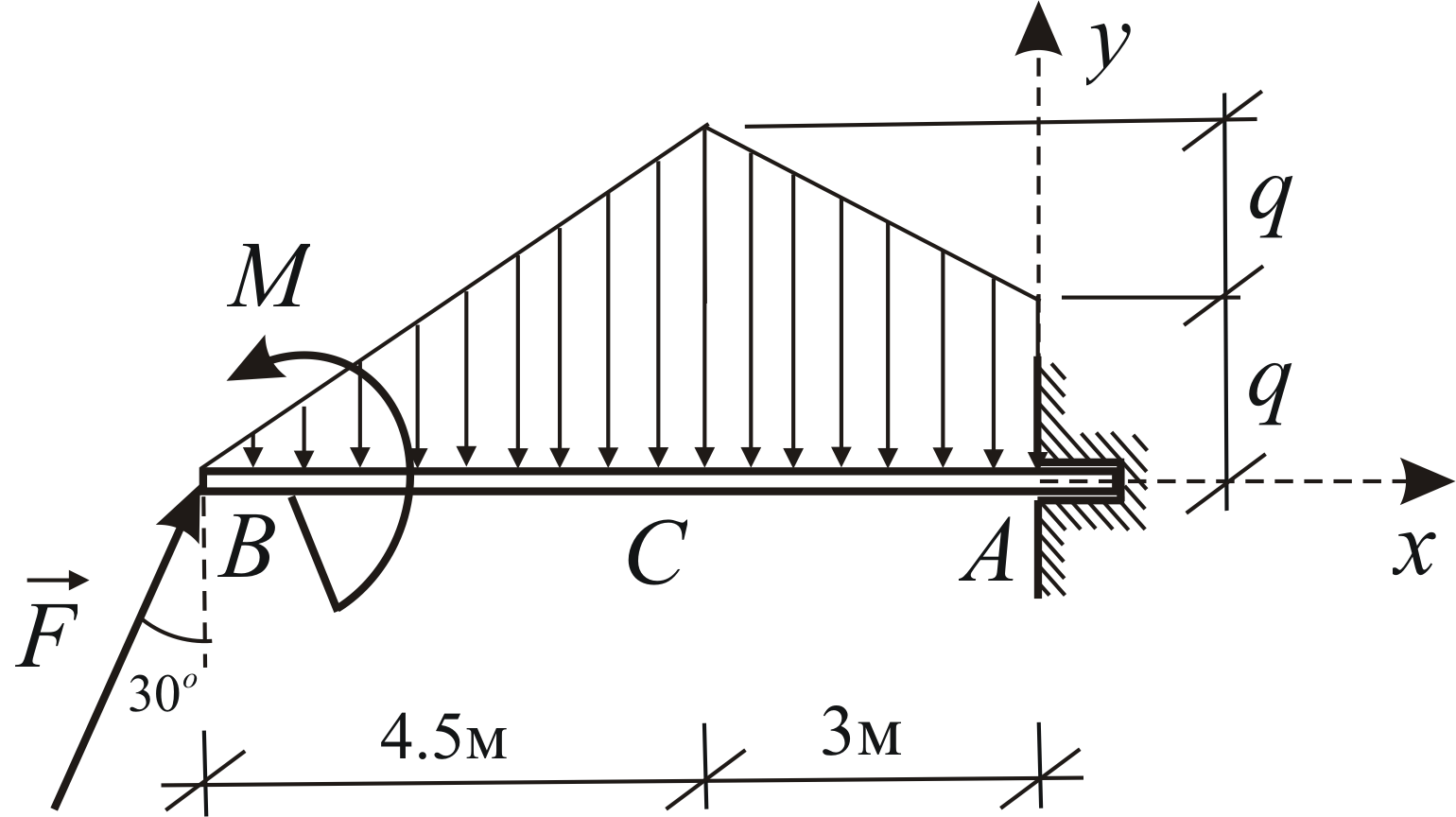
Пример 1.6

Определить реакцию заделки консольной балки, находящейся под действием сосредоточенной силы, пары сил и распределённой нагрузки (Рис. 1.34).

Дано:

Заменим распределённую нагрузку тремя сосредоточенными силами. Для этого разобъём эпюру распределённой нагрузки на два треугольника и прямоугольник. Находим

Силовая схема представлена на Рис. 1.35.

Рис. 1.34		Рис. 1.35

Вычислим плечи равнодействующих относительно оси

Условия равновесия в рассматриваемом случае имеют вид:

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Что называется интенсивностью распределённой нагрузки?

2. Как вычислить модуль равнодействующей распределённой нагрузки?

3. Как вычислить координату точки приложения равнодействующей распределённой

нагрузки?

4. Чему равен модуль и какова координата точки приложения равномерно распределённой нагрузки?

5. Чему равен модуль и какова координата точки приложения линейно распределённой нагрузки?

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 4.28; 4.29; 4.30; 4.33; 4.34.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-2; СР-3.

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 4-5