1.4. Учёт пары сил при составлении уравнений равновесия

Рассмотрим особенности решения задач, в которых наряду с силами на тело действует пара сил с моментом, расположенная в координатной плоскости.

При составлении уравнений равновесия следует учитывать, что в условия равенства нулю суммы проекций всех сил на любую координатную ось входящие в пару силы иникакого вклада не внесут, так как сумма проекций этих сил на любую координатную ось равна нулю ().

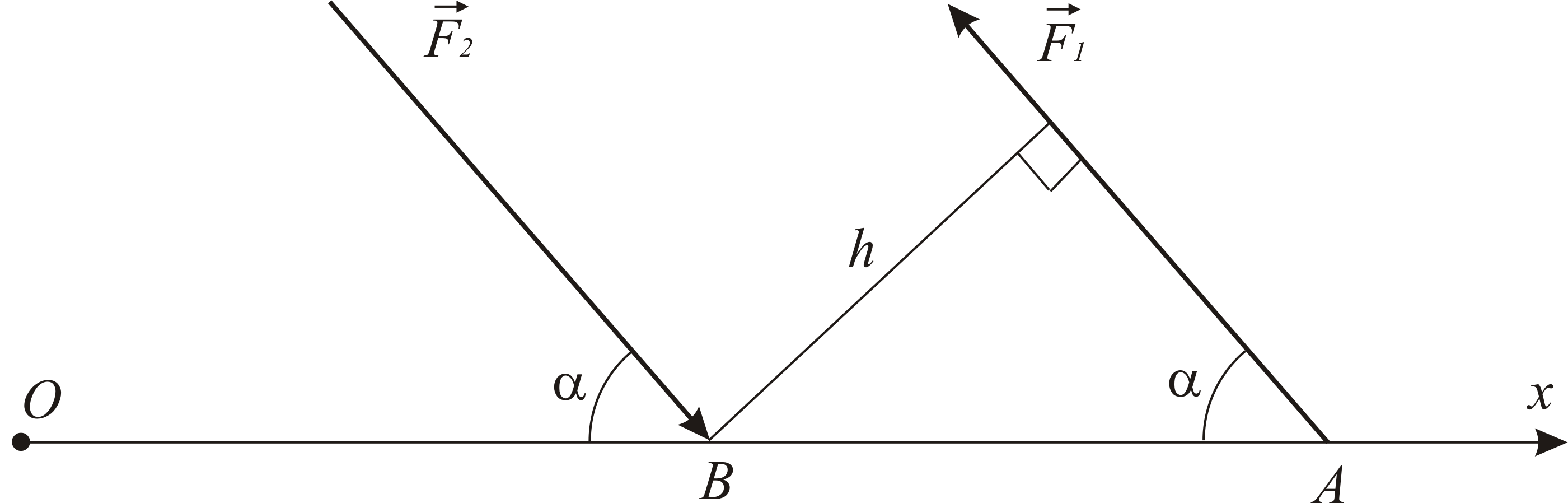
Вычислим сумму моментов сил, образующих пару, относительно оси (Рис. 1.21).

Рис. 1.21

Таким образом, в уравнении моментов к моментам прочих сил алгебраически прибавляется момент пары, точнее проекция на ось вектора момента пары, взятая с соответствующим знаком. Проекция момента пары положительна, если с положительного конца осиповорот пары виден против хода часовой стрелки.

Пример 1.3

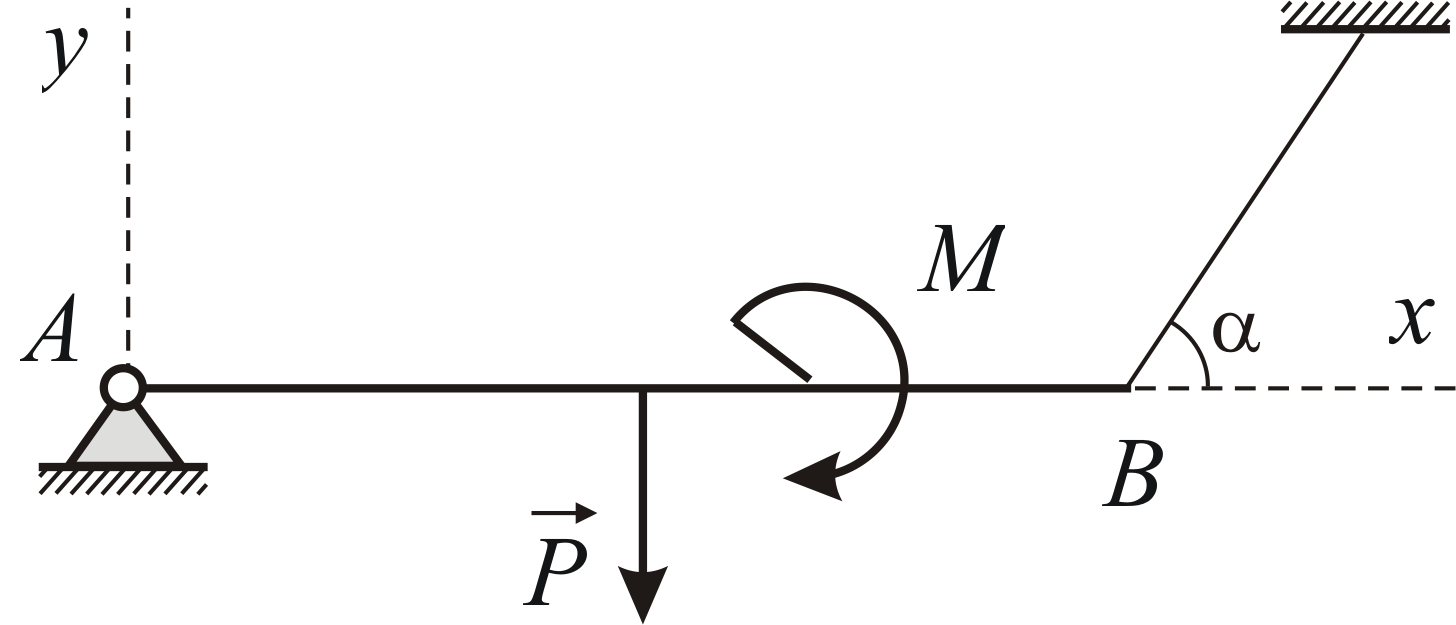
Однородная балка весом, шарнирно закреплённая в точке, удерживается в горизонтальном положении при помощи троса. Балка нагружена парой сил с моментом(Рис. 1.22). Дано:Н;Нм;м;. Определить давление на шарнири натяжение троса.

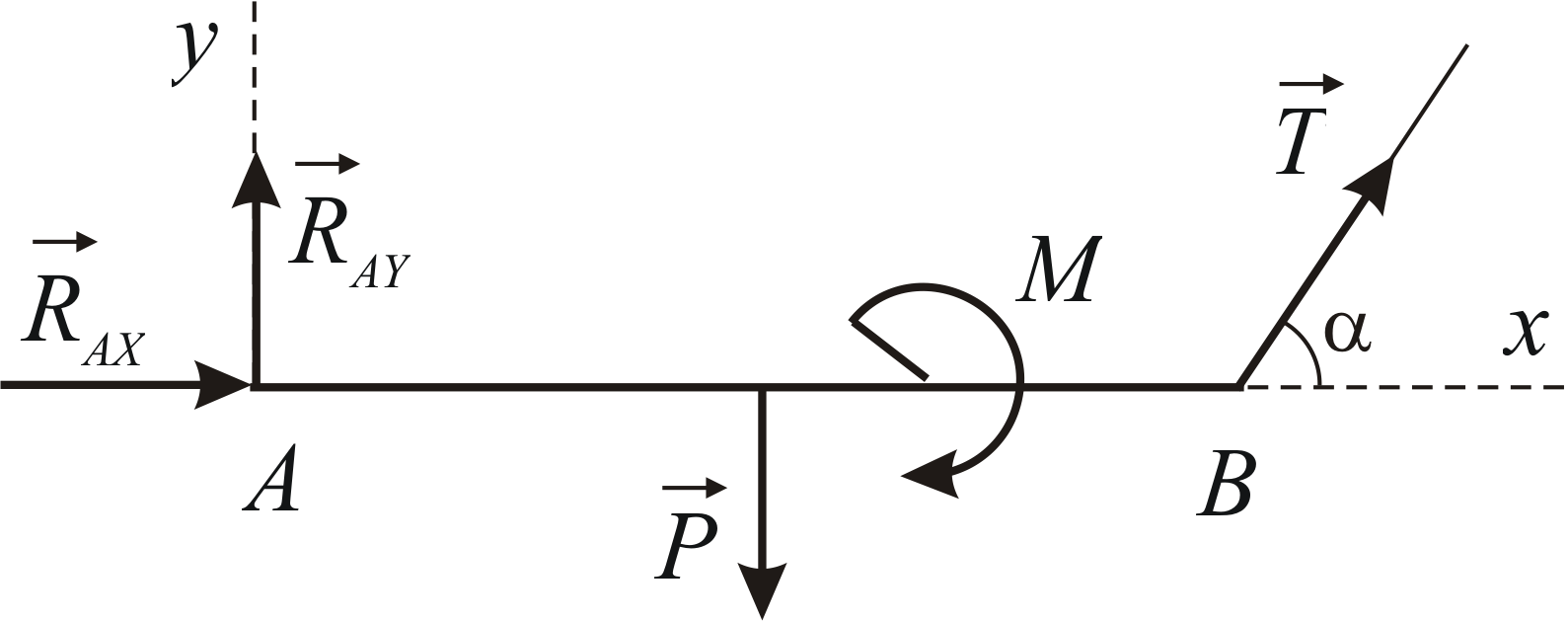
Рассмотрим равновесие балки . Силовая схема представлена на Рис. 1.23. Заметим, что необходимо определить силы, приложенные не к балке, а к другим телам – шарниру и тросу. Мы рассматриваем равновесие балки и поэтому ввели силы реакции шарнираи реакции троса. Но эти реакции, согласно третьему закону Ньютона, равны по модулю и противоположны по направлению искомым силам.

Рис. 1.22		Рис. 1.23

При составлении уравнения моментов за моментную примем точку и заметим, что поворот, создаваемый парой сил, виден по ходу часовой стрелки.

Отсюда:

Н;Н;Н.

Давление на шарнир определим по формуле:

Н.

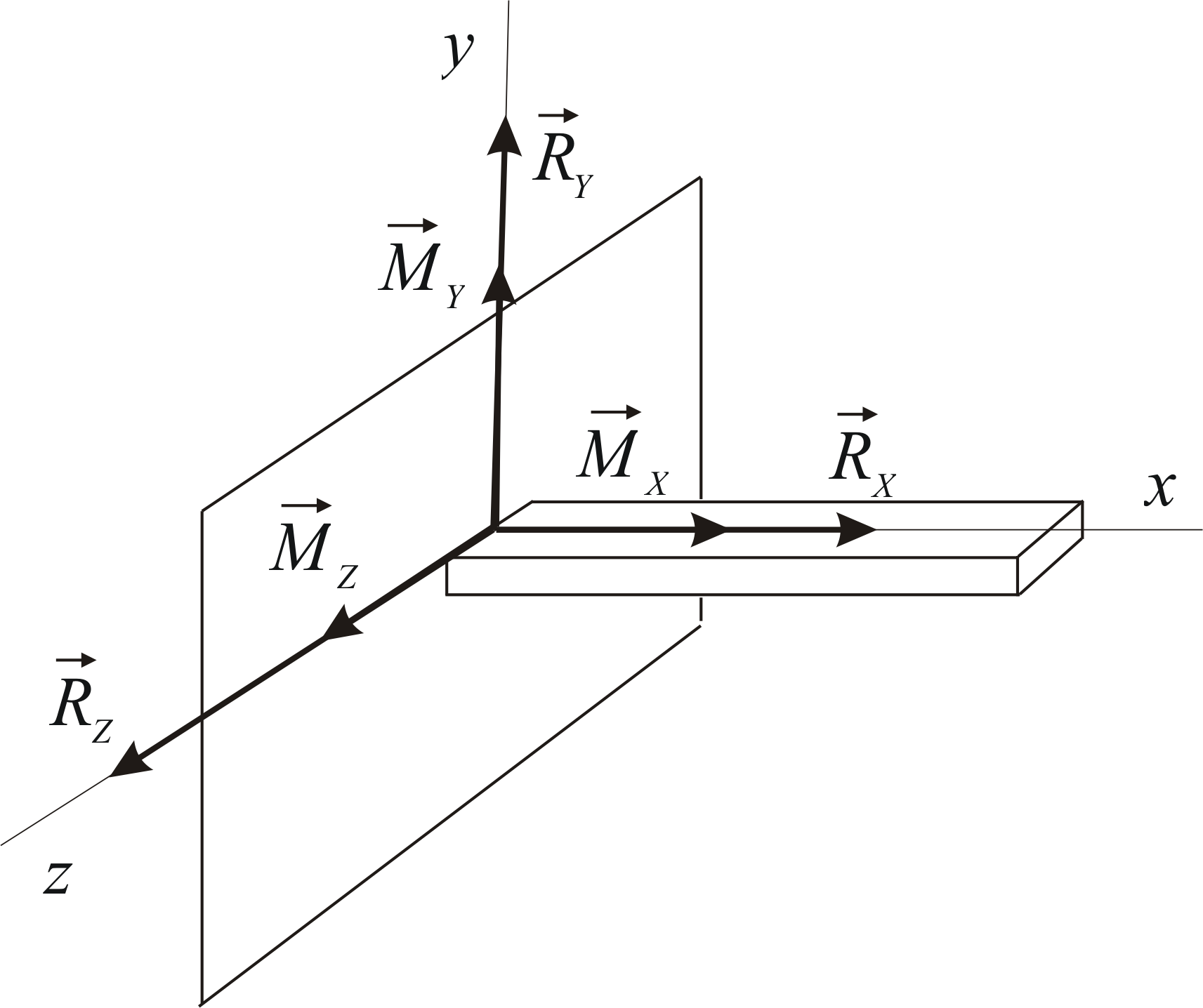
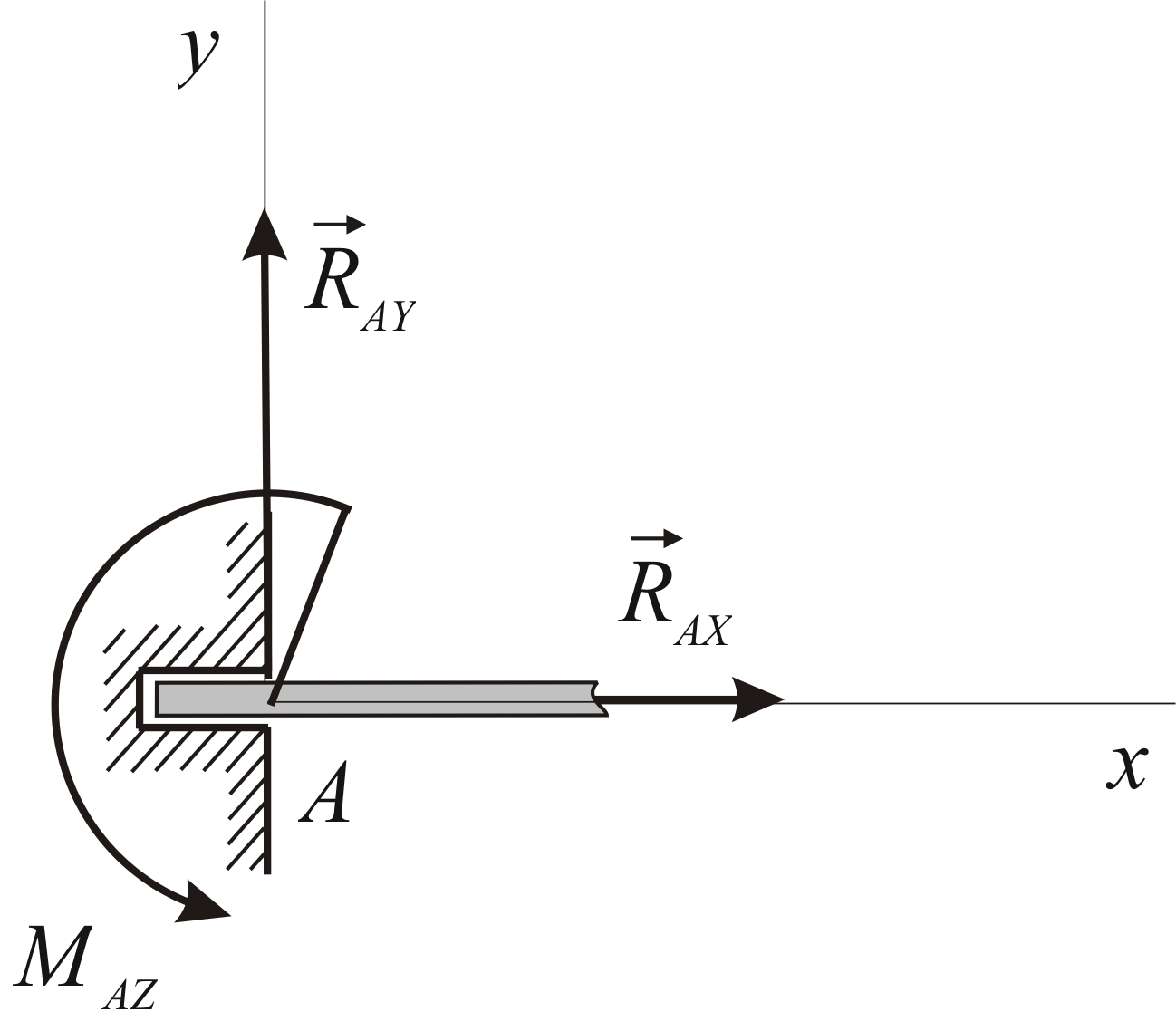
0. Жёсткая заделка.

Рассмотрим балку, один конец которой заделан в стену (Рис. 1.24). Подобно неподвижному шарниру, жёсткая заделка препятствует любым перемещениям конца балки и, следовательно, создаёт неизвестную по модулю и направлению силу реакции. Но в отличие от шарнира, заделка препятствует любым поворотам балки, создавая кроме силы реакции ещё и пару сил, направление и модуль момента которой заранее неизвестны. Таким образом, в общем случае получаем в качестве неизвестных три проекции силы реакции на координатные оси и три момента реакции относительно координатных осей.

Рис. 1.24		Рис. 1.25

Особый интерес представляет случай, когда система активных сил расположена в одной плоскости (например, в координатной плоскости . В этом случае система сил реакций также будет плоской и реакция заделки будет представлена двумя составляющими силыии одной составляющей момента(Рис. 1.25). Неизвестными величинами в таком случае будут проекции этих составляющих на соответствующие координатные оси.

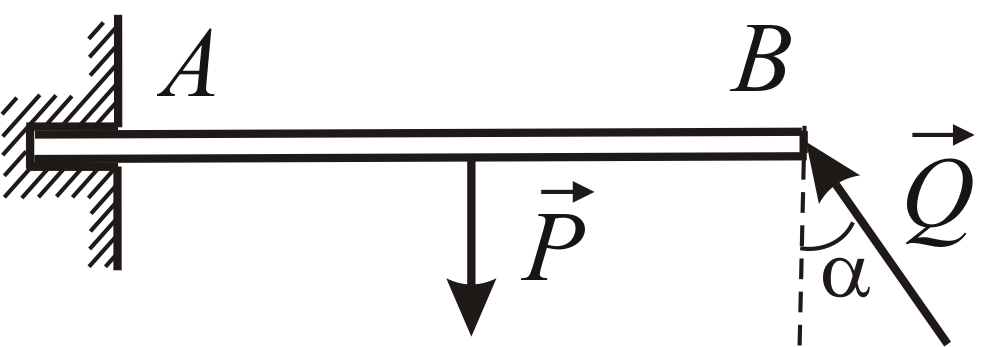
Пример 1.4

Однородная балка весом, защемлена в стене в сечении. Балка нагружена силой, приложенной в точке(Рис. 1.26). Определить составляющие реакции заделки.

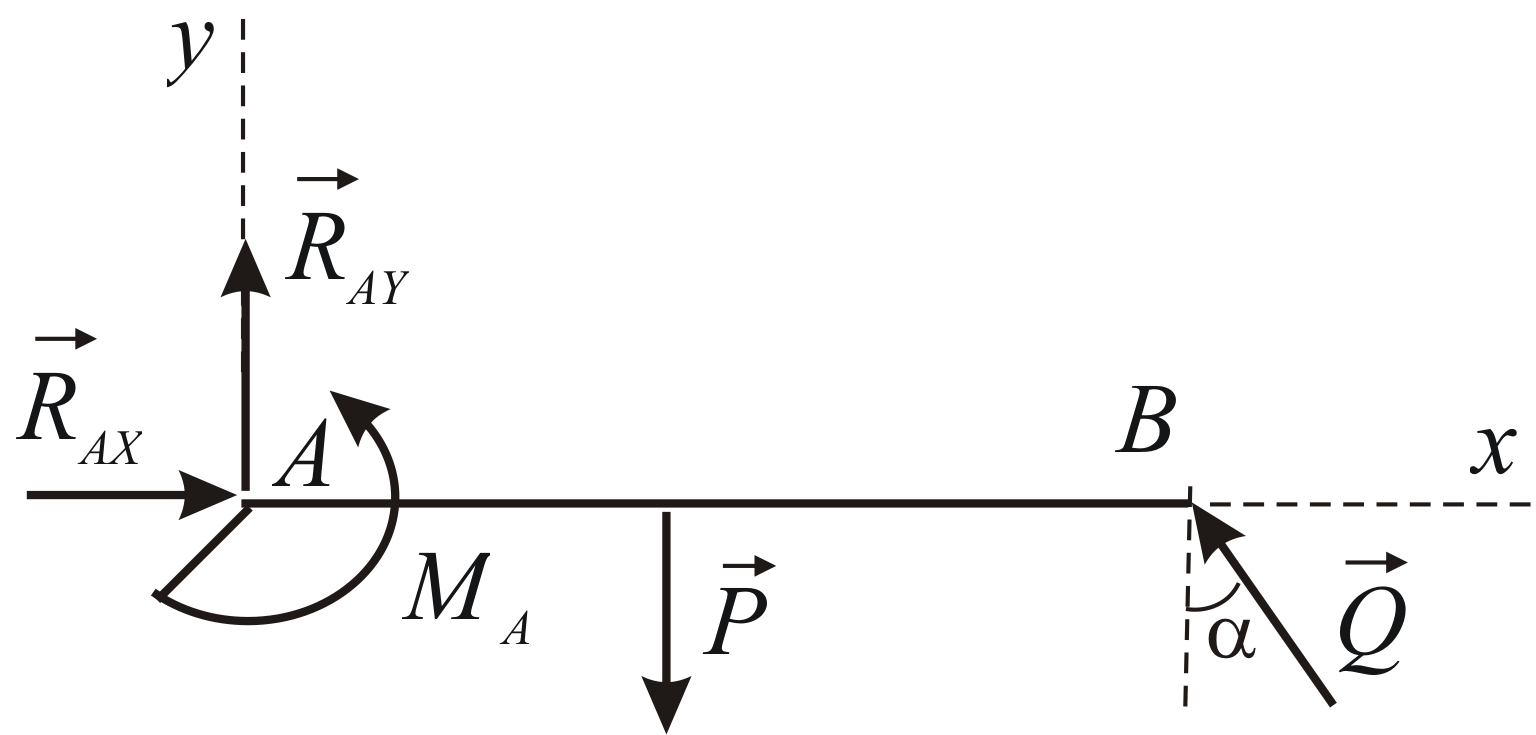
Рис. 1.26		Рис. 1.27

Рассмотрим равновесие балки . Силовая схема представлена на Рис. 1.27.

Условия равновесия имеют вид:

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Какой вклад вносит пара сил в уравнения равновесия?

2. Какими составляющими представляется реакция жёсткой заделки?

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 4.25; 4.27.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-2; СР-3

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3